Chapter 4 | Trees and Graphs--判断有向图两节点之间是否存在路径

4.2  Given a directed graph, design an algorithm to find out whether thereis a route between two nodes.

译文：给定一个有向图，设计一个算法判断两节点之间是否存在路径。

这个题目实际上就是考察图的遍历，前面已经介绍了图的两种遍历方式：BFS和DFS 。这里判断两个节点之间是否存在路径，实质就是给定一个开始顶点，然后判断能否遍历到另一个指定顶点。这种情况下，我们采用BFS遍历判断。

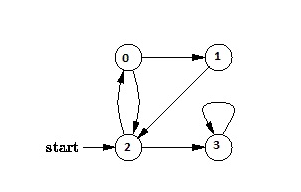
先构建一个有向图（前面我们构建的都是无向图）

                                    

#include <iostream>
#include <list>

using namespace std;

class graph
{
public:
	graph(int v) :vertex(v){
		adj = new list<int>[v];
	}

	void addEdge(int v, int w);
	bool BFS(int vStart, int vEnd);

private:
	int vertex;
	list<int> *adj;
};

//v:边的首顶点；w：边的尾顶点
void graph::addEdge(int v, int w)
{
	adj[v].push_back(w);
}

构建有向图：

int main()
{
    graph g(4);
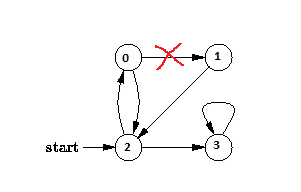
    g.addEdge(0, 1);//注释该行，构建的有向图如第二图所示
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    if (g.BFS(2, 1))
        cout << "yes" << endl;
    else
        cout << "no" << endl;

    return 0;
}

BFS

bool graph::BFS(int vStart, int vEnd)
{
	bool *visited = new bool[vertex];
	memset(visited, false, vertex);

	list<int> queue;//利用链表构建一个队列

	visited[vStart] = true;//表示开始访问
	queue.push_back(vStart);//开始顶点入队

	list<int>::iterator iter;

	//队列中的顶点就是访问的顶点
	while (!queue.empty())
	{
		vStart = queue.front();//这里有个优先级，邻接表中链表的头节点优先级最高，依次降低
		queue.pop_front();//已访问顶点出队

		if (vStart == vEnd)//如果已访问的顶点恰好是指定目的顶点则表明有路径
			return true;

		//将与开始顶点最近的顶点，也就是链表中的顶点依次入队
		for (iter = adj[vStart].begin(); iter != adj[vStart].end(); ++iter)
		{
			if (!visited[*iter])
			{
				visited[*iter] = true;//标记即将访问，事实上，进入队列了就是要访问的
				queue.push_back(*iter);//从链表头节点到尾节点依次入队
			}
		}
	}
	return false;
}