文法的定义
一个文法G是一个四元组:G(,
,S,P)
:一个非空有限的终极符号集合。它的每个元素称为终极符号或终极符,一般用小写字母表示。终极符号是一个语言不可再分的基本符号。
:一个非空有限的非终极符号集合。它的每个元素称为非终极符号或非终极符,一般用大写字母表示。
V是文法G的符号集,则V=
∪
,
∩
=
S:一个特殊的非终极符号,称为文法的开始符号或识别符号,。开始符号S必须至少在某个产生式的左部出现一次。
P:产生式的有限集合。
产生式:也成为产生规则或简称为规则
产生式形式:α->β等,其中α称为产生式的左部,α
,并且至少含有一个非终极符;β称为产生式的右部,β
;->或::=读作定义为或由...组成。
(α是由β组成的)

文法分类
0型文法(短语型文法)
设文法G(,
,S,P),如果对P中每一条产生式α->β不加限制,即
,并且至少有一个非终极符,
,则称G为0型文法或短语型文法。
1型文法(上下文相关文法)
设文法G(,
,S,P),除
且S不出现在任何产生式的右侧外,如果对P中的每条产生式均限制为形如
其中,,
,
,则称文法G为1型文法或上下文相关文法。
这种文法意味着,终极符A只有在α和β这样的一个上下文环境中才可以被替换为γ,显示了上下文相关的特点。
2型文法(上下文无关文法)
设文法G(,
,S,P),如果对P中的每条产生式均限制为形如
其中,,
,则称G为2型文法或上下文无关文法。
在2型文法中,用α取代非终极符A,与A所在上下文无关,所以称之为上下文无关文法。
3型文法(线性文法、正则文法或正规文法)
设文法G(,
,S,P),如果对P中的每条产生式均限制为形如
或
其中,,
,则称G为3型文法。
上述形式的3型文法也称为右线性文法,3型文法还有另一种形式,称为左线性文法。如果对文法G的每条产生式形如或
其中,
,称该3型文法为左线性文法。
上述四类文法,从0型文法到3型文法,对产生式的限制是逐步增强的,而描述语言的能力是逐步减弱,其后一类都是前一类的子集。四类文法之间的关系可以表示为:
0型文法
1型文法
2型文法
3型文法
对于每一型文法,都有一类自动机和它的描述能力等价,对应关系如下:
0型文法对应图灵机(TM)
1型文法对应线性有界自动机(LBA)
2型文法对应下推自动机(PDA)
3型文法对应有限自动机(FA)
在编译技术中通常用3型文法来描述高级程序设计语言的词法部分,然后用有限自动机FA来识别高级语言的单词。今后对“文法”一词如无特殊说明则均指上下文无关文法。
总结:(直接看长得像不像)
0型文法:α->β
1型文法:
2型文法:
(左部只有一个非终极符,右部终极符和非终极符)
3型文法:
或
、
或
(产生式的右部至多有两个符号且满足下面的形式之一:
、
,其中
,
)
推导和归纳

1.直接推导

2.直接推导序列

3.最左推导
在推导过程中,总是对当前符号串中最左的非终极符进行替换,称为最左推导。
4.最右推导
在推导过程中,总是对当前符号串中最右的非终极符进行替换,称为最右推导。
5.句型

6.句子

显然。句子是句型的特例,只含有终极符的句型就是句子。文法G的句子的全体称为它所产生的语言,记作L(G)。
最右推导也称为规范推导。仅用规范推导得到的句型称为规范句型。规范推导的逆过程称为规范规约。
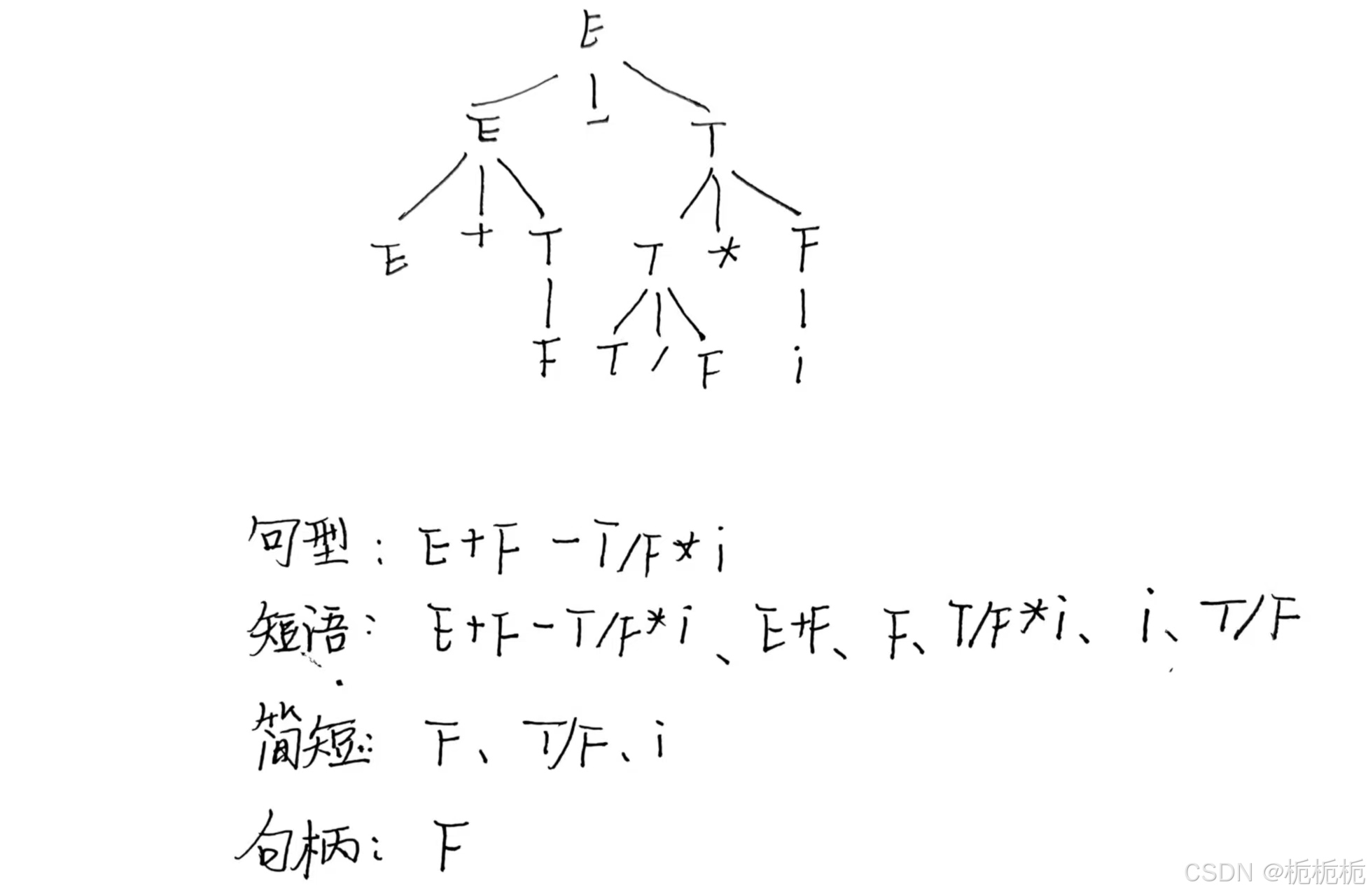
7.短语
一棵树及其子树包含的所有叶节点组成的符号串。
8.直接短语(简单短语)
只包含叶节点的子树,其叶节点组成的符号串。
9.句柄
最左端的简单短语。
题目:
语法树与文法二义性
前面介绍了句型、推导等概念。
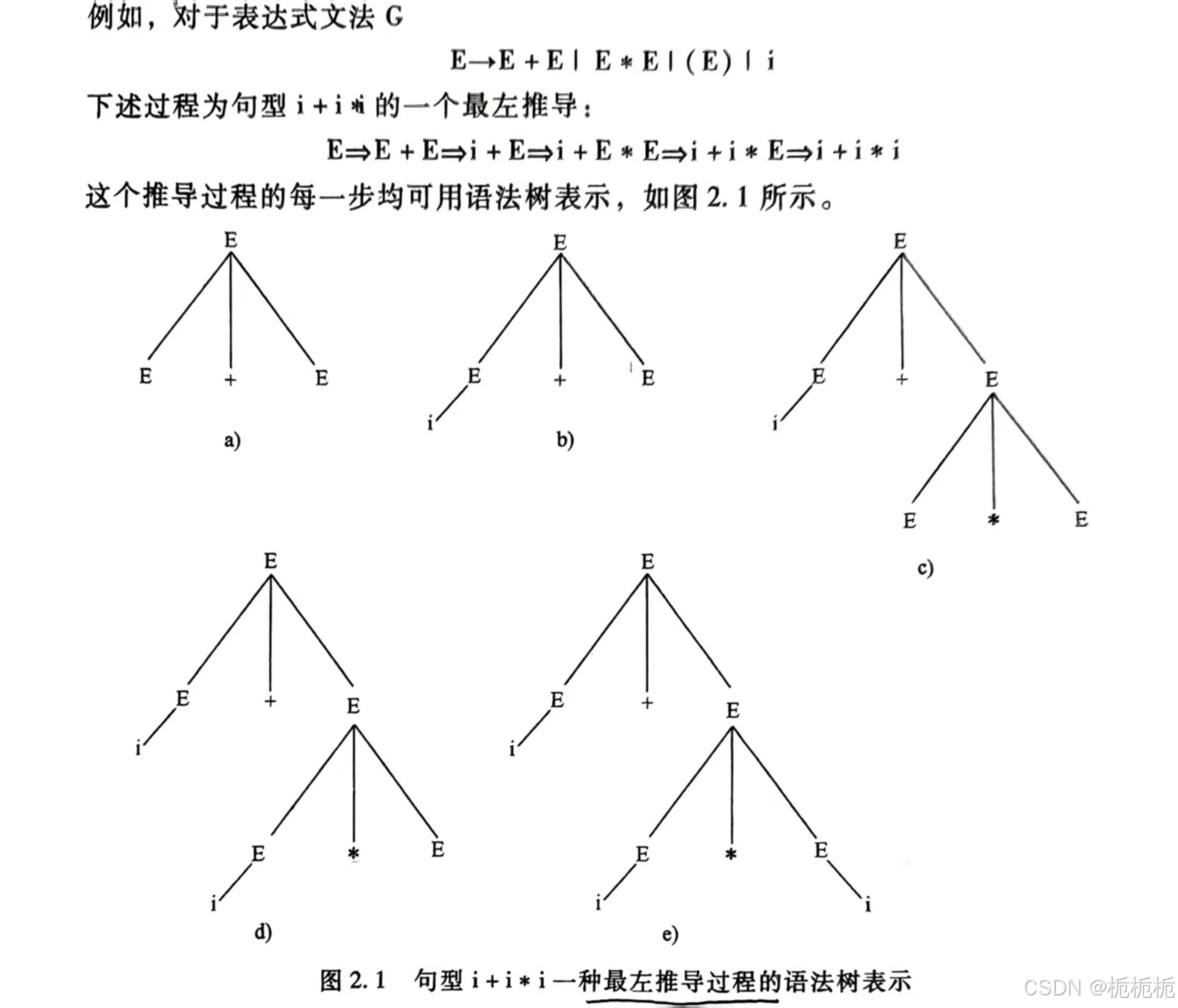
下面介绍一种上下文无关文法的句型推导过程的直观描述方法,即语法树(也称推导树、生成树、分析树)。
语法树


例:
最左推导👇
最右推导👇(树和e一样)
既非最左也非最右推导👇(树和e一样)
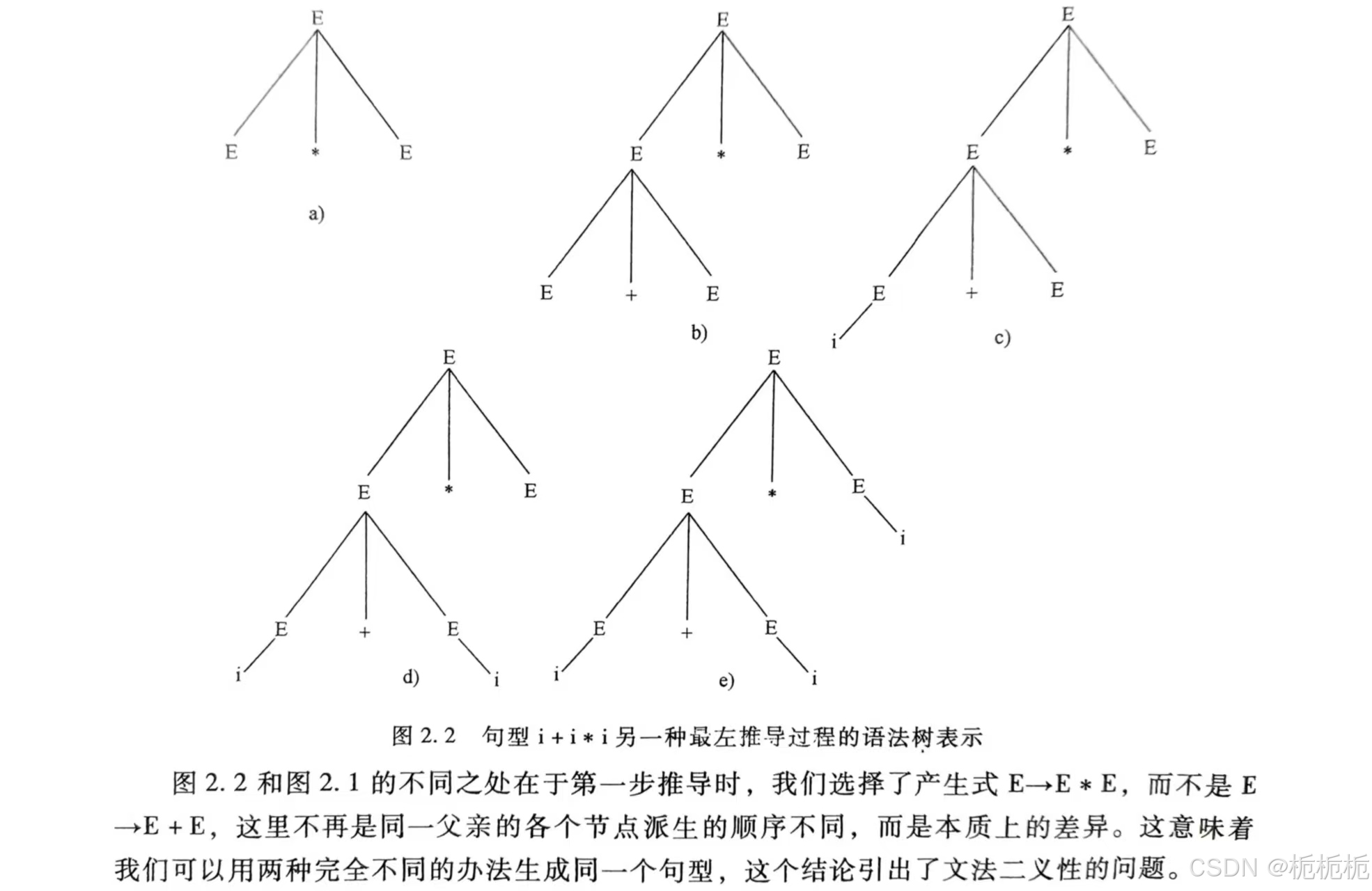
另一种不同的最左推导👇
总结:生成的树可能一样,也可能不一样。
文法二义性
对一个文法G,如果至少存在一个句子,有两棵(或两棵以上)不同的语法树,则称该句子是二义性的。包含有二义性句子的文法称为二义性文法。
若一个文法中存在某个句子,它有两个不同的最左(或最右)推导,则这个文法是二义性的。
??等价性定义:可以有两个文法和
,一个有二义性,另一个没有二义性,但却有
,即这两个文法是等价的,它们所产生的语言相同。
文法的二义性是不可判断的,即不存在一个算法,它能在有限步骤内,确切地判定一个文法是否是二义的。
文法等价变换
在LR类语法分析中,为了便于控制分析过程的结束,通常要求文法具有唯一的开始符并且开始符不出现于任何产生式的右部。如果不满足,需要对原文法进行等价变换,为此引入以下定理:
定理1
对任一文法都可以构造文法
,使得
,且
有这样的特点:文法的开始符唯一,并且不出现于任何产生式的右部。
证明:假设S是
的开始符,则只要在
中扩充一条新产生式
即可,其中Z是新的开始符。令这样扩充后的文法为
,它显然满足定理的要求。
定理2(消除空产生式)
对于任一文法(
),则可构造文法
,使得
,并且
中并无空产生式。

定理3(消除不可达产生式)
对任一文法都可以构造文法
,使得
,并且
的每个非终极符必出现在某个句型中。

定理4
对任一文法都可以构造文法
,使得
,并且
中没有特型产生式(左右都是非终结符)。

例:
设有如下文法:
P19 还有几道例题
有限自动机(FA)
有限自动机分为确定有限自动机(DFA)和非确定有限自动机(NFA)。
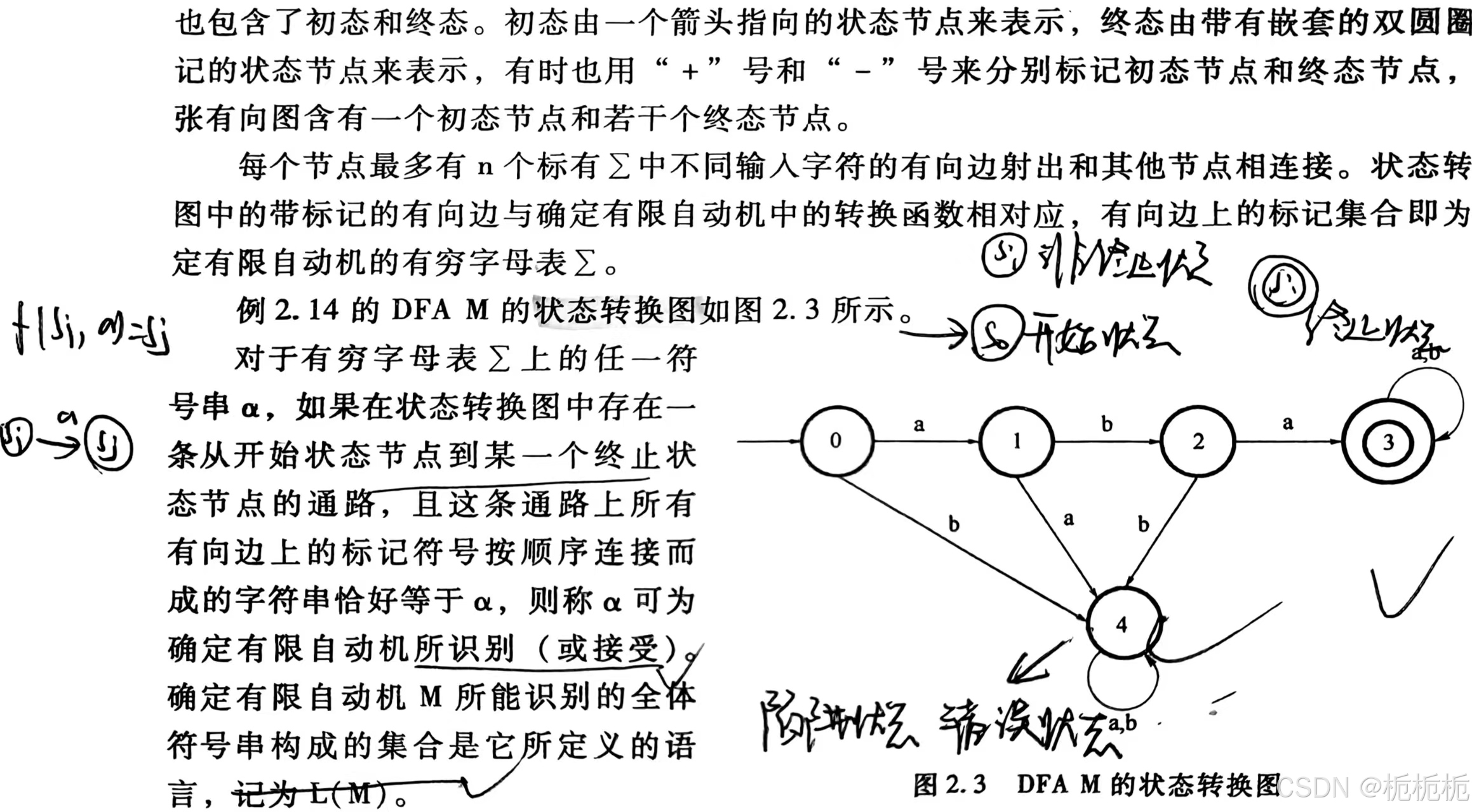
确定有限自动机


只有进入Z终止状态时,有限自动机识别/接受当前处理字符串,并不是进了这个状态就要终止了,终止状态也叫接受状态。
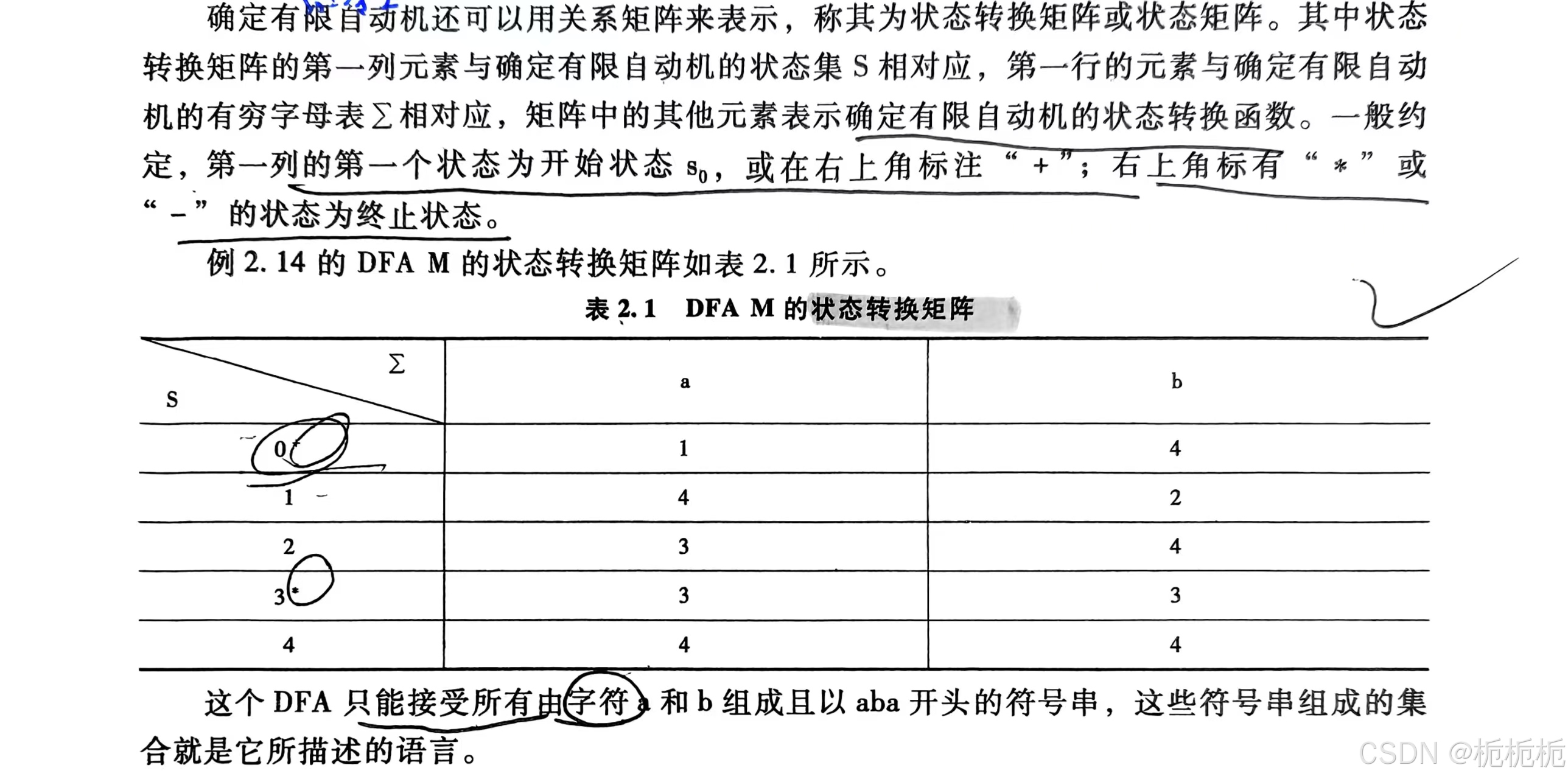
确定有限自动机还可以用关系矩阵来表示,也叫(状态)转换矩阵。
- 第一列元素与确定有限自动机的状态集S相对应;
- 第一行的元素与确定有限自动机的有穷字母表相对应;
- 矩阵中的其他元素表示确定有限自动机的状态转换函数。开始+,终止*或-;
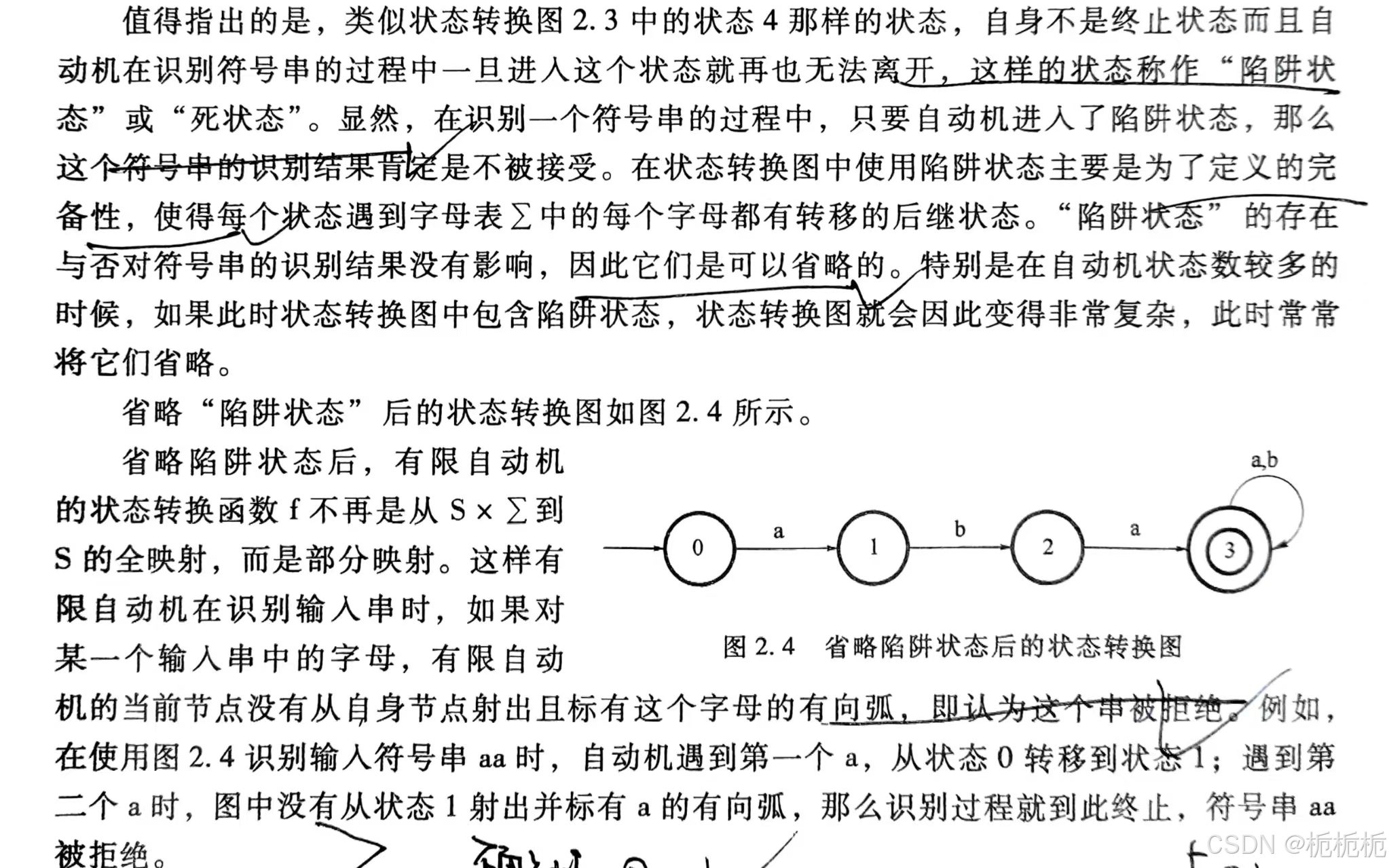
为什么只能是aba?因为别的就跑进“死胡同”了,又不能终止,又走不出来。
总结DFA:
确定有限自动机为啥确定?
- 初始状态唯一
- 映射是单值函数
- 没有输入为
的边,即不接受没有任何输入就转换的情况
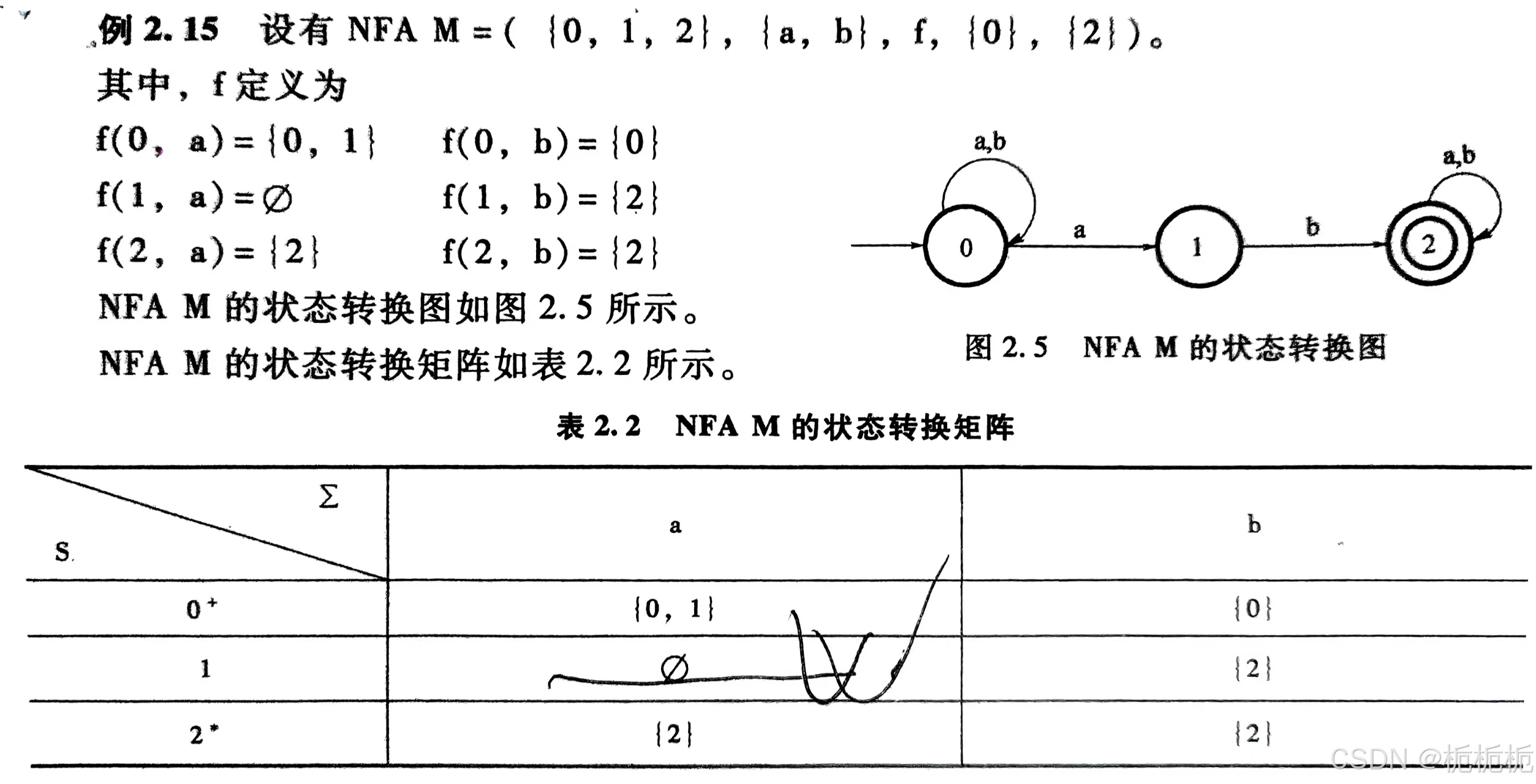
非确定有限自动机
接收一个字符允许跳转到多个后继状态。


例:
总结:
非确定有限自动机(NFA)
- 状态转换函数可为多值函数,一个状态接受同一个输入字符,可以转向多个不同后继状态。
- 允许有多个开始状态。
- 允许有空边,即在没有任何输入的情况下允许进行状态转换。
DFA与NFA的等价
对于给定的有限自动机和
,如果
,则称有限自动机
和
等价。
定理:对于任何一个NFA M,都存在一个DFA M',使得。


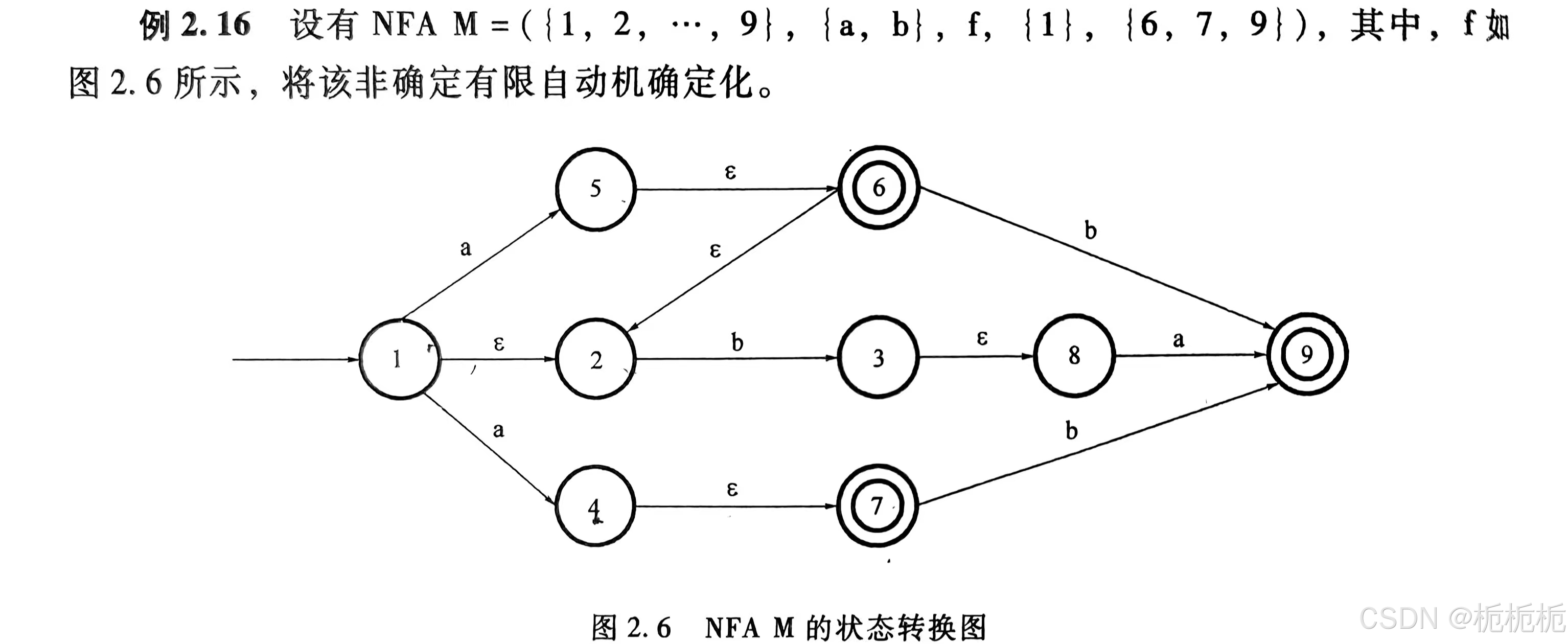
例:
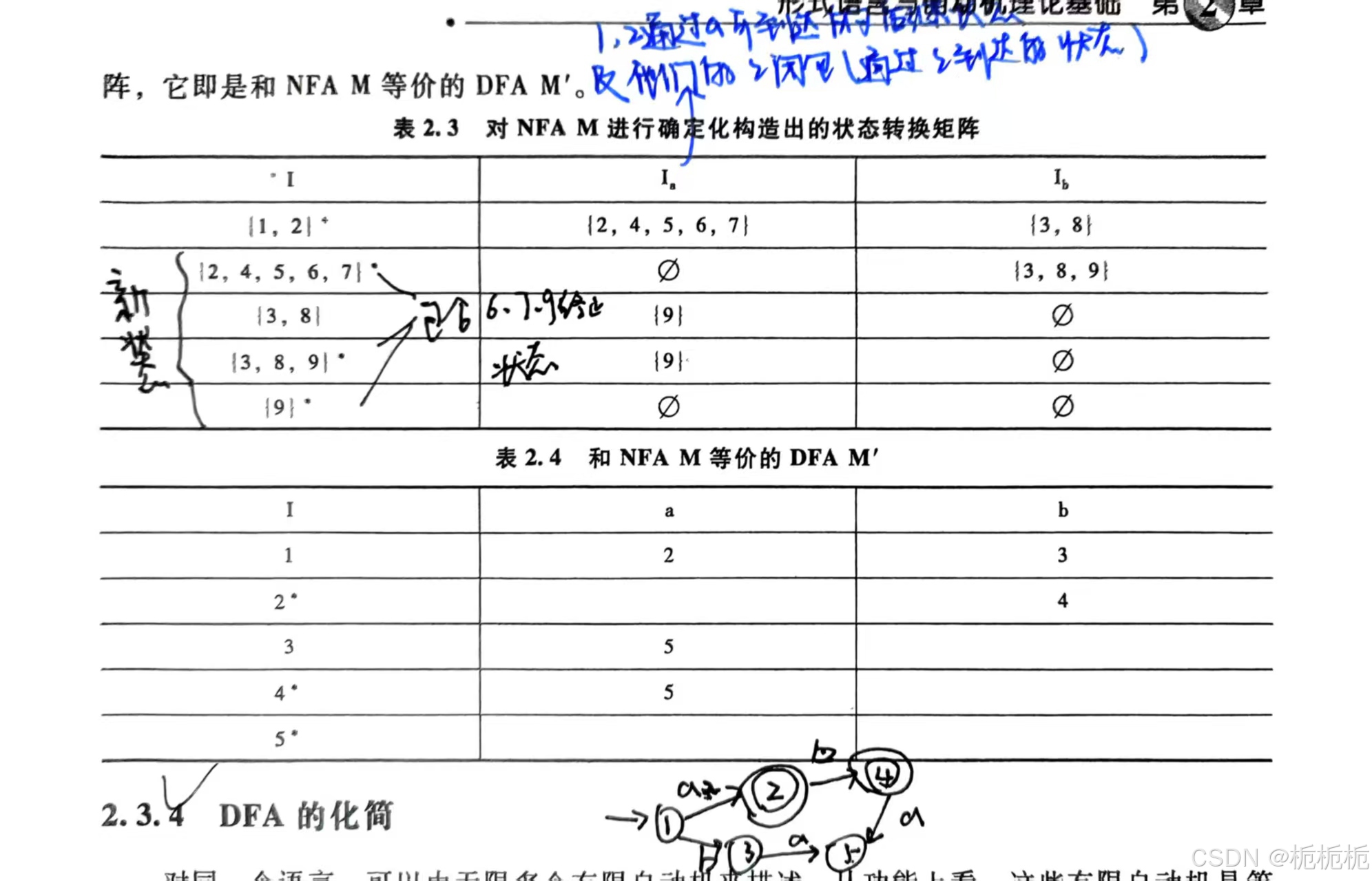
NFA(状态转换矩阵)和等价的DFA
PS:{2,4,5,6,7}怎么来的?{1,2}+经过a得到的{2,4,5}以及{2,4,5}的闭包(经过
){2,4,5,6,7},合起来就是{2,4,5,6,7}
DFA I列的1,2,3,4,5怎么来的?分别用1,2,3,4,5代表{1,2},{2,4,5,6,7},{3,8},{3,8,9},{9}这5个状态子集。(如下图红色部分)
正规式转化为NFA,NFA转化为DFA_哔哩哔哩_bilibili
DFA的化简
对一个NFA,把它等价变化为DFA后,得到的DFA所具有的状态数可能并不是最小的。那么,有没有一个最小的DFA呢?这就是有限自动机的最简或最小化问题。
一个确定有限自动机M的化简是指寻找一个状态数最少的DFA M',使得L(M)=L(M')
定义1:设DFA M的两个不同状态和
,如果对任意输入的符号串x,从
和
出发,总是同时到达接受或拒绝状态中,则称
和
是等价的。如果
和
不等价,则称
和
是可区分的。所接受的符号相同。
显然,DFA的终止状态和非终止状态是不等价的。
定义2:从有限自动机的初始状态开始,任何输入序列都不能到达的那些状态称为无关状态。
定义3:如果DFA M没有无关状态,也没有彼此等价的状态,则称DFA M是最小的(或规约的)。







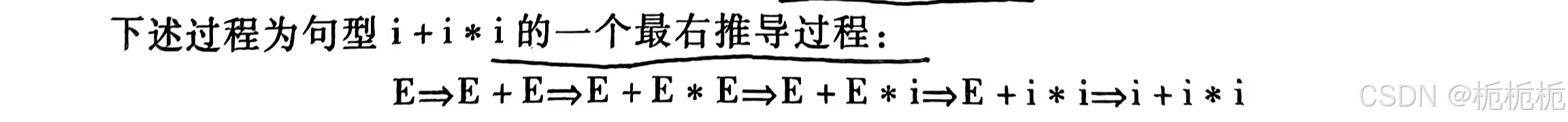
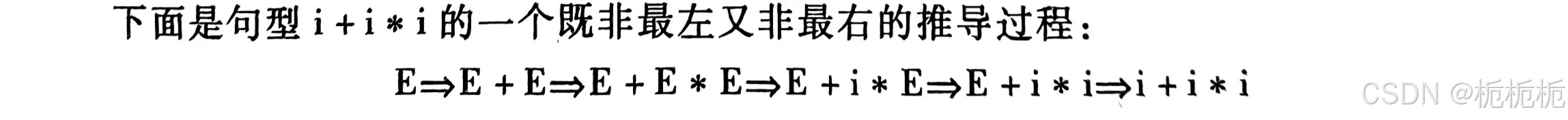
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








