TopCoder Tutorials:http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=binaryIndexedTrees#prob
1、要向上统计,向下修改;一般是修改一段区间的值,查找的是某个位上的值;
2、要向上修改,向下统计;一般是修改某个位置上的值,查找的是一段区间的和;
可以用树状数组的地方,一定可以用线段树;反过来则不然;
HDU1556 color the ball
http://acm.hdu.edu.cn/showproblem.php?pid=1556
基础题
区间修改,单点查询
HDU1166 敌兵布阵
http://acm.hdu.edu.cn/showproblem.php?pid=1166
基础题
单点修改,区间查询
hoj 2430 Counting the algorithms
http://acm.hit.edu.cn/hoj/problem/view?id=2430
这题其实是个贪心,从左往右或者从右往左,找与它相同的删去即可。先扫描一遍记录第一次出现和第二次出现的位置,然后我们从右到佐,每删去一对,只需要更改左边的位置的树状数组即可,因为右边的不会再用到了
HOJ 1867 经理的烦恼
http://acm.hit.edu.cn/hoj/problem/view?id=1867
经理的烦恼此题是最基本的一维树状数组题目,直接进行简单的加一减一(通过判素)操作即可。
HOJ2275 Number sequence
http://acm.hit.edu.cn/hoj/problem/view?id=2275
题目就是统计序列中Ai < Aj > Ak(i < j < k)的个数,可以从前往后统计每个元素之前小于它的数的个数,在从后往前统计每个元素之后小于它的数的个数。然后乘积加和即可。
poj2299 Ultra-QuickSort (求逆序数)
http://poj.org/problem?id=2299
用归并排序
求逆序数,也是树状数组的典型应用
求一堆数中前面比他大的数的个数;也需要向上统计,向下修改;
可以与求一串数中前面比他小的数的个数这个题来比较思考。
poj2352 stars
http://poj.org/problem?id=2352
相当经典的树状数组题目,第一感觉容易给人二维树状数组的印象。不过数据范围显然不容许的,先对第一维排序,然后再统计每个位置之前的星星的个数。
POJ3067 Japan与stars
http://poj.org/problem?id=3067
极其相似,唯一的不同是上题是统计之前的个数,而这个统计之后的个数;
当然我们可以用当前总数i减去之前的数即可得到。注意使用正确的数据类型。
poj2481 Cows
http://poj.org/problem?id=2481
这个题要把y按不降排序,x不升排序,基本是就是poj2352了。。不过注意其中可以有完全重合区间;
数轴上n个牛,their favourite clover range is [Si, Ei] and [Sj, Ej]. If Si <= Sj and Ej <= Ei and Ei – Si > Ej – Sj, we say that cowi is stronger than cowj.
统计出对于第i个牛,比他大的牛的个数。。。。
按照s排序,然后遍历(这时前面的x必然小于等于当前的x),然后统计E大于当前E的个数。。。边界情况特殊处理,
poj3321 apple Tree;
http://poj.org/problem?id=3321
这题要用到树状数组;但难度在那个dfs怎么求那个时间戳;求出后,在套入树状数组的那部分东东。就搞定了。。
题目大意为给出一棵树,节点数<=100000,树中的节点可能有苹果,两种操作:一种是改变某一节点的苹果,有改为无,无改为有。第二种操作是求某一节点和以该节点为根的子树的苹果总数。操作数达到了100000;
这题需要把一个树形结构变换为线性结构,然后使用树状数组动态求和。变换方法为DFS一次这棵树,记录下每个节点第一次访问和最后一次访问时的顺序编号,这时,在某节点第一次访问和最后一次访问编号之间的访问编号,必定为该节点的子节点,按照访问编号建立树状数组,当改变某一节点苹果时,只需按照该节点第一次访问的编号在树状数组中修改值,查询时统计某节点在第一次访问和最后一次访问编号之间的和。
这题的难点不在于树状数组,而是如果将整棵树映射到数组中。我们可以用DFS()改时间戳的方法,用begin[i]表示以i为根的子树遍历的第一个点,end[i]表示以i为根的子树遍历的最后一个点。
比如数据为:
5
1 2
2 5
2 4
1 3
那么begin[] = {1, 2, 5, 4, 3}, end[] = {5, 4, 5, 4, 3},下标从1开始。
对于每个点都对应一个区间(begin[i], end[i]),如果要改变点a的状态,只要Update(begin[a]),要求该子树的苹果树,即Getsum(begin[a] ) - Getsum(end[a] + 1),(注:这里求和是求x递增的路径的和。)
POJ2763 Housewife Wind
http://poj.org/problem?id=2763
也是树状数组+欧拉序列(和3321一样),并且用到了LCA(一开始认为不用,但确实得用),不过AC的好辛苦。。。。。。。确实是一道很好的题!!!!从上午11点一直wa到下午4点多。。。而且是因为一个bug。。。
这题就是给你一棵树,边上有权,然后维护两个操作,一个是问你从一个点走到另一个点的距离,另一个是改变一条边的权值。一开始想到很多 莫名其妙的算法,后来发现用dfs序列就很好。。。按照dfs序列构造一个树状数组,对于点i,begin[i]值为i到父节点的 权,end[i]=-begin[i],这样任意一个点到根节点的路径长就是getsum(begin[i])。这样i,j路径长度就是 getsum(begin[i])+getsum(begin[j])-2*getsum(begin[lca(i,j)]),求lca方法有rmq和 tarjan,因为我半秃只会用tarjan,所以写的非常麻烦(要离线做,开n个数组)。。。这同时导致了杯具的发生。tarjan中一个<=号 我打成了<,这样如果求i和i的lca,返回0.。。。。。。
另外,这题递归层数好像挺深。。。vc的栈还真挺大。还有就是只要能在线做的尽量在线做。。。离线要开的数组太多了。。。脑子都晕了
POJ3378 Crazy Thairs
http://poj.org/problem?id=3378
在一个序列中统计:
1. 1 ≤ i < j < k < l < m ≤ N
2. Ai < Aj < Ak < Al < Am
的个数。。
有点像hoj2275,以中间元素为轴,分别统计两边,但由于两边各有两个,因此需要用两个树状数组来统计。。。。
注意最后要用到高精度。。。囧。。
POJ2182 Lost Cows
http://poj.org/problem?id=2182
1…N个数的某种序列,第i个数为arr[i],前面比他小的数的个数为val[i]。已知val序列,求arr序列。。。。
从后向前遍历,用树状数组统计,中间加入二分查找。。。效率n*lgn*lgn。
POJ3416 Crossing
http://poj.org/problem?id=3416
star的升级版。。。。两个树状数组就可以搞定了。。。
先提个注意点,由于Lowbit(0) = 0,这会导致x递增的那条路径发生死循环,所有当树状数组中可能出现0时,我们都全部加一,这样可以避免0带来的麻烦~~
Sgu 180 Inversions
http://acm.sgu.ru/problem.php?contest=0&problem=180
经典树状数组 + 离散化。注意结果要用long long~~ //求逆序对
UVA 11610 Reverse Prime
一道很综合的树状数组题,用到了树状数组中的很多知识点,包括离散化,二分查找等。
1. 先按题目要求筛法素数,找到所有的Reverse Prime。
2. 将这些Reverse Prime离散化,只有78500个左右。树状数组中tree[i]记录比i小的点的个数。
当执行q a操作时,二分查找最小的j, 使得Getsum(j) 等于 ++a(因为a可能为0,所以统一加一)。这步与上面SPOJ 227 Ordering the Soldiers 类似。
3. 当执行d a操作时,先找到a离散化后的值b,然后Update(b, -1)即可。
按这样做后,运行时间为: 0.3s多,感觉很诧异,因为都是0.1s以下的。这里特别感谢liuzhe大牛的指点,其实题目中的Reverse Prime是由10^6以下的素数倒置得到的,那么得到的要求是7位,最后一位一定是0,我们可以对每个除以10处理,那么数的范围就减小了10倍,速度就提高了不少。
poj1990 MooFest
http://poj.org/problem?id=1990
这题O(n^2)算法必然超时;排序后要存储前面比他小的数的总和,和个数;故树状数组;
很经典的一道题,数轴上有n个牛,每个牛在一个坐标x[i]上,并且有一个值v[i],要求计算所有的1<=i<j<=n的abs(x[j]-x[i]) * max(v[i], v[j])的值。。
先按照v进行升序排序,然后遍历,用两个树状数组统计出小于(大于)x[i]的牛个数and小于(大于)x[i]的牛的x之和,这样可以快速统计出来。。。
Hdu 3015 Disharmony Trees
跟上题方法相同,只要按它的要求离散化后,按高度降序排序,套用上题二个树状数组的方法即可。
TJU3243 Blocked Road
这题主要在于如果判断是否连通,我们可以先用j = Getsum(b) –Getsum(a –1),如果j等于(b –a)或者Getsum(n) –j等于(n –(b –a)),那么点a, b联通。
SPOJ 227 Ordering the Soldiers
这题与正常的树状数组题目正好想反,给定数组b[i]表示i前面比a[i]小的点的个数,求a[]数组。我们可以先想想朴素的做法,比如b[] = {0, 1, 2, 0, 1},我们用数组c[i]表示还存在的小于等于i的个数,一开始c[] = {1, 2, 3, 4, 5},下标从1开始。我们从右向左扫描b[]数组,b[5] = 1,说明该点的数是剩下的数中第4大的,也就是小于等于它的有4个,即我们要找最小的j符合c[j] = 4(这里可以想想为什么是最小的,不是最大的,挺好理解的),而c[]是有序的,所以可以用二分来找j,复杂度为O(logn),但现在问题是每次更新c[]要O(n)的复杂度,这里我们就想到树状数组,c[i]表示还存在的小于等于i的个数,易见树状数组处理方法。处理每个位置的复杂度为O(logn * logn),总的复杂度为O(n * logn * logn)。
HDU2852 KiKi's K-Number
这题与上面那题类似,只是要求比a大的第k大的数,那我们用Getsum(a)求出小于等于a的个数,那么就是要我们求第k + Getsum(a)大的数,而删除操作只要判断Getsum(a) –Getsum(a -1)是否为0,为0则说明a不存在。
给力题
NOI 2008 糖果雨
CDQ教母为NOI出的经典树状数组题目,有兴趣的同学自行了解,就不提供相关资料了。
二维树状数组
poj2155 Matrix
http://poj.org/problem?id=2155
二维树状数组。注意一个转化,即把更新与求和对应的down,up互换.即考虑一维时,比如需要更新[a,b],我们只要更新b的down集合+1,以及a-1的down集合-1就可以,这样就可以保证只更新了[a,b],因为他们中的节点的父亲集合里只有一个会被更新。而查询时只需要计算所有父亲的和就可以得到被修改的次数了。然后一维的情况便可以推广到二维情况里,即[x1,y1][x2,y2]组成的矩形,一次置0可以分解成对四个以原点[1,1]为左上点的矩形的运算和。即把一个矩形的操作,转化成4个矩形的操作。
此题是二维树状数组基本应用的变通,不像hoj1640简单的插入统计,而此题是对一个二维区间数值翻转(0变1,1变0),最后询问某处的值。所以可以使用奇偶性判断,这样我们可以使用树状数组在这个二维区间内加,就相当于翻转,最后统计某点翻转的次数。
楼教主出的题目~~原题是二维的,我们先化简为一维的讨论。
题目要求有两种操作 :
1. 改变某个(a, b)内的所有。
2. 求某个点(a)的值。
以下是个人的理解:
很明显,这题与树状数组的操作正好相反。我们可以想想树状数组中的两个函数Update()修改某个点的值(准确说是某个路径,递增或递减),Getsum()求和区间(1, x)内的点的值。我们上面已经分析了,这两个函数本质上是相同的,可以互相调换的。换句话说就是修改某点x和求和某个区间(1, x)是可以互相调换的,即我们可以用Getsum(x, c)修改(1, x)这个区间内的点的值,而用Update(x)来求该点的值。而两个函数的写法与原来完全相同(或者说就函数名调换了下),仅仅是思想变化了下。(这里很难理解就是因为只是思想变化,而程序与原来基本没变)
那么回到原题,我们要使区间(a, b)内的点 + c,只需要使区间(1, b)内的点+c,而区间(1, a-1)内的点-c即可。如果是二维的,修改矩阵(x1, y1)到(x2, y2),即(x2, y2)+c, (x1-1,y2)-c, (x2, y1-1)-c, (x1-1,y1-1)+c即可。
总结:通过以上的分析,我们可以发现其实Update()和Getsum()这两个函数是相同的,我们可以用Up()和Down()来代替它们。Up()为操作x递增的路径,Down()为操作x递减的路径。
Up()和Down() 有四种组合 :
1. Up()表示修改单点的值,Down()表示求区间和。
2. Down()表示修改单点的值,Up()表示求区间和。
3. Up()表示修改区间,Down()表示求单点的值。
4. Down()表示修改区间,Up()表示求单点的值。
1和2根据求比它大还是比它小来选择,而3和4种适用条件则相同,用其中一种即可。
两道赤裸裸的二维树形数组
hdu1892 See you~
http://acm.hdu.edu.cn/showproblem.php?pid=1892
hdu2842 Stars
http://acm.hdu.edu.cn/showproblem.php?pid=2642
稍微变化一点
hdu2227 Find the nondecreasing subsequences
http://acm.hdu.edu.cn/showproblem.php?pid=2227
Hdu2688 Rotate
http://acm.hdu.edu.cn/showproblem.php?pid=2688
POJ1656 Counting Black
http://poj.org/problem?id=1656
水题,直接朴素就可以,二维树状数组可以加一些优化。。。不过是插段问段的,所以必然有一个(插入或者是查询)需要n^2效率
poj1195 Mobile phone
http://poj.org/problem?id=1195
是个二维的情况。改变的是某个位置上的数的大小;就将所有管辖这个点的 点修改;
统计的时候,就是向下统计;
SPOJ 1029 Matrix Summation
https://www.spoj.pl/problems/MATSUM/
基本的二维树状数组...
POJ 2029 Get Many Persimmon Trees
http://poj.org/problem?id=2029
O(n ^ 2)枚举起点,再用二维树状数组求其中的点数即可。
HOJ 2686 Magic-Box
http://acm.hit.edu.cn/hoj/problem/view?id=2686
三维树状数组,裸到极致。
难题:
POJ 2464 Brownie Points II
http://poj.org/problem?id=2464
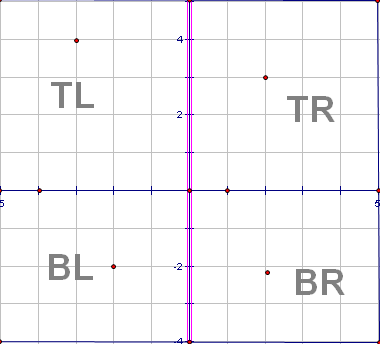
这道题用二分也可以做的,这里介绍下树状数组的做法。首先有n个点,过每个点可以做x,y轴,把平面切成BL, TL, TR, BR四个部分,我们现在的问题是如果快速的计算这四个部分的点的个数。
这样我们可以先预处理,先按y坐标排序,求出每个点正左方和正右方的点的个数LeftPoint[], RightPoint[],复杂度为O(n),同样我们再以x坐标排序,求出每个点正上方和正下方点的个数UpPoint[], DownPoint[]。还要求出比点i y坐标大的点的个数 LageY[]。注意:这里要进行下标映射,因为两次排序点的下标是不相同的。
然后按x坐标从小到大排序,x坐标相等则y坐标从小到大排序。我们可以把y坐标放在一个树状数组中。
对于第i个点,求出Getsum(y[i])即为BL的个数,然后Update(y[i])。由于现在是第i点,说明前面有i – 1个点, 那么
TL = i - 1 - LeftPoint[i]- BL;
TR = LargeY[i] - TL – UpPoint[i] ;
BR = n - BL - TL - TR - LeftPoint[i] - RightPont[i] - UpPoint[i] – DownPont[i] - 1;
这样我们就求出四个部分的点的个数,然后判断有没有当前解优,有的话就更新即可~~

























 412
412

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








