[翻译]CoolStreaming/DONet: 实时流媒体传输的数据重叠网络 (2)

[翻译]CoolStreaming/DONet: 实时流媒体传输的数据重叠网络 (2)

CoolStreaming/DONet: 实时流媒体传输的数据重叠网络

作者: Xinyan Zhang, Jiangchuan Liu, Bo Li, Tak-Shing Peter Yum
翻译: 默难 ( monnand@gmail.com ). DriftingLeaves ( driftingleaves@yahoo.com )
原文参见: http://citeseer.ist.psu.edu/zhang05coolstreamingdonet.html
本文其他部分参见: http://blog.csdn.net/monnand/category/261378.aspx

IV. 网络半径的分析   ( 本节翻译: 默难 )

本节将会对 DONet 网络的半径进行分析. 所谓网络半径, 指的是一个分段在传递过程中, 从源结点到所有的目的结点的平均距离. 和大多数文献 [11] , [12], [27] 相同, 距离的单位是经过网络中结点的跳数. 这在一定程度上反应了端到端的传输延迟. 这里用到的分析模型是经过简化的, 结果显示网络半径与网络大小之间成对数关系. 这说明 , DONet 网络中的端到端延迟是较小的, 足以用来传输实时的流媒体.

在 DONet 网络中, 分段可用性信息的传递路径, 可以用一棵广度优先搜索 ( BFS, Breadth-First Search) 的树结构来表示. 源结点是树的根结点, 处于第 0 层. 第 k 层的结点与源结点之间相隔 k 跳. DONet 的结点不会维护一个明确的结构, 因此, 每个结点可以在这个 BFS 树中出现多次.

为了描述方便, 把 BFS 树中的结点称为 s-结点 ( s-node ). 根据广度优先搜索的规则, s-结点按照在搜索时被访问的顺序进行编号. 这样, 根结点的编号为 1. 对于编号为 t 的 s-结点, 它所对应的 DONet 结点被表示为 pt ( 译者注: 根据下面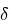(t) 函数的定义, 此处应为 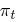). 假设伙伴之间的带宽大约相等, 并且一个分段到达一个结点的过程, 是自根结点出发, 按照广度优先的算法搜索树结构, 直到该结点第一次出现. Fig-4 显示了 Fig-2 的 DONet 网络的 BFS 树结构 ( 只列举了三个层次).

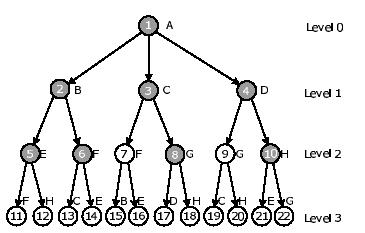
Fig-4 一棵广度优先搜索的数. 黑色的结点表示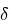(t)等于1的结点. 即第一次出现的结点. 白色结点表示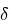(t)等于零的结点.

定义一个辅助函数 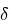(t):

 

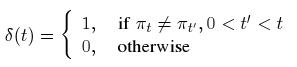
也就是说, 只有在 s-结点 t 第一次在树结构中出现时, 函数值才为 1. 由于成员关系和伙伴关系协议是采用随机的伙伴选择方式, 用 N 表示网络中的结点数量, 因此则有:

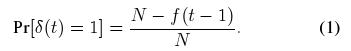
这里, f(t) 表示编号为 1 至 t 的 s-结点中, 包含的 DONet 结点的数量. 由此则有: f(t) - f(t-1) = 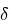(t). 对 (1) 式两遍同时求期望, 则有:

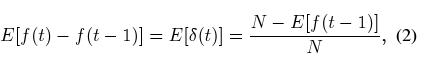
由此推导出:

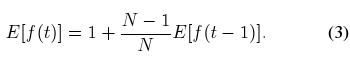
因为 f(1) = 1, 根据等式 (3) 可以推导出:

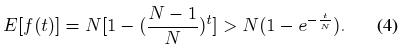
这一关系给出了 DONet 结点数目关于 s-结点编号的函数. 令t_k表示第 k 层中最后一个 s-结点的编号, 那么 DONet 网络中其他结点与源结点之间的平均距离, 即网络半径, 则为:

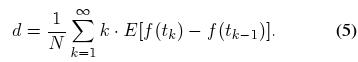
注意到, 当 k 趋近于无穷时, 有: 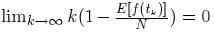. 对于一个连通的网络来说, 可得:

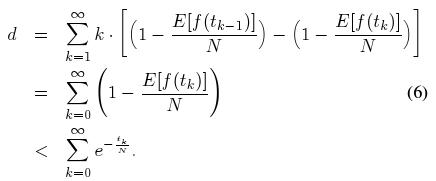
考虑一种稳定的状态: 每个 DONet 结点均拥有 M 个伙伴. 那么对应的 BFS 树中, 除了根结点拥有 M 棵子树外, 每个非叶子结点都拥有 M-1 棵子树. 那么可以导出:

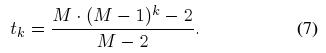
将 (6) 式中的连加分解为两部分: 一部分是从 k = 0 到 k = log_M-1N; 另一部分是从 k = 1 + log _M-1N 到正无穷. 那么有: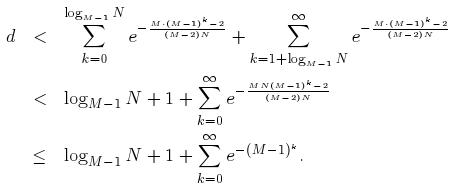

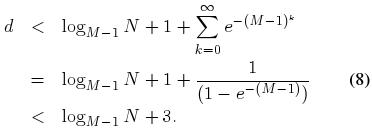
当 M 大于等于 3 时, 有 (M-1)^k >= (M-1)k. 则 e^{M-1^k} <= e^-(M-1)k. 由此导出:

由此, 源结点到网络中任意结点的平均距离则为 O(logN). 从式 (4) 和式 (8) 可以看出, 从源结点出发, 在 k 跳之内可以到达的结点的比例为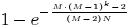. 也就是说, 对于包含 500 个结点的 DONet 网络, 设 M = 4, 那么, 大约 95% 的结点可以在 6 跳之内到达.