三角形数

最新推荐文章于 2021-12-22 20:05:48 发布

MIsike

最新推荐文章于 2021-12-22 20:05:48 发布

阅读量3k

点赞数

分类专栏：数学

9 篇文章 0 订阅

订阅专栏

三角形数[编辑]

维基百科，自由的百科全书

本条目需要扩充。（2013年2月14日）
请协助改善这篇条目，更进一步的信息可能会在讨论页或扩充请求中找到。请在扩充条目后将此模板移除。

一定数目的点或圆在等距离的排列下可以形成一个等边三角形，这样的数被称为三角形数。比如10个点可以组成一个等边三角形，因此10是一个三角形数：

一开始的18个三角形数是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153、171……（OEIS中的数列A000217）

三角形数

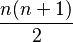第n个三角形数的公式是 $\frac {n (n+1)}{2}$ 。
第n个三角形数是开始的n个自然数的和。
所有大于3的三角形数都不是质数。
开始的n个立方数的和是第n个三角形数的平方（举例：1 + 8 + 27 + 64 = 100 = 10²）
所有三角形数的倒数之和是2。
任何三角形数乘以8再加1是一个平方数。
一部分三角形数（3、10、21、36、55、78……）可以用以下这个公式来表示： $n*(2n+1)$ ；而剩下的另一部分（1、6、15、28、45、66……）则可以用 $n*(2n-1)$ 来表示。
一种检验正整数x是否三角形数的方法，是计算：

$n = \frac{\sqrt{8x+1}-1}{2}.$

如果n是整数，那么x就是第n个三角形数。如果n不是整数，那么x不是三角形数。这个检验法是基于恒等式 $8T_n + 1 = S_{2n + 1}.$

55、5,050、500,500、50,005,000……都是三角形数。
第11个三角形数（66）、第1111个三角形数（617,716）、第111,111个三角形数（6,172,882,716）、第11,111,111个三角形数（61,728,399,382,716）都是回文式的三角形数，但第111个、第11,111个和第1,111,111个三角形数不是。