GBDT算法笔记

最新推荐文章于 2023-06-24 18:41:36 发布

五四三两幺-发射!

最新推荐文章于 2023-06-24 18:41:36 发布

阅读量506

点赞数

分类专栏：人工智能机器学习文章标签： GBDT 机器学习 boosting 提升树

本文链接：https://blog.csdn.net/ying86615791/article/details/103261360

版权

人工智能同时被 2 个专栏收录

14 篇文章 0 订阅

订阅专栏

机器学习

5 篇文章 0 订阅

订阅专栏

概述：
GBDT算法可以看成是由M棵树CART回归树组成的加法模型，
该模型使用前向分布算法来学习，
在前向分布算法中，每一步只学习一个基函数(基模型)及其系数，逐步逼近优化目标函数
在回归问题中，当采用平方误差损失时，那么GBDT每一步目标是去拟合到上一步为止学到的模型与真实样本的残差

GBDT来自提升树，下面从5个方面来学习GBDT算法
1.CART回归树
2.加法模型与前向分布算法
3.回归问题的提升树
4.GBDT算法
5.GBDT用于二分类问题

1.CART回归树

(内容来自《统计学习方法》)
▲回归树是二叉树
▲选择切分点时，要计算所有变量的每一个取值(样本集合中在该变量上的所有出现的值)作为切分点的loss；假如有m个变量，每个变量有am个取值，那么要计算m*am次loss，选择loss最小的 变量及其取值 作为切分点，将样本空间分成两份(上图中的R1和R2)
▲回归树的叶子节点的输出值=该区域所有样本标签值的平均
▲回归树最后会将输入样本划分到1个确定的叶子节点上，该输入样本的输出值=该叶子节点的输出值

2.加法模型与前向分布算法

(内容来自《统计学习方法》)
▲Adaboost是前向分布加法算法的特例，这时，模型是由基本分类器组成的加法模型，损失函数是指数函数。参考《统计学习方法》P145-定理8.3

3.回归问题的提升树

(内容来自《统计学习方法》)
▲提升树是GBDT的前身，是加法模型，基函数是CART回归树
▲回归问题中，提升树把每一步学到的输出叠加起来作为最终的输出
▲回归问题中，如果使用平方误差损失，那么每一步是拟合数据的残差

4.GBDT算法

(内容来自《统计学习方法》)
▲主要思想：算法利用损失函数的负梯度在当前模型的值，作为回归问题提升树算法中的残差的近似值。(当损失函数使用均方差时候，相当于是残差，跟回归问题的提升树一样)
▲第(1)步目的是找到1个常数c使损失最小，作为模型的初始输出。如果损失是凸函数，可以求导，令导数=0，得到c。对于平方误差损失，求导后的出来c就是所有样本标签的均值
▲第(2b)步根据负梯度的值(如果是平方差损失, 这个值就是样本的残差)，拟合1个回归树，用来估计节点区域划分。
▲第(2c)步在第(2b)步估计好的节点区域上，分别估计每个区域的输出值(有一个常数c,与第(1)步的c不一样)。如果损失是凸函数，可以求导，令导数=0；对于平方误差损失，与第(1)步一样，求导后的出来c=该区域所有样本标签(此时标签为残差)的均值，这样的话，就是普通回归树的叶节点区域输出值估计方法，在第(2b)步就可以确定了。
▲GBDT使用的决策树是CART回归树，无论是处理回归问题还是二分类以及多分类，GBDT使用的决策树通通都是都是CART回归树。为什么不用CART分类树呢？因为GBDT每次迭代要拟合的是梯度值，是连续值所以要用回归树
▲GBDT做分类？还是一样的加法模型，只需要往加入激活函数即可

以上是GBDT算法的一般流程(回归和分类通用), 有关GBDT回归的更多原理与例子参考这里。

5.GBDT用于二分类问题

还是用加法模型，还是用CART回归树，只需要在模型的输出上加入1个sigmoid激活函数.
算法最终的模型为:
$f(x)=P(F_{M}(x))=\frac{1}{1+e^{-F_{M}(x)}}, f(x)\in(0,1)$ ,
其中， $\dpi{100} F_{M}(x)$ 是加法模型中多个回归树的叠加值:
$F_{M}(x)=\sum _{m=0}^{M}h_{m}(x)$ ,
$P(Z)$ 是sigmoid函数，导数为:
公式(1) $P'(Z)=P(Z)[1-P(Z)]$ .

GBDT用于二分类问题时的求解算法还是和回归问题中的一样, 在求出负梯度后, 还是用负梯度去拟合回归树, 只不过
1.损失函数由MSE变为sigmoid的损失(即binary cross entropy, BCE)
2.相应的,模型的初始值的求解方法也变了
3.相应的,损失函数的负梯度在当前模型的值也变了(回归问题中可推导出= $y_{i}-F_{m-1}(x_{i})$ ,即样本的biao'q样本的残差)
4.相应的叶节点区域的估计方法也变了

假设到前m-1步为止学到的加法模型的叠加值为:
$F_{m-1}(x)=\sum _{k=0}^{m-1}h_{k}(x)=Z$ ,
那么在第m步的学习中,令样本在当前模型的值为
$z_{i}=F_{m-1}(x_{i})$
下面分别讲:

A.单个样本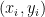 $(x_{i},y_{i})$ 的损失(BCE损失)

单个样本的损失(BCE损失)为:
$L(y_{i},\hat{y_{i}})=-y_{i}log\hat{y_{i}}-(1-y_{i})log(1-\hat{y_{i}})$ ,
其中 $\hat{y_{i}}$ 是用前m-1步的加法模型对样本做出的预测:
公式(2) $\hat{y_{i}}=P(z_{i})=\frac{1}{1+e^{-z_{i}}}$ ,

B.在第m步样本的损失的负梯度

那么在第m步该样本的损失的负梯度在当前模型的值为：
$r_{mi}=-\frac{\partial L(y_{i},\hat{y_{i}})}{\partial z_{i}}=\frac{y_{i}}{\hat{y_{i}}}\cdot \frac{\partial \hat{y_{i}}}{\partial z_{i}}+\frac{(1-y_{i})}{(1-\hat{y_{i}})}\cdot (-1)\cdot \frac{\partial \hat{y_{i}}}{\partial z_{i}}$
由公式(1)和公式(2)可得:
$\frac{\partial \hat{y_{i}}}{\partial z_{i}}=\hat{y_{i}}(1-\hat{y_{i}})$ ,
那么负梯度的值就为:
公式(3) $r_{mi}=-\frac{\partial L(y_{i},\hat{y_{i}})}{\partial z_{i}}=\frac{y_{i}}{\hat{y_{i}}}\cdot \hat{y_{i}}(1-\hat{y_{i}})+\frac{(1-y_{i})}{(1-\hat{y_{i}})}\cdot (-1)\cdot \hat{y_{i}}(1-\hat{y_{i}}) \\=y_{i}(1-\hat{y_{i}})+\hat{y_{i}}(y_{i}-1) \\=y_{i}-\hat{y_{i}} \\=y_{i}-\frac{1}{1+e^{-z_{i}}}$ ,

算出所有样本的 $r_{mi}, i=1,2,...n$ 后, 用 $r_{mi}$ 去拟合1个回归树, 就可以得到J个节点区域划分 $R_{mj}, i=1,2,...J$ .

从公式(3)的推导可以继续得出
$-r_{mi}=\frac{\partial L(y_{i},\hat{y_{i}})}{\partial z_{i}}=\frac{\partial L(y_{i},P(z_{i}))}{\partial z_{i}}=P(z_{i})-y_{i}$
即:
公式(4) $\frac{\partial L(y_{i},P(Z)))}{\partial Z}=P(Z)-y_{i}$

C.算法的第一步中, 模型的初始值

回到算法的第一步, 需要为模型求1个初始值满足
$F_{0}(x)=c_{0}=\mathop{\arg\min}_{c_{0}}\sum_{i=0}^{n} L(y_{i},P(c_{0})))$ ,
要求解上式, 那么根据公式(4), 令
$\frac{\partial \sum_{i=0}^{n} L(y_{i},P(c_{0})))}{\partial c_{0}}= \sum_{i=0}^{n}[P(c_{0})-y_{i}]= \sum_{i=0}^{n}[\frac{1}{1+e^{-c_{0}}}-y_{i}]=0$
可得
$\frac{1}{1+e^{-c_{0}}}=\frac{1}{n}\sum _{i=0}^{n}y_{i} \\ \Rightarrow c_{0}=log\frac{\sum_{i=0}^{n} y_{i}}{\sum_{i=0}^{n} (1-y_{i})}$

D.每个节点区域的输出值的估计

然后是估计每个节点区域的输出值(最难的一步?)
要求每个区域输出值, 需满足:
公式(5) $c_{mj}=\mathop{\arg\min}_{c}\sum_{x_{i}\in R_{mj}} L(y_{i},P(z_{i}+c))$
注意, $P(z_{i}+c)=\frac{1}{1+e^{-F_{m-1}(x)+c}}=\hat{y'_{m}}$ ,是在本次步骤(目前正在学习的第m步)对样本 $x_{i}$ 做出的预测. (前面的 $\hat{y_{i}}$ 是在上一步, 也就是第m-1步做出的预测)
令
$Loss(Z+c)=\sum_{x_{i}\in R_{mj}} L(y_{i},P(z_{i}+c))$
$Loss(Z)=\sum_{x_{i}\in R_{mj}} L(y_{i},P(z_{i}))$
把公式(4)带入上式可得(c是常数, 复合函数中的导数为1)
公式(6) $Loss'(Z+c)=\frac{\partial Loss(Z+c)}{\partial c}=\sum_{x_{i}\in R_{mj}} [P(z_{i}+c)-y_{i}]$ ,
要求出最优的c, 需要令公式(6)=0, 再求出c, 然而这样很难求

继续, 换一种思路, 用泰勒公式去逼近这个值
首先把公式(6)与公式(1)联立，求2次导可得
公式(7) $Loss''(Z+c)=\frac{\partial Loss'(Z+c)}{\partial c}\\ =\sum_{x_{i}\in R_{mj}} [P(z_{i}+c)(1-P(z_{i}+c))]$
其次, 引入泰勒公式的一阶展开式
公式(8) $f(x+a)=f(x)+f'(x)\cdot a$
则
公式(9) $Loss'(Z+c)=Loss'(Z)+Loss''(Z)\cdot c$
令上式=0, 并带入公式(6)和公式(7)得
$c=-\frac{Loss'(Z)}{Loss''(Z)}=\frac{\sum_{x_{i}\in R_{mj}} [y_{i}-P(z_{i}+c)]}{\sum_{x_{i}\in R_{mj}} [P(z_{i}+c)(1-P(z_{i}+c))]}$
$c_{mj}=c$ 即为区域Rmj的最优输出值

最后
更新加法模型:
$F_{m}(x)=F_{m-1}(x)+\sum_{j=1}^{J}c_{mj}I(x\in R_{mj})$
激活函数输出:
$\hat{y'_{m}}=P(F_{m}(x))=\frac{1}{1+e^{-F_{m}(x)}}$

本文参考这里和这里.
sklearn中的GBDT调参
未来: GBDT用于多分类问题?

五四三两幺-发射!

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
GBDT算法笔记

目录1.CART回归树2.加法模型与前向分布算法3.回归问题的提升树4.GBDT算法5.GBDT用于二分类问题A.单个样本的损失(BCE损失)B.在第m步样本的损失的负梯度C.算法的第一步中, 模型的初始值D.每个节点区域的输出值的估计概述：GBDT算法可以看成是由M棵树CART回归树组成的加法模型，该模型使用前向分布算法来学习，在前向分布算法中，每一...
复制链接

扫一扫