矩阵的逆怎么算？逆矩阵公式来了(附逆矩阵计算器)

大家好，这里是效率办公指南！

📚 在线性代数中，逆矩阵是一个非常重要的概念。一个方阵如果存在逆矩阵，意味着该矩阵是可逆的，或者说是非奇异的。逆矩阵在解决线性方程组、计算矩阵的方根等方面有着广泛的应用。今天，我们将介绍如何求矩阵的逆，提供逆矩阵的计算公式，并展示具体的计算示例。

逆矩阵的计算公式

对于一个可逆的方阵 A ，其逆矩阵 A^-1满足以下条件：

其中 I 是单位矩阵。求逆矩阵通常可以通过以下几种方法：

1. 高斯-约当消元法

这是最常用的方法，通过行变换将矩阵 A 转换为单位矩阵，同时对单位矩阵进行相同的行变换，最终单位矩阵变为 A^-1。

2. 伴随矩阵法

对于一个 n×n 的矩阵 A，其逆矩阵可以通过以下公式计算：

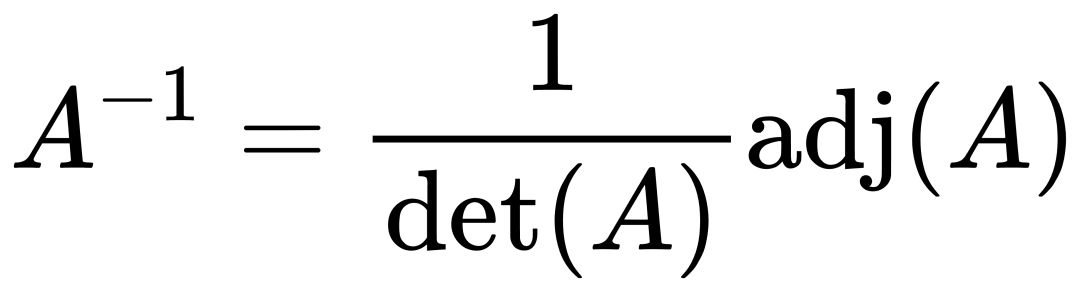
其中  det(A)  是矩阵  A  的行列式， adj(A)  是  A  的伴随矩阵，伴随矩阵由  A  的各个元素的代数余子式组成。

逆矩阵计算示例

示例 1：2x2 矩阵

考虑矩阵：

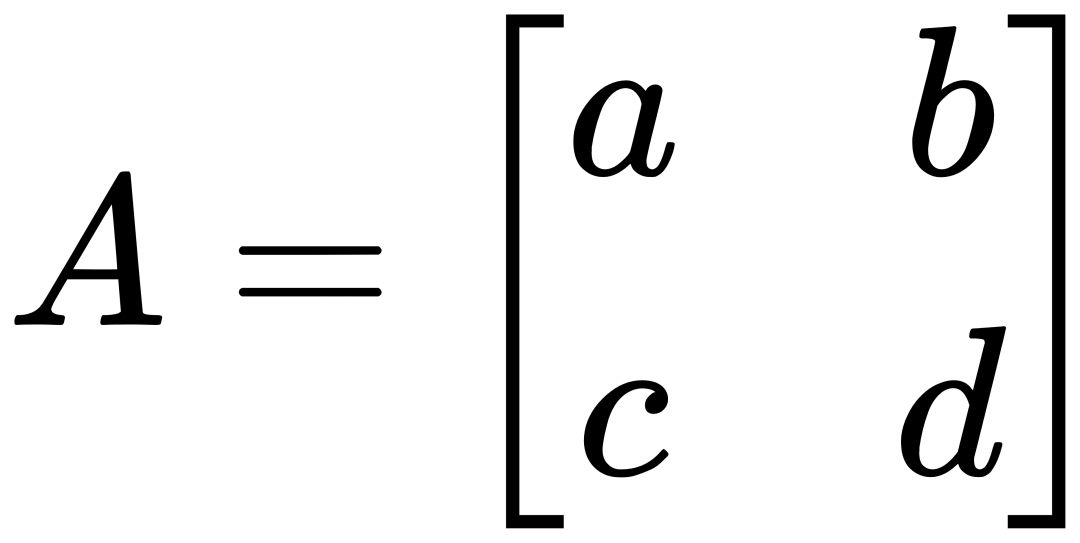
其逆矩阵  A^-1  可以通过以下公式计算：

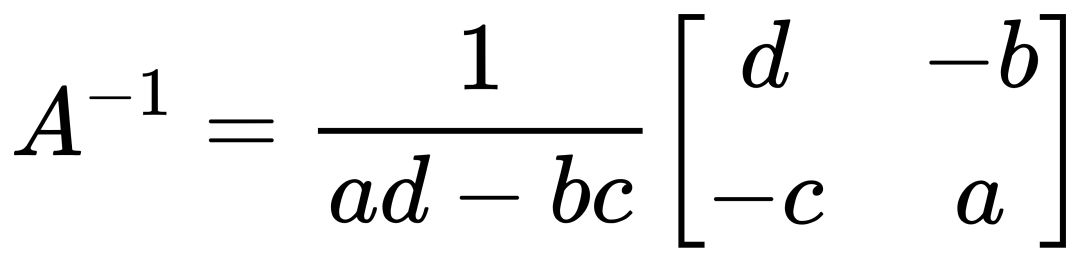
前提是矩阵  A  的行列式不为零。

示例 2：3x3 矩阵

对于矩阵：

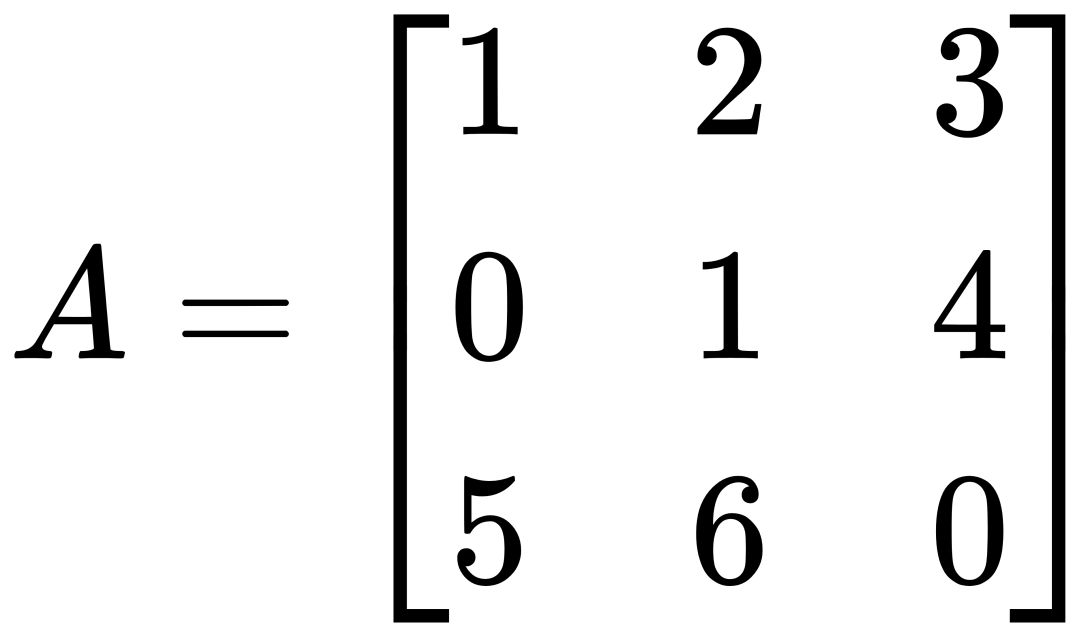
首先计算行列式  det(A) ，然后计算伴随矩阵：

det(A) = 1 x (1 x 0 - 4 x 6) - 2 x (0 x 0 - 4 x 5) + 3 x (0 x 6 - 1 x 5) = 1

行列式计算的方法参考：矩阵行列式怎么求？矩阵行列式计算公式我来告诉你

伴随矩阵  adj(A)  为：

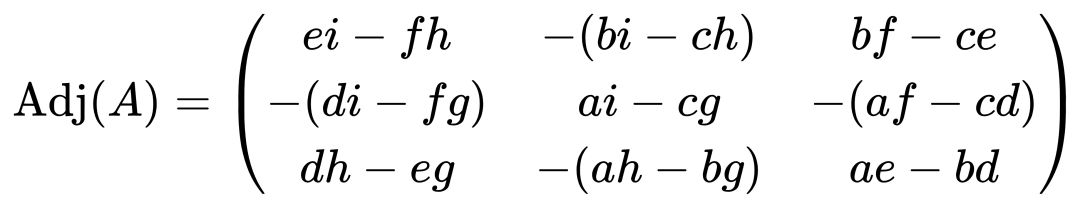
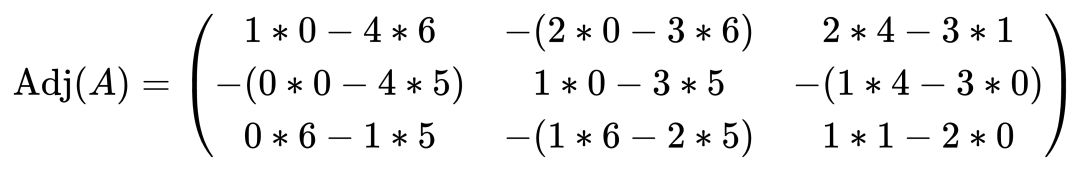
因此，逆矩阵  A^-1  为：

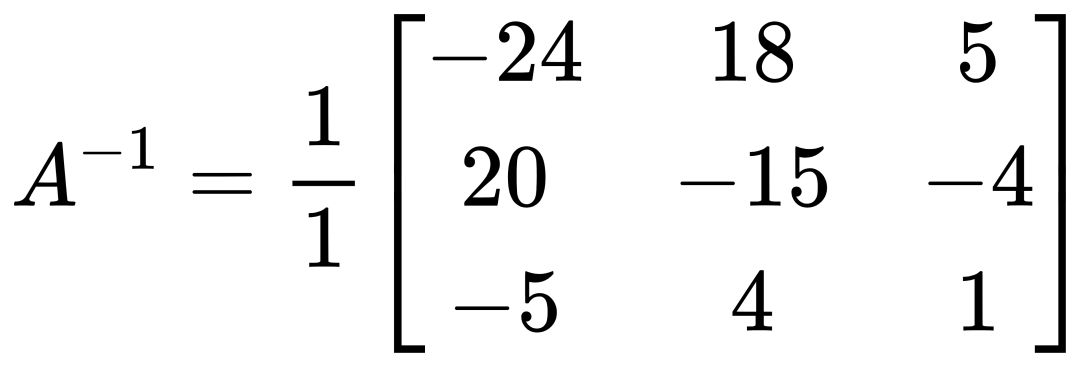
总结

逆矩阵的求法是线性代数中的一个基础且重要的技能。通过高斯-约当消元法或伴随矩阵法，我们可以计算出矩阵的逆。这些方法在解决线性方程组、计算矩阵的方根等方面有着广泛的应用。如果你有任何疑问或需要进一步的帮助，欢迎在下方留言，我们会尽快为你解答。

微信搜一搜【智启创想】，使用逆矩阵计算器