【算法研究】-04-条件随机场

最新推荐文章于 2023-05-26 17:13:54 发布

z.d.k

最新推荐文章于 2023-05-26 17:13:54 发布

阅读量94

点赞数

分类专栏：机器学习

本文链接：https://blog.csdn.net/yiqi1943/article/details/105824118

版权

机器学习专栏收录该内容

2 篇文章 0 订阅

订阅专栏

文章目录

理论部分

相关概念
- 马尔可夫过程
  定义:假设一个随机过程中， $t_n$ 时刻的状态 $x_n$ 的条件发布，只与其前一状态 $x_{n-1}$ 相关，即：
  
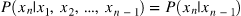
  则将其称为马尔可夫过程。
- 隐马尔科夫算法
  定义：隐马尔科夫算法是对含有未知参数（隐状态）的马尔可夫链进行建模的生成模型，如下图所示：
  
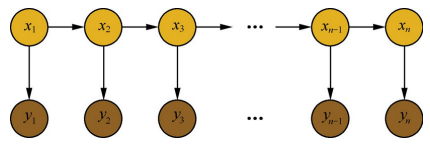
  在隐马尔科夫模型中，包含隐状态和观察状态，隐状态 $x_i$ 对于观察者而言是不可见的，而观察状态 $y_i$ 对于观察者而言是可见的。隐状态间存在转移概率，隐状态 $x_i$ 到对应的观察状态 $y_i$ 间存在输出概率。
  1. 假设隐状态 $x_i$ 的状态满足马尔可夫过程，i时刻的状态 $x_i$ 的条件分布，仅与其前一个状态 $x_{i-1}$ 相关，即：
    $P(x_i|x_1,x_2,...,x_{i-1}) = P(x_i|x_{i-1})$
  2. 假设观测序列中各个状态仅取决于它所对应的隐状态，即：
    $P(y_i|x_1,x_2,...,x_{i-1},y_1,y_2,...,y_{i-1},y_{i+1},...) = P(y_i|x_{i})$
条件随机场
定义：给定 $X=(x_1,x_2,...,x_n)$ ， $Y=(y_1,y_2,...,y_n)$ 均为线性链表示的随机变量序列，若在给随机变量序列 X 的条件下，随机变量序列 Y 的条件概率分布 $P (Y ∣ X)$ 构成条件随机场，即满足马尔可夫性：

$P(y_i|x_1,x_2,...,x_{i-1},y_1,y_2,...,y_{i-1},y_{i+1}) = P(y_i|x,y_{i-1},y_{i+1})$

则称为 P(Y|X) 为线性链条件随机场。

转移特征和状态特征
通过去除了隐马尔科夫算法中的观测状态相互独立假设，使算法在计算当前隐状态 $x_i$ 时，会考虑整个观测序列，从而获得更高的表达能力，并进行全局归一化解决标注偏置问题。

参数化形式
$p\left(y | x\right)=\frac{1}{Z\left(x\right)} \prod_{i=1}^{n} \exp \left(\sum_{i, k} \lambda_{k} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)$
其中：

$Z (x)$ 为归一化因子，是在全局范围进行归一化，枚举了整个隐状态序列 $x_{1…n}$ 的全部可能，从而解决了局部归一化带来的标注偏置问题。
$Z(x)=\sum_{y} \exp \left(\sum_{i, k} \lambda_{x} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)$
- $t_k$ 为定义在边上的特征函数，转移特征，依赖于前一个和当前位置
- $s_1$ 为定义在节点上的特征函数，状态特征，依赖于当前位置。
- 矩阵形式
条件随机场三问题
- 计算问题：已知模型的所有参数，计算观测序列 $Y$ 出现的概率，常用方法：前向和后向算法；
1. 前向计算
  对观测序列 $x$ 的每个位置 $i = 1, 2, . . ., n + 1$ ，定义一个 $m$ 阶矩阵（ $m$ 为标记 $Y_i$ 取值的个数）。
  $M_{i}(x)=\left[M_{i}\left(y_{i-1}, y_{i} | x\right)\right]$
  $M_{i}\left(y_{i-1}, y_{i} | x\right)=\exp \left(W_{i}\left(y_{i-1}, y_{i} | x\right)\right)$
  $W_{i}\left(y_{i-1}, y_{i} | x\right)=\sum_{i=1}^{K} w_{k} f_{k}\left(y_{i-1}, y_{i}, x, i\right)$
  
  对每个指标 $i = 0, 1, . . ., n + 1$ ，定义前向向量 $\alpha_{i}(x)$ ，则递推公式:
  $\alpha_{i}^{\mathrm{T}}\left(y_{i} | x\right)=\alpha_{i-1}^{\mathrm{T}}\left(y_{i-1} | x\right) M_{i}\left(y_{i-1}, y_{i} | x\right), \quad i=1,2, \cdots, n+1$
  其中，
  $\alpha_{0}(y | x)=\left\{\begin{array}{ll}1, & y=\text { start } \\ 0, & \text { 否则 }\end{array}\right.$
2. 后向计算
  对每个指标 $i = 0, 1, . . ., n + 1$ ，定义前向向量 $\beta_{i}(x)$ ，则递推公式:
  $\beta_{n+1}\left(y_{n+1} | x\right)=\left\{\begin{array}{ll}1, & y_{n+1}=\text { stop } \\ 0, & \text { 否则 }\end{array}\right.$
  $\beta_{i}\left(y_{i} | x\right)=M_{i}\left(y_{i}, y_{i+1} | x\right) \beta_{i-1}\left(y_{i+1} | x\right)$
3. ？？？
  $Z(x)=\alpha_{n}^{\mathrm{T}}(x) \cdot \mathbf{1}=\mathbf{1}^{\mathrm{T}} \cdot \beta_{1}(x)$
4. 概率计算
  所以，标注序列在位置 $i$ 是标注 $y_i$ 的条件概率为：
  $P\left(Y_{i}=y_{i} | x\right)=\frac{\alpha_{i}^{\mathrm{T}}\left(y_{i} | x\right) \beta_{i}\left(y_{i} | x\right)}{Z(x)}$
  $P\left(Y_{i-1}=y_{i-1}, Y_{i}=y_{i} | x\right)=\frac{\alpha_{i-1}^{T}\left(y_{i-1} | x\right) M_{i}\left(y_{i-1}, y_{i} | x\right) \beta_{i}\left(y_{i} | x\right)}{Z(x)}$ $P\left(Y_{i-1}=y_{i-1}, Y_{i}=y_{i} | x\right)=\frac{\alpha_{i-1}^{T}\left(y_{i-1} | x\right) M_{i}\left(y_{i-1}, y_{i} | x\right) \beta_{i}\left(y_{i} | x\right)}{Z(x)}$
  其中，
  $Z(x)=\alpha_{n}^{\mathrm{T}}(x) \cdot \mathbf{1}$
5. 期望概率计算
  通过利用前向-后向向量，计算特征函数关于联合概率分布 $P (X, Y)$ 和条件概率分布 $P (Y ∣ X)$ 的数学期望，即特征函数 $f_k$ 关于条件概率分布 $P (Y ∣ X)$ 的数学期望：
  $\begin{aligned} E_{P(Y | X)}\left[f_{k}\right] &=\sum_{y} P(y | x) f_{k}(y, x) \\ &=\sum_{i=1}^{n+1} \sum_{y=1, y_{1}} f_{k}\left(y_{i-1}, y_{i}, x, i\right) \frac{\alpha_{i-1}^{\top}\left(y_{i-1} | x\right) M_{i}\left(y_{i-1}, y_{i} | x\right) \beta_{i}\left(y_{i} | x\right)}{Z(x)} \\ k &=1,2, \cdots, K \end{aligned}$

扁平
$Z(x)=\alpha_{n}^{\mathrm{T}}(x) \cdot \mathbf{1}$
其中，

学习问题：已知观测序列 $Y$ ，求解使得该观测序列概率最大的模型参数，包括隐状态序列、隐状态间的转移概率分布和从隐状态到观测状态的概率分布，常用方法：Baum-Wehch 算法；
预测问题：一直模型所有参数和观测序列 $Y$ ，计算最可能的隐状态序列 $X$ ,常用算法：维特比算法。
维特比算法：
输入：模型特征向量 $F (y, x)$ 和权重向量 $w$ ，输入序列（观测序列） $x={x_1,x_2,...,x_n}$ ；
输出：条件概率最大的输出序列（标记序列） $y^{*}= (y_1^*,y_2^*,...,y_n^*)$ ，也就是最优路径；
1. 初始化
  $\delta_{1}(j)=w \cdot F_{1}\left(y_{0}=\operatorname{start}, y_{1}=j, x\right), \quad j=1,2, \cdots, m$
2. 递推，对i=2，3，…，n
  $\delta_{i}(l)=\max _{1 \leqslant j \leqslant m}\left\{\delta_{i-1}(j)+w \cdot F_{i}\left(y_{i-1}=j, y_{i}=l, x\right)\right\}, \quad l=1,2, \cdots, m$
  $\Psi_{i}(l)=\arg \max _{1 \leq j \leqslant m}\left\{\delta_{i-1}(j)+w \cdot F_{i}\left(y_{i-1}=j, y_{i}=l, x\right)\right\}, \quad l=1,2, \cdots, m$
3. 终止
  $\max _{y}(w \cdot F(y, x))=\max _{1 \leq j \leq m} \delta_{n}(j)$
  $y_{n}^{*}=\arg \max _{1 \leq j \leqslant m} \delta_{n}(j)$
4. 返回路径
  $y_{i}^{*}=\Psi_{i+1}\left(y_{i+1}^{*}\right), \quad i=n-1, n-2, \cdots, 1$

练习部分

利用高维特比算法计算给定输入序列 ${x}$ 对应的最优输出序列 $y^{*}$
$\max \sum_{i=1}^{3} w \cdot F_{i}\left(y_{i-1}, y_{i}, x\right)$
维特比：
高维特比：

初始化
$\delta_{1}(j)=w \cdot F_{1}\left(y_{0}=\text {start}, y_{1}=j, x\right), \quad j=1,2$
$\quad \delta_{1}(1)=1, \quad \delta(2)=0.5$
递推，对i=2,3,…n
$i = 2$
$\delta_{2}(l)=\max _{f}\left\{\delta_{1}(j)+w \cdot F_{2}(j, l, x)\right\}$
$\delta_{2}(1)=\max \left\{1+\lambda_{2} t_{2}, 0.5+\lambda_{4} t_{4}\right\}=1.6, \quad \Psi_{2}(1)=1$
$\delta_{2}(2)=\max \left\{1+\lambda t_{1}+\mu_{2} s_{2}, 0.5+\mu_{2} s_{2}\right\}=2.5, \quad \Psi_{2}(2)=1$
$i = 3$
$\delta_{3}(l)=\max _{j}\left\{\delta_{2}(j)+w \cdot F_{3}(j, l, x)\right\}$
$\delta_{3}(1)=\max \left\{1.6+\mu_{5} s_{5}, 2.5+\lambda_{3} t_{3}+\mu_{3} s_{3}\right\}=4.3, \quad \Psi_{3}(1)=2$
$\delta_{3}(2)=\max \left\{1.6+\lambda_{1} t_{1}+\mu_{4} s_{4}, 2.5+\lambda_{5} t_{5}+\mu_{4} s_{4}\right\}=3.2, \quad \Psi_{3}(2)=1$
终止
$\max _{y}(w \cdot F(y, x))=\max \delta_{3}(l)=\delta_{3}(1)=4.3$
$y_{3}^{*}=\arg \max _{l} \delta_{3}(l)=1$
返回路径
$y_{2}^{*}=\Psi_{3}\left(y_{3}^{*}\right)=\Psi_{3}(1)=2$
$y_{1}^{*}=\Psi_{2}\left(y_{2}^{*}\right)=\Psi_{2}(2)=1$
求得最优路径 $y^{*}= (y_1^*,y_2^*,...,y_n^*) = (1,2,1)$

z.d.k

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【算法研究】-04-条件随机场

文章目录理论部分相关概念马尔可夫过程定义:假设一个随机过程中，tnt_ntn 时刻的状态xnx_nxn的条件发布，只与其前一状态xn−1x_{n-1}xn−1 相关，即：则将其称为马尔可夫过程。隐马尔科夫算法定义：隐马尔科夫算法是对含有未知参数（隐状态）的马尔可夫链进行建模的生成模型，如下图所示：在隐马尔科夫模型中，包含隐状态和观察状态，隐状态 xix_...
复制链接

扫一扫