一.协同过滤算法(Collaborative Filtering)
1.简介
协同过滤算法:是一种基于群体用户或者物品的经典推荐算法。分两种:
(1).通过考察具有相同爱好的用户对相同物品的评分标准进行计算。
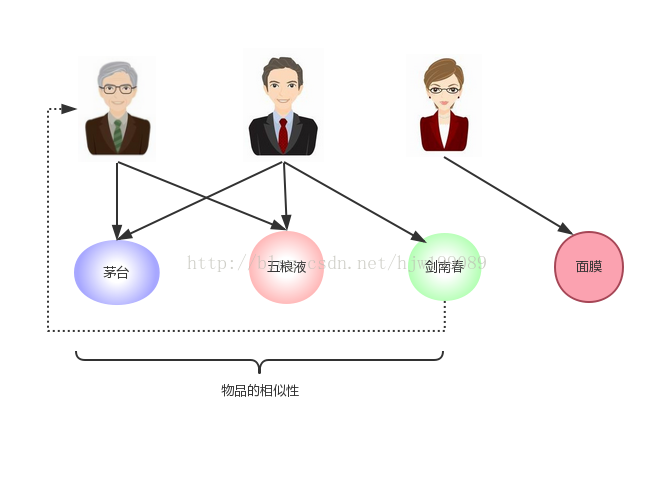
(2).考察具有相同特质的物品从而推荐给选择了某件物品的用户。
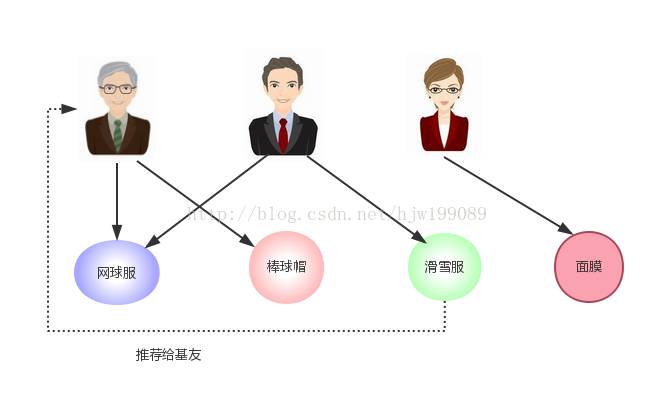
A和B是“志同道合”的基友(相似度很高),将A喜欢的物品推荐给B是合理的
在无先验知识的前提下,根据A所喜欢物品的相似性,将相似物品推荐给A,是合理的
2.问题
基于用户,数据量大,对于通用物品往往优先推荐,对于热点物品不够准
基于物品,数据量相对小,而推荐同类物品存在用户已持有不再需要的问题
二.相似度度量
1.基于欧几里得距离的相似度计算
(1)欧几里得距离(Euclidean distance):表示三维空间中两个点的真实距离。是一种基于用户之间直线距离的计算方式。
不同的物品或用户对应不同的坐标,特定目标定位为坐标原点。
欧几里得距离公式:

相似度:1/(d+1)
2.基于余弦角度的相似度计算
特定目标作为坐标上的点,但不是原点。夹角的大小来反映目标之间的相似度。
3.欧几里得相似度与余弦相似度的比较
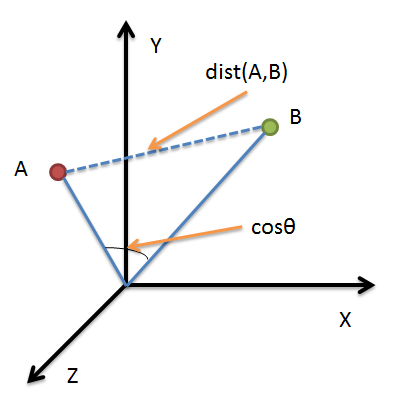
欧几里得相似度注重目标之间的差异。
余弦相似度更多是对目标从方向趋势上区分。
4.余弦相似度实战
/** * Created by Administrator on 2017/4/17. */ import org.apache.spark.{SparkConf, SparkContext} import scala.collection.mutable.Map object testVector { val conf = new SparkConf() .setMaster("local") .setAppName("testVector"); val sc = new SparkContext(conf); //将内存数据读入Spark系统中 val users = sc.parallelize(Array("aaa","bbb","ccc","ddd","eee")); val films = sc.parallelize(Array("smzdm","ylxb","znh","nhsc","fcwr")); //使用一个source嵌套map作为姓名,电影名和分值的评价 var source = Map[String,Map[String,Int]](); //设置一个用于存放电影分的map val filmSource = Map[String,Int](); //设置电影评分 def getSource(): Map[String,Map[String,Int]] = { val user1FilmSource = Map("smzdm" -> 2,"ylxb" -> 3,"znh" -> 1,"nhsc" -> 0,"fcwr" -> 1); val user2FilmSource = Map("smzdm" -> 1,"ylxb" -> 2,"znh" -> 2,"nhsc" -> 1,"fcwr" -> 4); val user3FilmSource = Map("smzdm" -> 2,"ylxb" ->








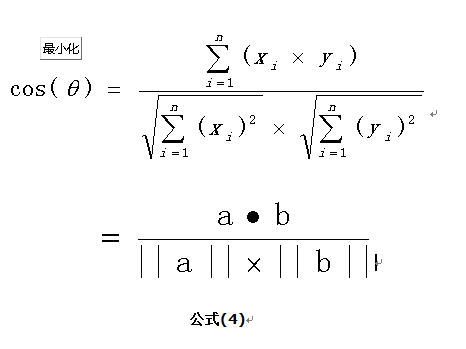
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 7889
7889











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








