第三章 词法分析

3.1词法分析器的设计

词法分析的主要工作:
       从源程序的第一个字符开始，从左到右扫描源程序，一次读一个字符，根据词法规则将有关字符组合成单词，并识别各类单词，当确定单词类别后，将单词输出。

在词法分析过程中还要完成其它任务，如：
• 过滤掉源程序中的注释和空白；
• 记录读入字符的行号，以便发现错误后能报告出错位置；
• 进行预编译工作 ( 对宏进行展开 等工作 ) ；
• 符号表操作。
• 错误处理等。
词法分析与语法分析的接口方式：

(1)词法分析作为一遍：

将词法分析器的输出结果放入一个中间文件上(外存)或直接存放在内存中，后面的语法分析程序将它作为输入进行语法分析，这样通过一遍加工就可以将以字符串形式的源程序加工成单词串形式的源程序。

(2)词法分析与语法分析安排在同一遍中：

将词法分析编成一个子程序，该子程序由语法分析程序调用。当语法分析程序需要一个新单词时，调用该程序，每调用一次，则从源程序中读出一个单词，这样避免了中间文件的生成，可以提高编译效率。

词法分析的分离：

实际上， 词法 也是 语法 的一部分，词法描述完全可
以归并到语法描述中去，只不过词法规则更简单些。进
一步说，在编译程序中可以将词法分析包含在语法分析
之中，那么为什么把编译过程的分析工作划分成词法分
析和语法分析两个阶段？主要考虑的因素为：
(1) 使整个编译程序的结构更简洁、清晰和条理化；
(2) 编译程序的效率会改进；
(3) 增强编译程序的可移植性。

源程序的输入：

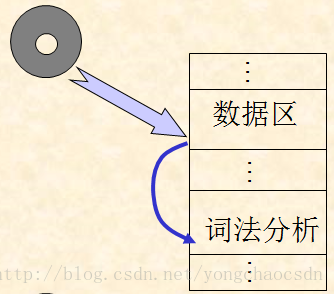
(1)一次性输入：当内存较大时，把源程序一次性输入到内存的用户数据区，每个字符占一个字节，词法分析程序从数据区中依次读入字符。

(2)分批次输入：当内存不够大时，在内存开辟一个适当大小的输入缓冲区，输入时，把源程序分批输入到输入缓冲区，词法分析程序从缓冲区中读取字符，当缓冲区的字符全部读完以后，再从外存上读入下一批，直到全部源程序字符读完为止。

(3)超前搜索：词法分析程序在组合单词的时候，为了进一步判明情况和确定下一步要做什么以及为了处理上的方便等，常采取超前搜索的办法，即先向前读取字符和判别字符是什么，不马上处理，当情况判明后，再回来处理已读过的字符。

例如：有源程序，function example(input,output);

在判别保留字function过程中，当读到字符n时，虽然前
面字符为function ，还要看是否结束，即后面字符是什么
(字母、数字还是空格)，所以不能马上处理(断定是保留
字)，而需要再向前读一个字符，确定后再回来处理。

在判别标识符example过程中，当读到字符e时，虽然前
面字符为example，为了判别下一个字符是否是该标识符
的一部分，也要判别下一个字符是否为字母或数字，所
以不能马上处理，需要再向前读一个字符。

有时，为了判别读进字
符所组成的单词的类别，
需向前读若干字符！

(4)扫描缓冲区的处理：显然，无论缓冲区设定为多大，都不能保证单词不会被它的边界打断，若有单词TEST123，可能在缓冲区中成为：

在这种情况下，即使搜索指针读到缓冲区的最后一个字符，但仍不能找到该单词的右边界，这时，若从外存上再读一部分源程序进入缓冲区，则会将没有处理过的字符(TES)冲掉。为此，我们可将缓冲区分成相等的两个区域：

单词的输出：

(1)单词的种类：

保留字：如，program begin end var const for ……

标识符：如，程序名、变量名、常量名、类型名、过程名等

常数：如，125、0.745、15.2E+5

算符 ：如，+、– 、*、/、等

界符：如，分号、逗号等

(2)词法分析器的输出形式：

为了便于编译程序进一步加工，单词的输出形式一般采用二元式：

采用什么样的输出形式也是取决于后续处理的方便，如：

• 标识符用字符串编码或对应地址；

• 常数用其自身值的二进制形式；

• 保留字(分界符)若将全体定位一类则需输出其值，可用内部整数编码或串编码表示。

用整数编码表示，如何分类以处理方便为原则，如：

• 标识符归为一类；

• 常数按类型分类；

• 保留字一字一类，或将全体定位一类；

• 界符可单独作为一类，或一符一类。

例如：程序段  if i=5 then x ：= y；在经过词法分析器扫描后，输出的单词可表示如下：

            保留字if              (3，‘if’)
            标识符i               (1，指向i的符号表入口)
            等号=                  (4，‘=’)
            常数5                   (2，‘5’的二进制表示)
            保留字then          (3，‘then’)
            标识符x               (1，指向x的符号表入口)
            赋值号:=             (4，‘：=  ’)
            标识符y               (1，指向y的符号表入口)
            分号；                 (5，‘；’)

其中，类别码：“1”表示标识符；“2”表示常数；
         “3”表示保留字；“4”表示算符；“5”表示界符。

3.2正则文法与状态转换图

一、状态转换图

       许多程序设计语言的单词，可以用正则文法来描述。对于这样的语言，使用状态转换图可以设计词法分析程序（扫描器）。状态转换图TG（简称状态图或转换图）是一张定义在字母表Σ上的有限方向图。 

在状态转换图中:

• 结点代表 状态 ，用圆圈表示；

• 状态之间用 有向弧 连结；

• 有向 弧上的标记 （字符）表示在射出结点（有向弧的开始结点）所代表的状态下可能出现的输入符号或符号串。

• 用带有符号“=> ”的圆圈表示状态转换图的 初始状态

    一个状态转换图可用于接受（或识别）一定的符号串。在状态转换图中从初始状态到某一终止状态的序列为路。对于某一符号串β，在状态转换图中，若存在一条路产生β，则称状态转换图接受（或识别）该符号串β，否则符号串β不能被接受。能被状态转换图TG接受的符号串的集合记为L(TG)，称为状态转换图所能识别的语言。

    由以上状态转换图可见，字母表Σ上的符号串：      

01 10 0100 0111 1011
010011 011100 „„
都能被上述转换图所接受。
即有： L(TG)={ 01 ， 10 ， 0100 ， 0111 ， 1011 ， 010011 ，
011100 ， „ „ }

再如，设有字母表Σ={a,b}，则有字母表Σ上的一个状态转换图如下：

由转换图可见，字母表Σ={a,b}上的符号串：

    a，b，ab，ba，aaa，bbb，aab，bba，…均能被这个转换图所接受。

从而有：L(TG)={ a，b，ab，ba，aaa，bbb，aab，bba，…}

二、正则文法的状态转换图表示

       许多程序设计语言的单词可以用正则文法来表示，而对于正则文法所描述的语言又可以用状态转换图来非形式的表示。

对于右线性文法G[S]

U→xV|y

， 状态转换图的表示方法如下：

(1)用状态表示G[S]中的非终结符，G[S]的开始符号S对
应状态转换图的开始状态S；
(2)增加一个新状态Z， 作为状态转换图的终止状态；
(3)对于G[S]中形如U→xV的每条产生式，画一条从状态
U到状态V的方向弧，弧上的标记为x；
(4)对于G[S]中形如U→y的每条产生式，画一条从状态U
到终态Z的方向弧，弧上的标记为y

例如：给出与正则文法G(S)等价的状态转换图。

G[S]： 

S→aA S→bB S→ε A→aB A→bA B→aS B→bA B→ε

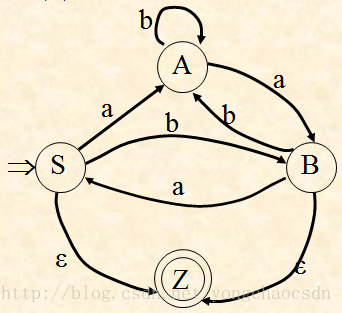
        正则文法与状态转换图等价，是指正则文法所确定的语言L(G)，与状态转换图所接受的语言L(TG)相同：
         L(G)=L(TG)

对于左线性文法G[Z]

U→Vx|y

， 状态转换图的表示方法如下： (1) 用 状态 表示 G[Z] 中的 非终结符 ， G[Z] 的 开始符号 Z 对
应状态转换图的 终止状态 Z
(2) 增加一个 新状态 S ， 作为状态转换图的 初始状态 ；
(3) 对于 G[Z] 中形如 U→Vx 的每条产生式，画一条从状态
V 到状态 U 的方向弧，弧上的 标记为 x ；
(4) 对于 G[Z] 中形如 U→y 的每条产生式，画一条从 初态 S
到状态 U 的方向弧，弧上的 标记为 y
例如 ：给出与正则文法 G[Z]
等价的状态转换图
G[Z]: Z→U0 |V1
U→Z1 |1
V→Z0 |0

右线性文法状态图的识别过程，是为串w建立
一个推导S =>*w的过程。
• 左线性文法状态图的识别过程，是从串w出发的归约
过程，最后归约为开始符号S（终态）。

3.3正规表达式与有限自动机

3.3.1 正规式和正规集

       为了识别正则语言，我们引入了状态转换图和有限自动机，有限自动机所接受的语言正是正则文法产生的语言(正则语言)，程序设计语言中的单词也大多是由正则文法产生的。作为单词的语法除了用正则文法描述外，我们还可以用一种更有效的工具——正规式加以描述。

正规式和正规集的定义

     多数程序设计语言的单词的语法都能用正规文法来表示。即文法G=(VN,VT,S,Z)中的规则P都有下述形式：A→aB或A→a，其中A,B∈VN，a∈VT。

      实际上，正规文法所描述的是字母表Σ上的一些特殊子集，称为正规集。

例如，标识符可用下述规则描述：

  <标识符>→l|l<字母数字>

  <字母数字>→l|d|l<字母数字>|d <字母数字>

  其中l表示a～z中的任何一英文字母，d表示0～9中的任一数字。从中我们可以知道标识符是由一个字母之后跟随若干个字母或数字组成。

正规式也称 正则表达式 ，是用于描述单词的另外一个工具，也是表示正规集的工具。下面我们给出正规式和它所表示的正规集的递归定义：

设有字母表为Σ，
(1)ε和ф是Σ上的正规式，它们所表示的正规集分别为{ε}和ф;
(2) 若a∈Σ， 则a是Σ上的正规式，它所表示的正规集为{a};
(3)若e1和e2都是Σ上的正规式，且它们所表示的正规集分别为
L(e1)和L(e2)， 那么：
(e1) 是正规式，表示的正规集为L(e1)；
e1|e2 是正规式，表示的正规集为L(e1)∪L(e2)；
e1·e2是正规式，表示的正规集为L(e1)L(e2)；
e1* 是正规式，表示的正规集为(L(e1))*。
(4)仅由有限次使用上述三步骤而定义的表达式才是Σ上的正规
式，仅由这些正规式所表示的字集(符号串集合)才是Σ上的正
规集。
其中: “|”读为“或”；
“·”读为“连接”；
“* ”读为“闭包”(即，任意有限次的自重复连接)。
算符的优先级为先“* ”，再“·”最后“|”,都是左
结合的，它们满足结合律，规定了算符的优先级后，可以
省去一些不必要的括号:

例如，正规式(a)| ((b) * (c))可以表示成a|b*c，它所表示的正规集为：串a或者是零个或多个b后跟随一个c

例如：令Σ={a,b},Σ上的正规式和相应的正规集的例子有：
     正规式              正规集
        a|b                 {a,b}
     (a|b)(a|b)           {aa,ab,ba,bb}
         a*                  0个或多个a的串所组成的集合
        (a|b) *             {a,b}*即a和b所能构成的所有串的集合

例如：令Σ={d , e , + ,-,.}， 其中d为0～9中的数字，问：Σ
上的正规式 d*(.dd*|ε)(e(+|-|ε)dd*|ε)表示的语言是什么？
它所表示的语言(正规集)为无符号数。
如果两个正规式r和s表示同样的正规集，我们称两个正规
式r和s等价，写作r=s。例如，若Σ={a,b}， 则它上面的正规式
a|b和b|a表示的正规集都是{a,b}， 因此是等价的正规式。
而对某个正规式来说，可以对其进行变换并使它表示的
正规集不变，这样的变换称为等价变换，在等价变换的过程
中，正规式服从以下代数定律：
设r，s，t为正规式，则:

1． r|s=s|r	“ | ”运算满足交换律
2． r|(s|t)=(r|s)|t	“ | ”运算的可结合律
3． (rs)t=r(st)	“连接”运算的可结合律

4 ． r(s|t)=rs|rt (s|t)r=sr|tr 分配律
5 ．  ε r = r rε= r ε 是“连接”的恒等元素
6 ． r* = (r| ε )* ε 和 * 的关系
7 ． ( r*)* = r* * 是幂等的

3.3.2 有限自动机

确定的有限自动机(Deterministic Finite Automata)

例如：为下图所示的状态图构造确定的有限自动机。

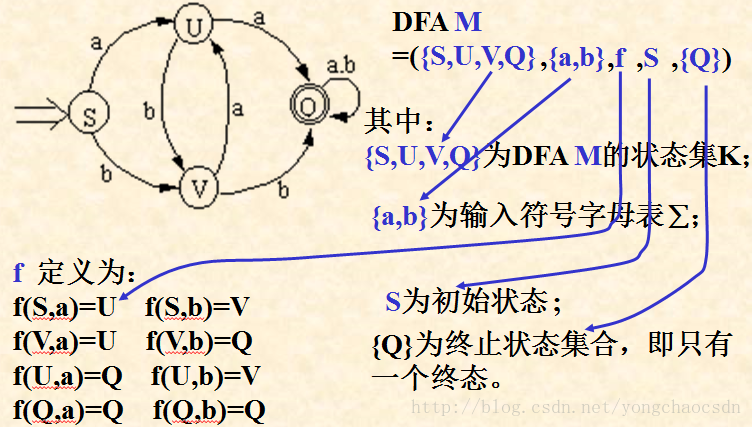
      事实上，状态转换图是有限自动机的一种表示形式,假定DFAM含有m个状态，n个输入字符，那么这个状态转换图含有m个状态（结点），每个结点最多有n个弧射出，整个图含有唯一一个初态结点(冠以“=>”)和若干个终态结点(用双圈表示 )，若有f(ki,a)=kj(ki∈K,kj∈K，a∈Σ)，则从状态结点ki到状态结点kj画标记为a的弧。 

   一个DFA还可以用一个矩阵(状态矩阵）表示：矩阵的行表示状态，列表示输入字符，矩阵元素表示相应状态行和输入字符列下的新状态。

例如：上例的DFA的矩阵表示如下：

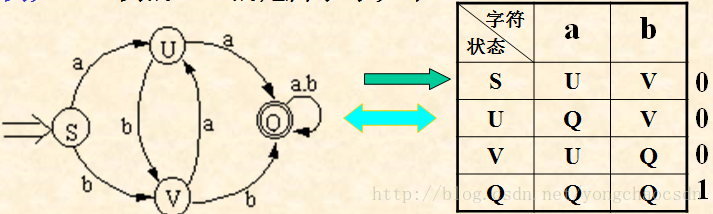
第一行表示初态

相应终态行在右端标以1，
非终态标以0

       对于Σ*中的任何字符串α,若DFA M中存在一条从初态结点到某一终态结点的路,且这条路上所有弧的标记连接成的字符串等于α，则称α可以被DFA M所接受(识别)。

      若M的初态结点同时又是终态结点，则空串ε可被M所接受（识别）。

      若α∈Σ*，f(S0, α)=P，其中S0为DFA M的初始状态，P∈Z，Z为终态集。则称字符串α可以被DFA M所接受(识别)

       DFA M所能识别的所有字符串的全体（字的全体）称为DFA M所能接受的语言，记为L(M)

为了加深对上述定义的理解，我们给出扩充的转换函数的定义：

f(q, ε)=q ，其中q∈S，即q为任意状态；f(q,Tα)=f(f(q,T), α),其中T∈Σ, α∈Σ*。 

举例：试证baab可被下面的DFA所接受。

因为： f(S ,baab)
=f(f(S,b),aab)=f(V , aab)
=f(f(V,a),ab) =f(U , ab)
=f(f(U,a) , b) =f(Q ,b)=Q
Q属于终态，得证
可以看出：这个定义使得转换函数的定义域从原来的
S×Σ扩充到S×Σ*上，即f成为从S×Σ*到S的映象。
DFA的确定性表现在转换函数f: S×Σ→S是一个单值函
数， 也就是说对任何状态k∈S,和输入符号a∈Σ，f(k,a)唯
一地确定了下一个状态。
从状态转换图来看， 若字母表含有n个输入字符， 那么
任何一个状态结点最多有n条弧射出， 而且每条弧以一个
不同的输入字符进行标记。
非确定的有限自动机(Nondeterministic Finite Automata)
一个非确定的有限自动机(NFA) M是一个五元组：
M=(S ，Σ，f，S0，F)， 其中
(1) S是一个非空有限集，它的每个元素称为一个状态；

(2)Σ是一个有限的输入字母表，它的每个元素称为一个输入字符;

(3) f是转换函数，它是从S ×Σ*到2S的映象

(4)S0<(包含于)S是一个非空的初始状态集；
(5)F <(包含于)S， 是终止状态集合
所以，一个含有m个状态和n个输入字符的NFA可表示
成如下的一张状态转换图：这张状态转换图含有m个状态结
点，每个结点可射出若干条箭弧与别的结点相连接，每条弧
用Σ*中的一个串作标记(可相同)，整个图至少含有一个初态
结点以及若干个终态结点。

例如 ： 一个 NFA M=({0,1,2,3,4},{a,b},f,{0},{2,4})
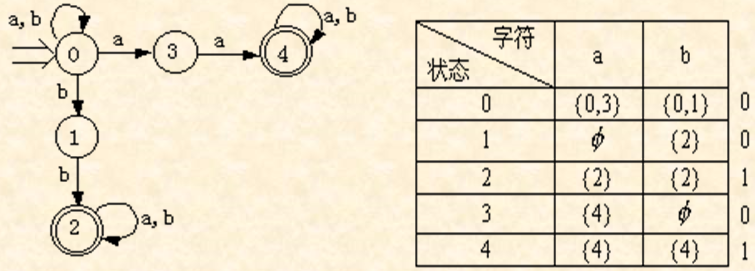
f(0,a)={0,3} f(0,b)={0,1}
f(1,b)={2} f(2,a)={2}
f(2,b)={2} f(3,a)={4}
f(4,a)={4} f(4,b)={4}
其中：

那么，它的状态转换图表示为： 它的矩阵表示为：

跟DFA有相似的结论：对于Σ*中的任何一个串α，若NFA M中存在一条从某一初态结点到某一终态结点的路，且这条路上所有弧的标记依次连接成的串（不理睬那些标记为ε的弧）等于α，则称α可以被NFA M所接受（识别）。若M的某些结点既是初态结点又是终态结点，或者存在一条从某个初态结点到某个终态结点的ε路，那么空串ε可被M所接受（识别）。

       可以看出，DFA是NFA的一个特例。并且可以证明，对于每个NFA M存在一个DFA M’使得 L(M)=L(M’)。

对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’是等价的。

非确定的有限自动机的确定化

   将有限自动机用计算机程序表示出来，就能实现对词法的分析；

前面说过：“对于每个NFA M存在一个DFA M’使得L(M)=L(M’) ”

就是说：设L为一个由非确定有限自动机接受的集合（语言），则存在一个接受L的确定的有限自动机。下面给出从NFA构造识别同样语言的DFA的算法。

子集构造法 ：——将NFA的一个状态子集在DFA中用一个状态表示出来。

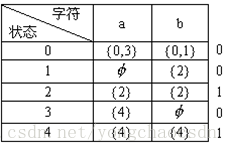
从NFA的矩阵表示中可以看出，表项通常是一个状态的集合，而在DFA的矩阵表示中，表项是一个状态 。

NFA到相应的DFA的构造的基本想法是让DFA的每个状态代表NFA的一个状态集合。

   即在转换后的DFA中，使用它的状态去记录在NFA中读入一个输入符号后可能到达的所有状态。

   换句话说，在得到的DFA中若输入符号串a1a2…an后，到达某个状态，那么该状态表示对应的NFA的状态集的一个子集，这个子集是NFA在输入符号串a1a2…an后可以到达的那些状态组成的集合。

首先介绍两个重要运算：

(1)状态集的ε-闭包：状态集I中的任何状态s经任意条ε弧而能到达的所有状态的集合，定义为状态集I的ε-闭包，表示为ε-closure(I)。

(2)状态集的a弧转换：状态集I中的任何状态s经过一条a弧而能到达的所有状态的集合，定义为状态集I的a弧转换，表示为move(I,a)。

     对于任意 NFA M=(K，Σ，f，S，F)，I<(包含于)K，a∈Σ不妨设I={s1,s2,…sj}，

则move(I,a)=f(s1,a)∪f(s2,a) ∪…∪f(sj,a)

(3)状态集的a弧转换的闭包Ia

          Ia= ε-closure(move(I,a))

例如：有下图所示的NFA,我以它为例来说明以上两个运算 。

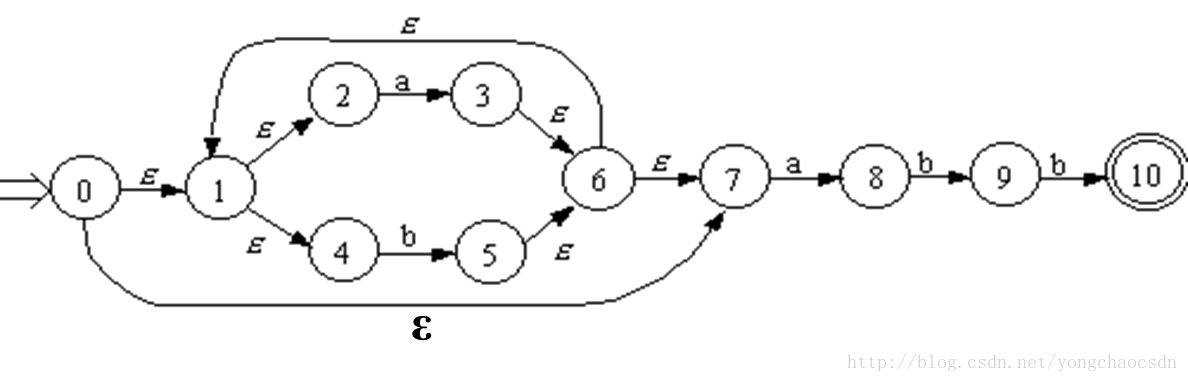
对于I={0}，ε-closure(I)=ε-closure({0})={0,1,2,4,7}；

同理若 I={2,3},ε-closure(I)=ε-closure({2,3})={1,2,3,4,6,7}；

令A={0,1,2,4,7}

则move(A,a)={3,8}

move(A,b)={5}

 同样可以求出其它状态集的ε-闭包和a弧转换

•NFA确定化为DFA的子集法：   
构造下列正规式相应的DFA

1(0|1)*101

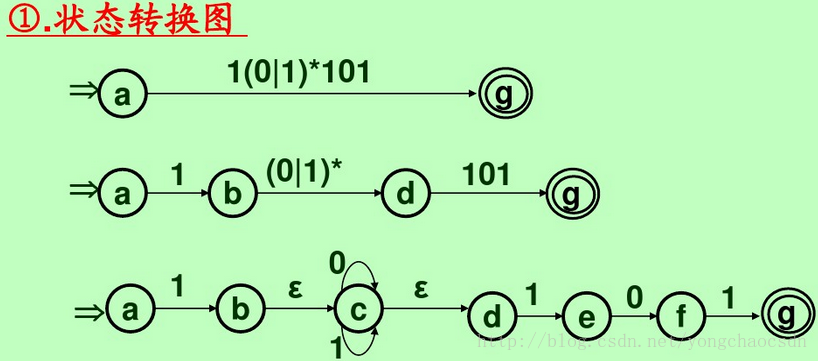
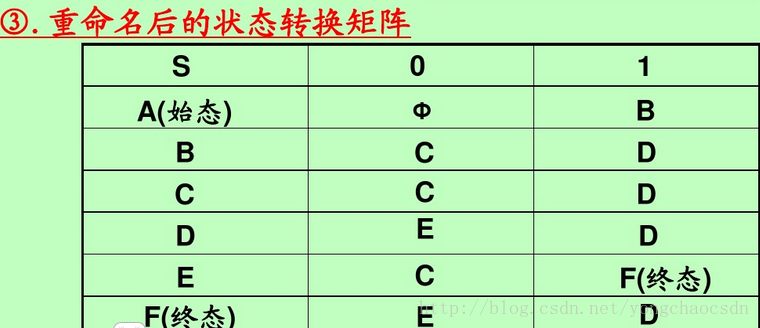
3.3.6确定的有限自动机的最简化(最小化)

      对任意一个DFA M构造另一个DFA M’，使L(M)=L(M’)，并且M’的状态个数不多于M的状态个数。

首先我们介绍几个有关的概念：

(1)多余状态:对于一个状态Si，若从开始状态出发，不可能到达该状态Si，则Si为多余(无用)状态。

(2)死状态:对于一个状态Si，对任意输入符号a，若转到它本身后，不可能从它到达终止状态，则称Si为死状态。

多余状态和死状态又称为无关状态。

S1，S5，S6为多余状态

(3)等价状态:
        若Si为自动机的一个状态，我们把从Si出发能导出的所有符号串集合记为L(Si) 

设有两个状态Si和Sj,若有L(Si)=L(Sj),则称Si和Sj是等价状态。

从S1和S2能导出相同的符号串集合：L(S1)=L(S2)={b}，所以S1和S2等价

(4)可区别状态:自动机中两个状态Si和Sj，如果它们不等价，则称它们是可区别的。

(5)两个状态(Si和Sj)等价的判断条件:

①状态Si和Sj必须同时为终止状态或同时为非终止状态。即终止状态和非终止状态是可区别的； 如，S0，S1，S2肯定与S3不等价

②状态Si和Sj对于任意输入符号a∈Σ，必须转到等价的状态里，否则Si和Sj是可区别的。

因f(S0,b)=S2，f(S2,b)=S3，而S2和S3不等价，故S0和S2也不等价

DFA的化简算法：对于DFA M=(S,Σ,f,S0,Z)
(1)首先将DFA的状态集进行初始化，分成Π=(Z,S-Z);
(2) 用下面的过程对Π构造新的划分Π new
for (Π中每个组G) do //每个组都是一个状态集
begin
把G划分成小组， G中的任意两个状态Si和Sj在同一组中，
当且仅当对于Σ中任意输入符号a， Si和Sj的a转换是到同
一组中， move(Si,a) ∈Gi ， move(Sj,a) ∈Gi。 这样，只要
S
i和Sj的a转换是到不同的组中，则说明Si和Sj是可区别的，
可进行划分。
在Π new中用刚完成的对G的划分代替原来的G。
end ;
Π := Π
new；
(3)重复执行(2)，直到Π中每个状态集不能再划分(Π new= Π)为止;
(4)合并等价状态 ,在每个G中，取任意状态作为代表，删去其它状态;
(5)删去无关状态，从其它状态到无关状态的转换都成为无定义。
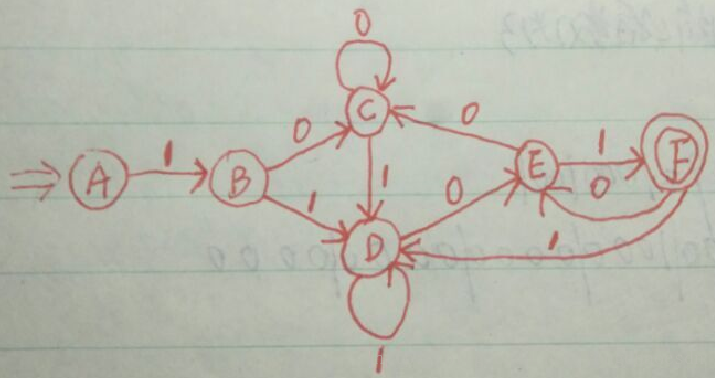
例题 ：将下图所示的 DFA M 最小化

①首次划分: Π0=({1,2,3,4},{5,6,7})

②在G={1,2,3,4}中:
f(1,a)=6，f(2,a)=7(转向终态)；f(3,a)=1,f(4,a)=4(转向非终态)，故{1,2}和{3,4}是可区别的，得Π1=({1,2}，{3,4}，{5,6,7})；

③在G={1,2}中，f(1,a)=6, f(2,a)=7(转向终态子集),而f(1,b)=f(2,b)=3,所以不可区别，不再进行划分；

④考察G={3,4}，f(3,a)=1,f(4,a)=4,可见它们转向Π1的不同组，故得新的划分Π2=({1,2},{3,},{4}{5,6,7})；

⑤对{1,2}重新进行考察，发现它不能进行划分，而{3}和{4}已经最小也不能划分了；

⑥考察G={5,6,7}，因f(5,b)转向{3}，而f(6,b)和f(7,b)转向{1,2}，可得新划分Π3=({1,2},{3},{4},{5},{6,7})；

⑦进一步进行考察，可以发现每个子集都不能再划分了；

⑧消去等价状态：{1,2}用1表示，{6,7}用6表示，得到得新DFA M’如右图所示

⑨去掉无关状态，因DFAM’中没有无关状态，所以右图即为最后结果。

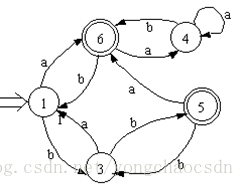
正规式与有限自动机
正规式是单词的一种描述工具，而有限自动机是单词的
识别装置，正规式和有限自动机之间可以相互转换，也就是
说它们之间存在着等价性，主要表现在以下两个方面：
(1) 对于Σ上的NFA M， 可以构造一个Σ上的正规式R， 使得：
L(R)=L(M) ；
(2) 对于Σ上的每个正规式R， 可以构造一个Σ上的NFA M，
使得： L(M)=L(R) 。

 NFA M转化为正规式R： 为了实现为Σ上的NFA M构造
一个等价的正规式R， 我们把状态转换图的概念拓广， 使状
态转换图的每条弧可以用一个正规式作标记， 具体如下：
(1) 在NFA M的状态转换图上加进两个结点x、 y， 从x结点用ε弧连
接到M的所有初态结点，同时从M的所有终态结点用ε弧连接到y结
点，形成一个与M等价的NFA M，， M只有一个初态结点x， 一个
终态结点y ;
(2) 逐步消去M?的结点，直至只剩下x和y两个结点为止。在消结点
过程中，逐步使用正规式来标记弧。使用的规则如下：

按以上规则消结直到最后成为：

例: 对下图所示的NFA M求正规式R，使L(R)=L(M)。

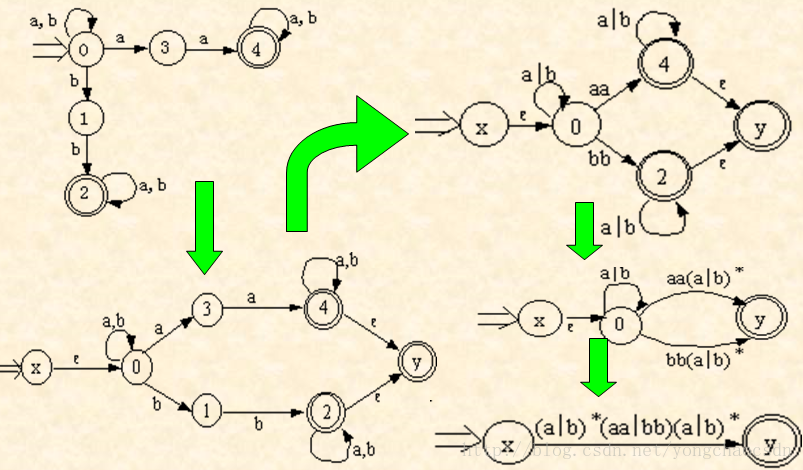
正规式R转化为NFA M：在这个方法中按正规式的语法结构指引构造过程，将正规式分解为一系列子表达式，然后将子表达式对应的NFA依次连接而成，构造规则如下：

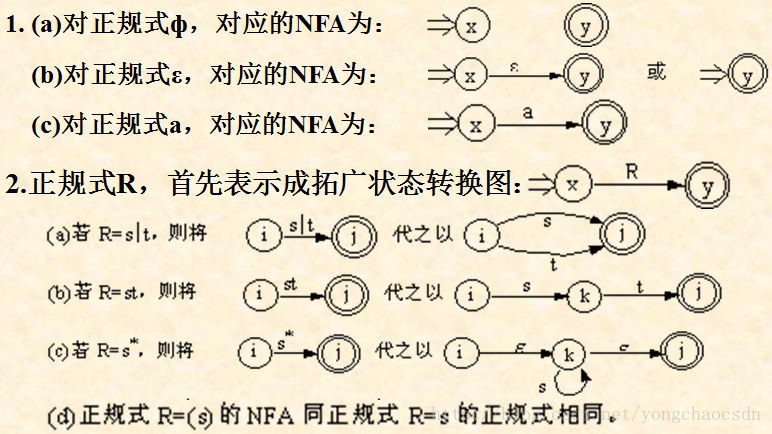
例如：  设有正规式R=(a|b) *abb，试构造NFA N，使得L(N)=L(R)

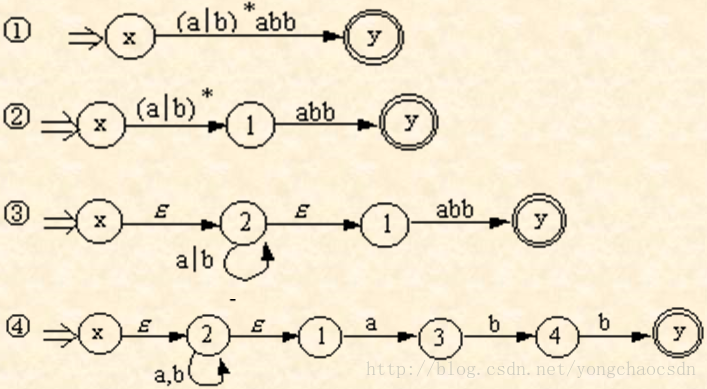
2.6令文法G6为    N -> D|ND

                          D->0|1|2|3|4|5|6|7|8|9

      (1) G6的语言L(G6)是什么？

      (2) 给出句子0127、34和568的最左推导和最右推导

L（G6）={aa*|a€{0，1，2，3，4，5，6，7，8，9}}

是 0~9 组成的数字串

0127

       最左推导：N=>ND     最右推导：N=>ND

                  =>NDD                             =>N7

                  =>NDDD                            =>ND7

                  =>DDDD                            =>N27

                  =>0DDD                             =>ND27

                  =>01DD                             =>N127

                  =>012D                             =>D127

                  =>0127                              =>0127

2.7 写一个文法，使其语言是奇数集，且每个奇数不以 0 开头

G[S]:S->ABC| C

         A->1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |9

         B->BE |ε

         E->0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |8 | 9  

         C->1 | 3 | 5 | 7 | 9 

2.8 令文法为    E->T|E+T|E-T
                     T->F|T*F|T/F
                     F->(E)|I
     (1) 给出 i+i *i 、 i*( i+i ) 的最左最右推导
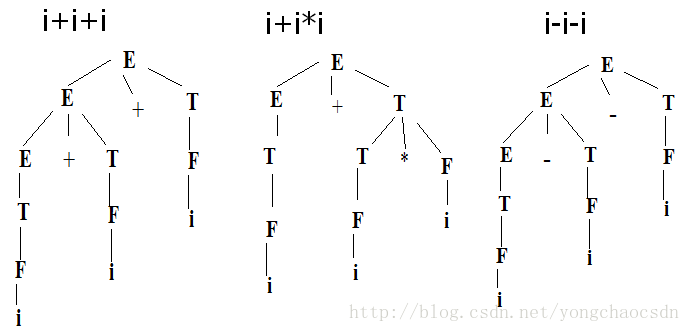
     (2) 给出 i+i+i 、 i+i *i 和 i-i-i 的语法树

1）i+i*i

   最左推导：E=>E+T             最右推导：E=>E+T

                      =>T+T                                =>E+T*F

                      =>F+T                                =>E+T*i

                      =>i+T                                =>E+F*i

                      =>i+T*F                             =>E+i*i

                      =>i+F*F                             =>T+i*i

                      =>i+i*F                             =>F+i*i

                      =>i+i*i                              =>i+i*i

  i*（i+i）

    最左推导：E=> T             最右推导：E=>T

                      => T*F                            => T*F

                      =>F*F                              =>T* ( E )

                      =>i*F                               =>T* ( E+T )

                      =>i* ( E )                          =>T* ( E+F )

                      =>i* ( E+T )                      =>T* (E+i )

                      =>i* ( T+T )                      =>T* (T+i )

                      =>i* ( F+T )                      =>T* (F+i )

                      =>i* ( i+T)                       =>T* ( i+i )

                      =>i* ( i +F )                      =>F* (i+i )

                      =>i* ( i+i)                        =>i* ( i+i )

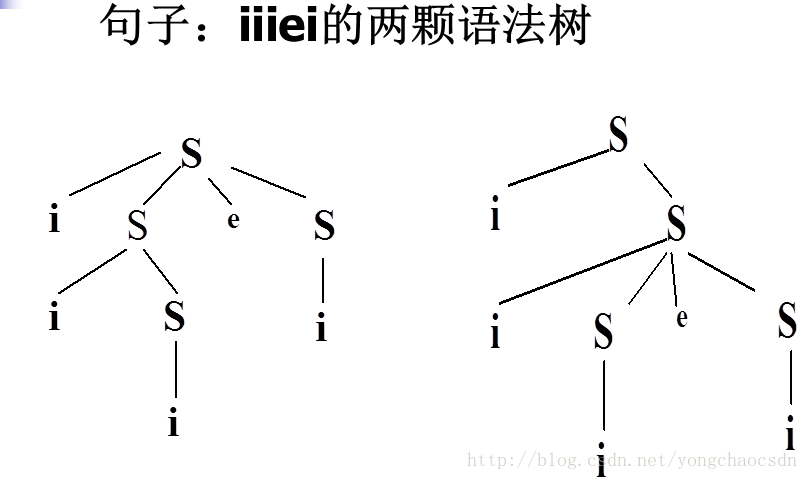
2.9证明下面的文法是二义的：
             S->iSeS|iS|i

2.11给出下面语言的相应文法

3.8给出下面正规表达式

以 01 结尾的二进制数串

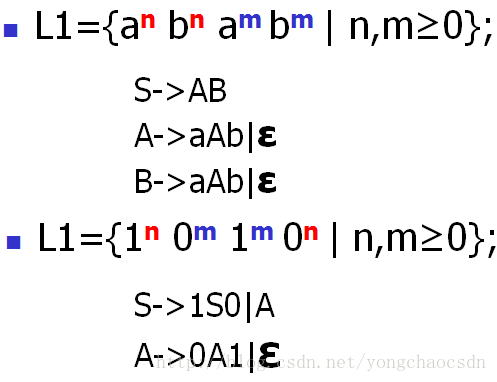
(0| 1)*01

能被 5 整除的十进制 整数

0| (+ | -)5 |

(+| -)(1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9)

(0| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9)*(0 | 5)

包含奇数个 1 或 奇数个 0 的二进制数串

1*0(1|01*0)*|0*1(0|10*1) *

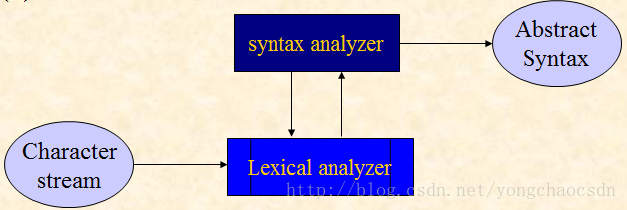
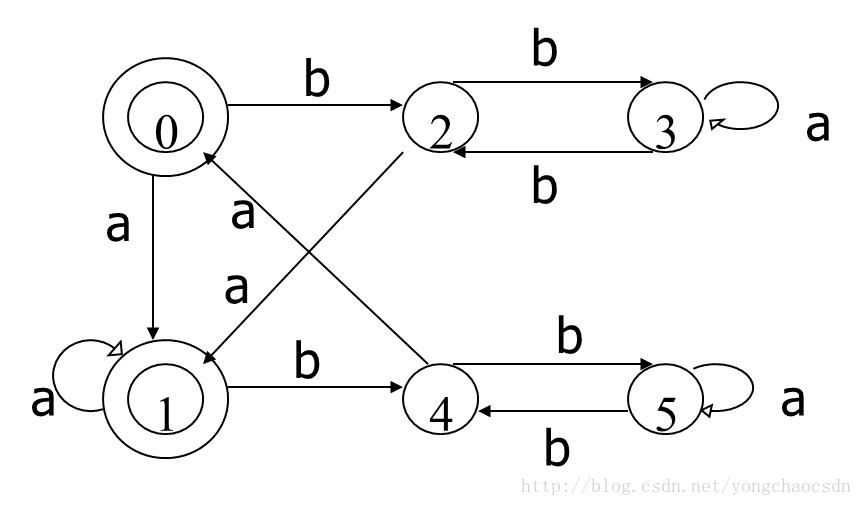
3.12将图3.18的（a）、（b）和（c）分别确定化和最少化。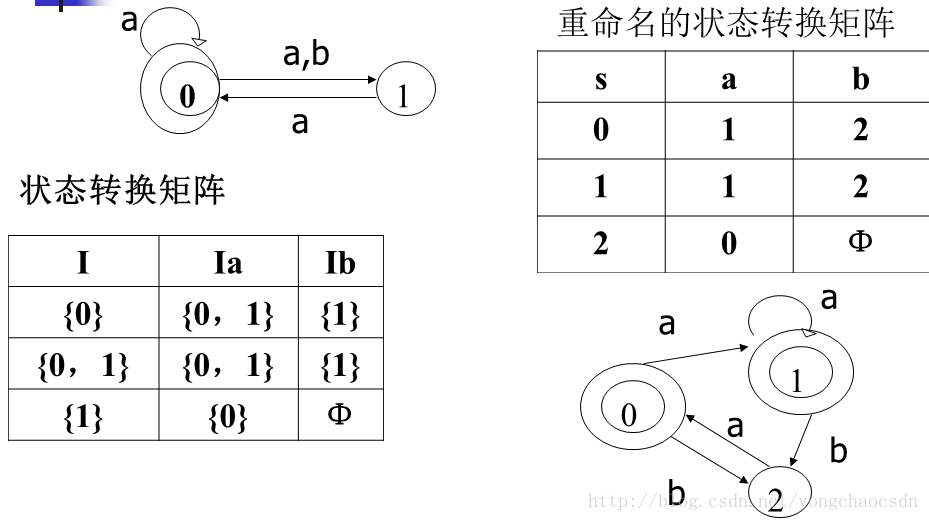

最小化Π{0，1}  {2}   {0，1}a={1}  {0，1}b={2}  所以0,1等价 

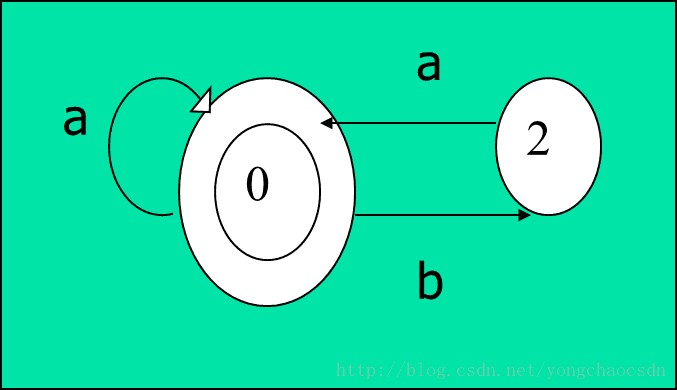
Π：{2，3，4，5}   {0，1}

{2，3，4，5}a={0，1，3，5}分属两区，

所以分为{2，4} {3，5}

{2，4}b={3，5}  2，4等价    

{3，5}b={2，4} 3，5等价

{0，1}a={1}      {0，1}b={2，4}   

 所以分为 {0，1}{2，4}{3，5}