机器学习实战第二课(PCA)

    PCA作为一种无监督的特征提取方法，在很多场合都能见到其应用，其主要功能是降低数据维度，减少数据冗余。关于PCA的理论知识这里不作太多讲解，大致流程：

(1)求数据的每一个维度的均值

(2)数据去均值处理

(3)构造协方差矩阵

(4)求特征值和特征向量

(5)取特征值较大的部分以及其对应的特征向量

(6)将原始数据映射到新的空间

具体实现：

import numpy as np
import matplotlib.pyplot as plt



def loadDataSet(fileName,delim = '\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [map(float,line) for line in stringArr]
    return np.mat(datArr)

def pca(dataMat,topNfeat = 9999999):
    
    #计算每一列的均值
    meanVals = np.mean(dataMat,axis = 0)
    
    #每个向量同时减去均值
    meanRemoved = dataMat - meanVals
    
    #构造协方差矩阵
    covMat = np.cov(meanRemoved,rowvar = 0)
    
    #求协方差的特征值和特征向量
    eigVals,eigVects = np.linalg.eig(np.mat(covMat))

    #对特征值进行排序，argsort返回的是从小到大的顺序
    eigValInd = np.argsort(eigVals)
    
    #-1表示倒序，返回topN的特征值[-1 到 -(topNfeat + 1)],但是不包括 -(topNfeat + 1)本身的倒序
    eigValInd = eigValInd[:-(topNfeat + 1) : -1]

    #重组 eigVects最大到最小
    redEigVects = eigVects[:,eigValInd]
    
    #将数据转换到新空间
    lowDataMat = meanRemoved * redEigVects
    
    #对降维后的数据进行重构
    reconMat = (lowDataMat * redEigVects.T) + meanVals
    
    return lowDataMat,reconMat


def replaceNanWithMean():
    dataMat = loadDataSet('secom.data',' ')
    numFeat = np.shape(dataMat)[1]
    
    for i in range(numFeat):
        #对value不为NaN的求均值
        #返回矩阵基于的数组
        meanVal = np.mean(dataMat[np.nonzero(~np.isnan(dataMat[:,i].A))[0],i])
        #将value为NaN的值赋值为均值
        dataMat[np.nonzero(np.isnan(dataMat[:,i].A))[0],i] = meanVal
    
    return dataMat
    


def analyse_data(dataMat):
    meanVals = np.mean(dataMat,axis = 0)
    meanRemoved = dataMat - meanVals
    covMat = np.cov(meanRemoved,rowvar = 0)
    eigvals,eigVects = np.linalg.eig(np.mat(covMat))
    eigValInd = np.argsort(eigvals)
    
    topNfeat = 20
    eigValInd = eigValInd[:-(topNfeat + 1):-1]
    cov_all_score = float(sum(eigvals))
    sum_cov_score = 0
    
    for i in range(0,len(eigValInd)):
        line_cov_score = float(eigvals[eigValInd[i]])
        sum_cov_score += line_cov_score
        
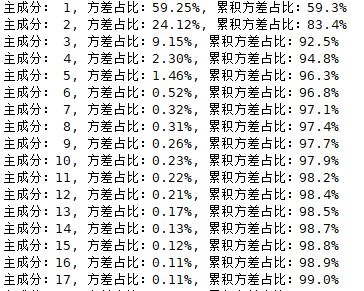
        print '主成分：%s, 方差占比：%s%%, 累积方差占比：%s%%' % (format(i+1, '2.0f'), format(line_cov_score/cov_all_score*100, '4.2f'), format(sum_cov_score/cov_all_score*100, '4.1f'))
        
        
if __name__ == "__main__":
    
    dataMat = replaceNanWithMean()
    print np.shape(dataMat)
    
    analyse_data(dataMat)

从实验看出，pca的前六个特征就占到了96.8%。