opencv 凸包convexHull、道格拉斯-普克算法Douglas-Peucker algorithm、approxPloyDP 函数

 

凸包convexHull、道格拉斯-普克算法Douglas-Peucker algorithm、approxPloyDP 函数

道格拉斯-普克算法（Douglas–Peucker algorithm），亦称为拉默-道格拉斯-普克算法（Ramer–Douglas–Peucker algorithm），这个算法最初由拉默（Urs Ramer）于1972年提出，1973年道格拉斯（David Douglas）和普克（Thomas Peucker）二人又独立于拉默提出了该算法。我们知道，一条曲线上包含着无数个点，但是计算机在存储曲线时只能存取有限个点，通常存储的点越多，那么对该曲线的描述也就越精确。当我们要对原本用N个点描述的曲线进行压缩表示时，即采用K（K<N）个点来描述曲线，为了尽可能保证原有曲线的形态不至有太大的改变，我们就需要一种算法，而道格拉斯-普克算法就是这样一种将曲线近似表示为一系列点，并减少点的数量的一种算法。它的优点是具有平移和旋转不变性，给定曲线与阈值后，抽样结果一定。

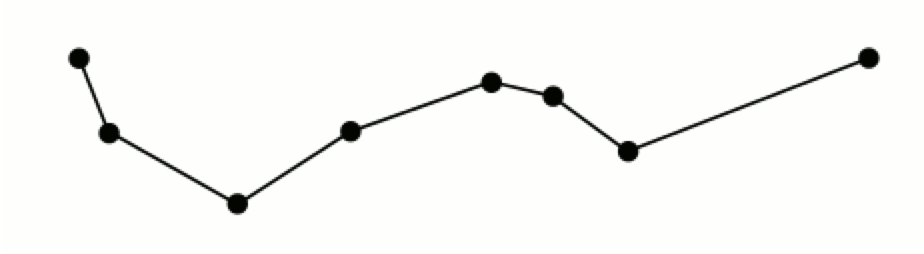
下面，我们通过一个例子来介绍一下该算法的执行步骤。假设当前我们有一条曲线，它由8各点来描述，如下图所示

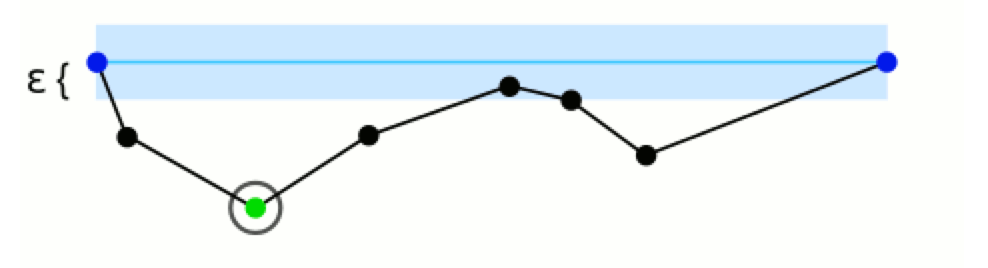
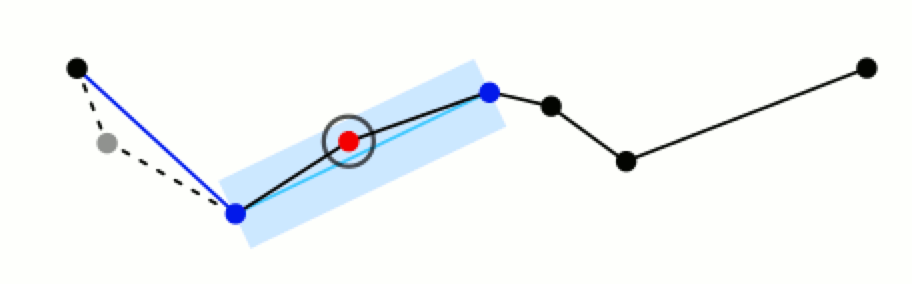
初始曲线是一系列有序的点集，我们需要设定一个距离（阈值）参数 ε > 0。最开始时，在曲线首尾两点A，B之间连接一条直线AB。算法自动将首尾两个点记下（也就是存入结果点集）。得到曲线上离该直线段（AB）距离最大的点C，计算其与AB的距离d，如下图所示

如果用直线段AB来作为原曲线的近似表示，那么点C显然是位于曲线上，离AB最远的点。现在比较距离 d 与预先给定的阈值 ε 的大小，如果小于 ε，则表明任何当前没有被记下的点都可以被丢弃了，因为用已经得到的直线段作为曲线的近似，不会比 ε 更早，即该段曲线处理完毕。

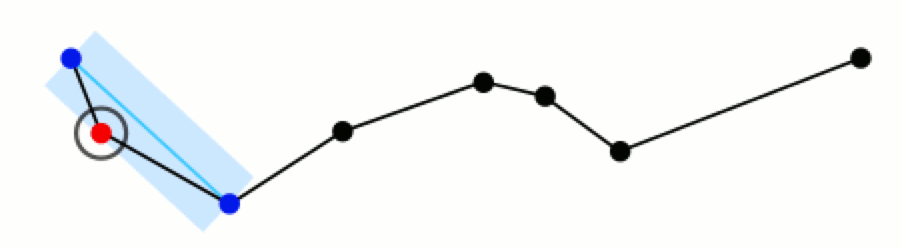
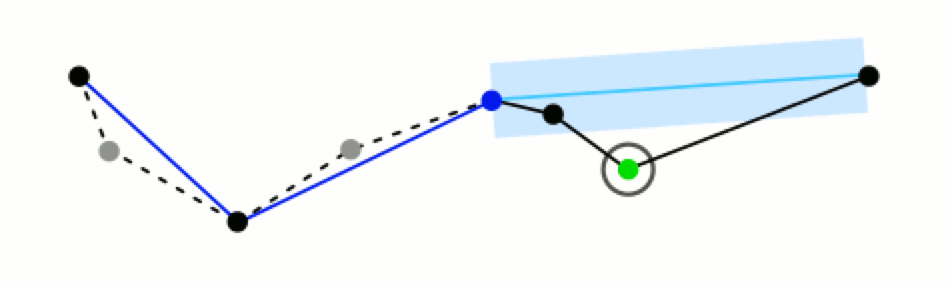
如果距离 d 大于阈值，则用C将曲线分为两段AC和BC，并将点C记下。

然后分别对已经得到两段曲线递归地进行上述处理。

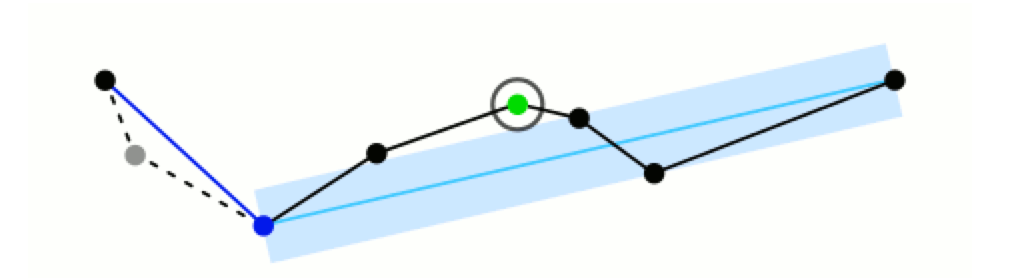
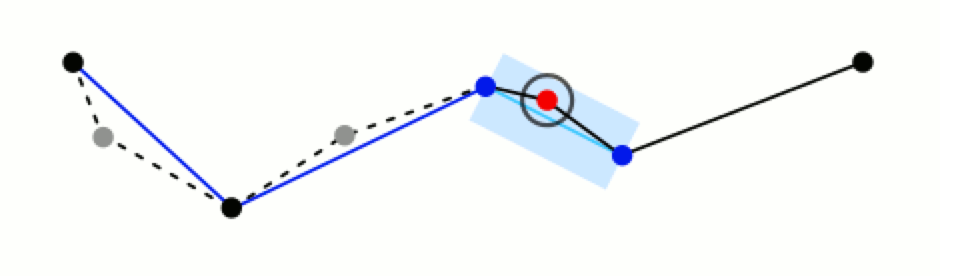
当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似。就本例而言，接下来的处理步骤如下图所示： 

                                    ↓   

                                    ↓

                                     ↓

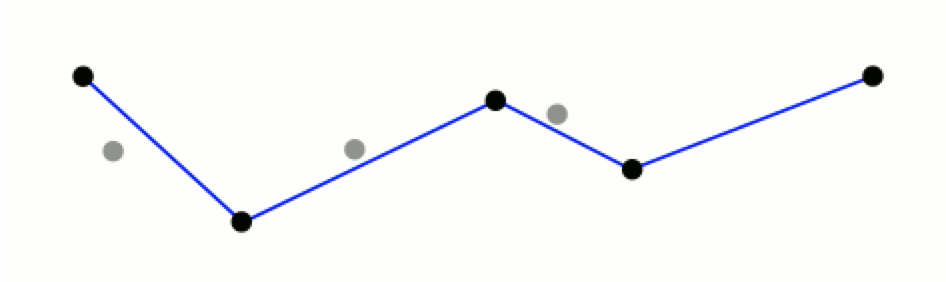
最终我们得到的（用更少的点表示的）近似曲线如下

参考：https://blog.csdn.net/baimafujinji/article/details/6475432

python 实现：

#-*- coding:utf-8 -*-
"""
道格拉斯算法的实现
程序需要安装shapely模块
"""
import math
from shapely import wkt,geometry
import matplotlib.pyplot as plt
 
class Point:
	"""点类"""
	x=0.0
	y=0.0
	index=0 #点在线上的索引
 
	def __init__(self,x,y,index):
		self.x=x
		self.y=y
		self.index=index
 
class Douglas:
	"""道格拉斯算法类"""
	points=[]
	D=1 #容差
 
	def readPoint(self):
		"""生成点要素"""
		g=wkt.loads("LINESTRING(1 4,2 3,4 2,6 6,7 7,8 6,9 5,10 10)")
		coords=g.coords
		for i in range(len(coords)):
			self.points.append(Point(coords[i][0],coords[i][1],i))
 
	def compress(self,p1,p2):
		"""具体的抽稀算法"""
		swichvalue=False
		#一般式直线方程系数 A*x+B*y+C=0,利用点斜式,分母可以省略约区
		#A=(p1.y-p2.y)/math.sqrt(math.pow(p1.y-p2.y,2)+math.pow(p1.x-p2.x,2))
		A=(p1.y-p2.y)
		#B=(p2.x-p1.x)/math.sqrt(math.pow(p1.y-p2.y,2)+math.pow(p1.x-p2.x,2))
		B=(p2.x-p1.x)
		#C=(p1.x*p2.y-p2.x*p1.y)/math.sqrt(math.pow(p1.y-p2.y,2)+math.pow(p1.x-p2.x,2))
		C=(p1.x*p2.y-p2.x*p1.y)
		
		m=self.points.index(p1)
		n=self.points.index(p2)
		distance=[]
		middle=None
 
		if(n==m+1):
			return
		#计算中间点到直线的距离
		for i in range(m+1,n):
			d=abs(A*self.points[i].x+B*self.points[i].y+C)/math.sqrt(math.pow(A,2)+math.pow(B,2))
			distance.append(d)
 
		dmax=max(distance)
 
		if dmax>self.D:
			swichvalue=True
		else:
			swichvalue=False
 
		if(not swichvalue):
			for i in range(m+1,n):
				del self.points[i]
		else:
			for i in range(m+1,n):
				if(abs(A*self.points[i].x+B*self.points[i].y+C)/math.sqrt(math.pow(A,2)+math.pow(B,2))==dmax):
					middle=self.points[i]
			self.compress(p1,middle)
			self.compress(middle,p2)
 
	def printPoint(self):
		"""打印数据点"""
		for p in self.points:
			print "%d,%f,%f"%(p.index,p.x,p.y)
 
def main():
	"""测试"""
	#p=Point(20,20,1)
	#print '%d,%d,%d'%(p.x,p.x,p.index)
	
	d=Douglas()
	d.readPoint()
	#d.printPoint()
	#结果图形的绘制，抽稀之前绘制
	fig=plt.figure()
	a1=fig.add_subplot(121)
	dx=[]
	dy=[]
	for i in range(len(d.points)):
		dx.append(d.points[i].x)
		dy.append(d.points[i].y)
	a1.plot(dx,dy,color='g',linestyle='-',marker='+')
 
	
	d.compress(d.points[0],d.points[len(d.points)-1])
 
	#抽稀之后绘制
	dx1=[]
	dy1=[]
	a2=fig.add_subplot(122)
	for p in d.points:
		dx1.append(p.x)
		dy1.append(p.y)
	a2.plot(dx1,dy1,color='r',linestyle='-',marker='+')
 
	#print "========================\n"
	#d.printPoint()
 
	plt.show()
 
if __name__=='__main__':
 
	main()

 

 

opencv多边形拟合曲线approxPolyDP()函数

approxPolyDP()函数是opencv中对指定的点集进行多边形逼近的函数，其逼近的精度可通过参数设置。

对应的函数为：
void approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed)；

例如：approxPolyDP(contourMat, approxCurve, 10, true);//找出轮廓的多边形拟合曲线

第一个参数 InputArray curve：输入的点集
第二个参数OutputArray approxCurve：输出的点集，当前点集是能最小包容指定点集的。画出来即是一个多边形。
第三个参数double epsilon：指定的精度，也即是原始曲线与近似曲线之间的最大距离。
第四个参数bool closed：若为true，则说明近似曲线是闭合的；反之，若为false，则断开。

该函数采用是道格拉斯-普克算法（Douglas-Peucker）来实现。该算法也以Douglas-Peucker算法和迭代终点拟合算法为名。是将曲线近似表示为一系列点，并减少点的数量的一种算法。该算法的原始类型分别由乌尔斯·拉默（Urs Ramer）于1972年以及大卫·道格拉斯（David Douglas）和托马斯·普克（Thomas Peucker）于1973年提出，并在之后的数十年中由其他学者予以完善。

经典的Douglas-Peucker算法描述如下：

（1）在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；

（2）得到曲线上离该直线段距离最大的点C，计算其与AB的距离d；

（3）比较该距离与预先给定的阈值threshold的大小，如果小于threshold，则该直线段作为曲线的近似，该段曲线处理完毕。

（4）如果距离大于阈值，则用C将曲线分为两段AC和BC，并分别对两段取信进行1~3的处理。

（5）当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似。
 

凸包convexHull

作用：找到2D点集的凸包

cv2.convexHull(points[, clockwise[, returnPoints]]]) -> hull

参数：

points - 2D点集 2D point set

clockwise - 布尔类型，默认false；若为true，输出的凸包则为顺时针方向；若为false，输出的凸包则为逆时针方向。注意：这里的坐标系是x轴方向指向右侧，y轴方向指向上方。

returnPoints - 布尔类型，默认true，在矩阵情况下，若为true，则返回凸包点集；若为false，则返回整数向量的索引

返回值：

hull - 输出的凸包，是整数向量的索引（an integer vector of indices）或点集向量（vector of points）

代码示例：

hull = cv2.convexHull(cnt)

运行效果：

 

代码综合

import cv2
import numpy as np

img = cv2.imread('Mjolnir.jpg')  
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)  
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)  
contours, hierarchy = cv2.findContours(binary,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE) 

for cnt in contours:

    # ----源轮廓-------
    cv2.drawContours(img, [cnt], -1, (0, 255, 0), 2)

    # 近似多边形
    # epsilon 为近似度参数，该值需要轮廓的周长信息
    # 多边形周长与源轮廓周长之比就是epsilon
    epsilon = 0.01 * cv2.arcLength(cnt,True)
    approx = cv2.approxPolyDP(cnt, epsilon, True)
    cv2.drawContours(img, [approx], -1, (255, 255, 0), 2)

    # 凸包
    hull = cv2.convexHull(cnt)
    cv2.drawContours(img, [hull], -1, (0, 0, 255), 2)

cv2.imshow("approx",img)
cv2.waitKey(0)
cv2.destroyAllWindows()

运行效果

 

参考：https://my.oschina.net/u/4320155/blog/3657674