Codeforces Round #813 (Div. 2)D. Empty Graph

   首先，我们先假设不进行任何操作，探究一下最短路径该怎么求。

        如何求最短路径？

        我们已知无法建图，就无法用相关算法。

1.我们尝试得到关于任意两点u，v的最短路径的公式

        我们默认u < v，并将d(u, v)定义为u到v的最短距离， 边(u, v)的权重为w(u, v)。

       

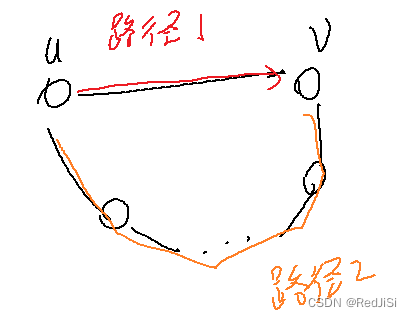
        根据最短路性质，我们知道d(u, v)  <= w(u, v) = min(au ~ av)。

        也就是说，如果d(u, v) < w(u, v)，那么说明d(u, v) 是 路径2 上的边权和

        而已知无法建图，我们需要用一些比较灵巧的贪心方式来求路径2的边权和。

        而我们知道路径2上的边数>=2的，那么不妨先讨论边数为2的情况。

        将mina = min(a1 ~ an)，而mini 为 a[i] = mina 的 索引i。

        那么，根据完全图的性质，我们知道u、v 和 mini 是 有边的。

        第一种情况：u < mini < v，那么则有d(u, v)  = d(u, mini) + d(mini, v) = 2mina

        第二种情况：mini  < u 或者 mini < v，那么则有d(u, v) = d(u, 1) + d(v, 1) = 2mina或者 d(u, n) + d(v, n) = 2 * mina;

        显然，边数 > 2 的情况无法优于我们构建的。

        那么，我们可以证出：任意两点的最短路的公式：

        任意u, v，则有 d(u, v) = min(min(au ~ av), 2 * mina)。（mina = min(a1 ~ an))。

2.我们尝试求出k = 0时题目的答案。（题目本身要求k = 1 ~ n）

        我们已知任意两点u, v的最短路径为d(u, v) = min(min(au ~ av), 2 * mina)。

        而我们要求的是n个点 中 选两点间最短路径的最大值dmax，如果直接枚举的话是n（n - 1）次，这样的时间复杂度是无法接受的。

        但是我们真的需要枚举那么多吗？

        那么，如果2 * mina 为常数，我们重点关注的是min(au ~ av)。

        而如果有dmax != 2 * mina，反而 等于 a[i]。

        那么，我们已知d(i, i + 1) = d(i, i + 2) = …… = d(i, n) = a[i]，则我们只需枚举min(a[i], a[i + 1])即可。这样的话我们就可以把枚举的时间复杂度降到On

3.我们尝试进行k次操作

     很容易证明，选择ai = x（x <= 1e9），其中x = 1e9 最优。

     而我们想要让dmax = max(min(a[i] , a[i + 1]), mina)变大。

     如果k == n，那么我将所有的a[i] 都变为1e9即可。

      而如果k != n，那么我们需要考虑，dmax想要变大只能通过两种途径，一是min(a[i], a[i + 1])，二是mina。

        而我们假设dmax 最终 = max(min(a[i], a[i + 1]))，由于我们无法让所有的a[i]都等于1e9，那么我们只需要让min(maxa, a[i])中的a[i]变为1e9即可，而如此我们操作1次即可，而剩下的还有k - 1次。

        但同时d(u, v) = min(maxa, 2 * mina)。我们知道，要想让dmax = maxa，首先要让d(u, v) = maxa，那么我们就要用剩下的k - 1 次尽可能抬高2 * mina。

        而我们假设dmax 最终 = max(mina)，那么我们让最小的k个a[i] = 1e9即可。

 而我们知道，如果和maxa相邻的正好在k 个 最小的a里的话，那么其实上两种假设在操作层面是一样的。

        而如果不在的话，那么我们就用k - 1 次操作后的mina * 2 去和 maxa做个比较即可。

4.实现细节

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define y second
#define x first
typedef pair<int,int> PII;
typedef long long LL;
typedef unsigned long long ULL;
const int mod = 1e9 + 7;
const int N = 3e5 + 10, M = 2 * N, P =  131;

int n, k;
int a[N];
PII v[N];

void solve()
{
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) cin >> a[i], v[i] = {a[i], i};


	sort(v + 1, v + 1 + n);

	for(int i = 1; i <= k - 1; i ++)
	{
		v[i].x = 1e9; a[v[i].y] = 1e9;
	}

	sort(v + 1, v + 1 + n);
	
	int ans1 = min(v[1].x * 2, v[n].x);
	v[1].x = 1e9, a[v[1].y] = 1e9;
	sort(v + 1, v + 1 + n);
	
	int ans2 = -1;
	for(int i = 1; i <= n - 1; i ++)
		ans2 = max(ans2, min(a[i], a[i + 1]));
		
	ans2 = min(v[1].x * 2, ans2);
	
	cout << max(ans1, ans2) << endl;
}

int main(){
std::ios::sync_with_stdio(false);std::cin.tie(0);
int T; cin >> T; while(T -- ){solve();}}