三、递归树分析法

最新推荐文章于 2023-06-15 10:27:20 发布

FibonacciCode

最新推荐文章于 2023-06-15 10:27:20 发布

阅读量1k

点赞数

分类专栏：算法导论

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/yuebowhu/article/details/111995489

版权

本文探讨了使用递归树和归纳法来分析算法的时间复杂度。通过递归树分析，得出算法的上界，再用归纳法证明这个上界同样为下界。具体分为三种情况讨论，展示了从非严谨分析到严谨证明的过程，并强调了这种方法在处理不符合主定理情形时的价值。递归树和归纳法结合的证明策略在算法分析中具有重要意义。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1 问题

在这里插入图片描述

2 解决思路

使用递归树猜想一个上界，使用归纳法证明上界也是下界。

2.1 使用递归树（recursion tree）猜想结论（不严谨）

使用递归树两点：1⃣️逐行展开；2⃣️逐行相加；

逐行展开

本质上是分解问题，每个非叶子结点表示分解+合并问题所付出的代价，叶子结点表示解决边界问题所付出的代价。
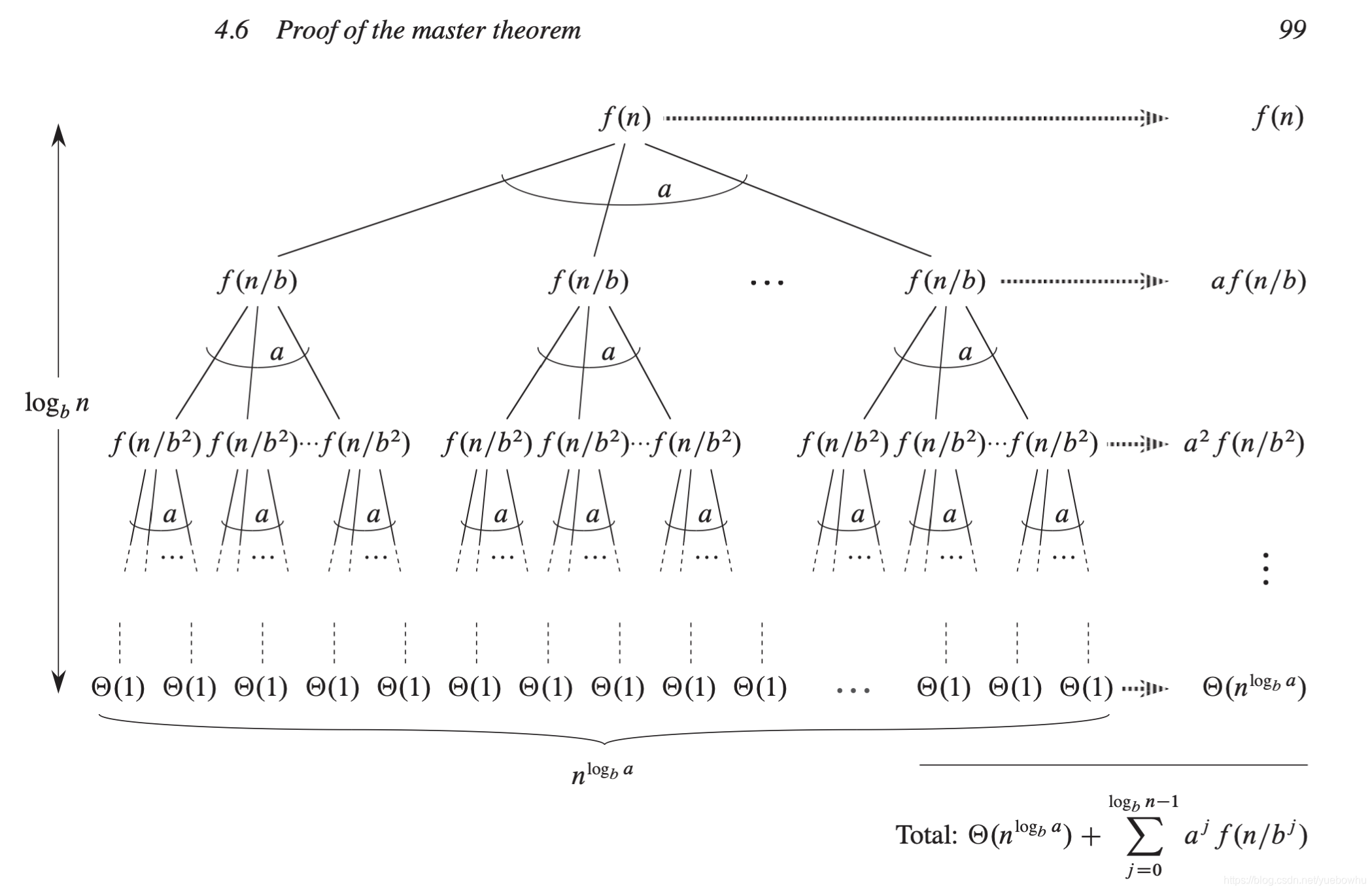
在这里插入图片描述

逐层求和

这里要注意，除去非叶子结点，每一层的和呈现出等比数列性质，计算整个代价 $T (n)$ 本质上就是分解（合并）问题付出的代价+解决递归边界付出的代价。

Case1:

分解问题的代价：
在这里插入图片描述

解决递归边界的代价：
$\Theta(n^{log_ba})$

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。