这几天在做短文本主题发现时,考虑使用聚类算法不同一主题的文本聚集到一块,因此读了这篇论文:
A Dirichlet Multinomial Mixture Model-based Approach for Short Text Clustering
在该文中,作者使用“a collapsed Gibbs Sampling algorithm for the Dirichlet Multinomial Mixture model (GSDMM)”来进行短文本聚类。
GSDMM的优点包括:
1. 可以在完备性和一致性之间平衡,自动得到一个较优的聚类个数;
2. 可以处理稀疏的、高维度的短文本,并能得到每一个簇的代表词;
3. 实验表明比其他的聚类算法性能更好。
首先,聚类问题主要需要解决的问题包括:
1. 设置簇的个数,即需要聚几个类;
2. 处理高维数据;
3. 结果的可读性(可解释性);
4. 对于处理大规模数据的能力。
在该文中,作者为了解决以上问题,提出了GSDMM方法,并使用了电影分组过程(Movie Group Process, MGP)来进行类比说明。
文本聚类和电影分组过程的对应关系为:
文档D <----> 学生总数
每篇文档 <----> 每个学生
文档包括的单词 <----> 学生看过的电影
然后短文本聚类问题就可以看作:把学生分组,然后每一组的学生看的电影的类型都一致,不同组的学生的观影兴趣不同。
下面介绍一下电影分组过程:
首先预定义K个组,然后随机把学生分派到这K个组中,接下来让每个学生重新选择分组。学生选择分组基于以下两条准则:
Rule 1: 选择学生更多的组;
Rule 2: 选择跟自己兴趣相近的组;
随着这一过程的进行,一些组会变大,同时有些组会消失,最终得到的结果是只有原来K个组的一部分得以保留,并且每一组的学生的观影兴趣相同。
以上过程的两个规则和聚类的两个任务相同:
Rule 1趋向于让簇的完备性更强,即同一个簇中尽量多的包含属于该类的文本(学生);
Rule 2趋向于让簇的一致性更强,即尽可能让有着同一兴趣的学生在一个簇中。
以上过程和GSDMM等价,接下来介绍理论部分,首先是狄利克雷多项式混合模型:
Dirichlet Multinominal Mixture (DMM):
DMM是文档的概率产生式模型,它包括产生式过程的两个假设:
1. 文档是根据一个混合模型产生的;
2. 混合模型组件和簇之间有一一对应的关系;(There is a one-to-one correspondence between mixture components and clusters)
在产生文档d的过程中,DMM首先根据混合权重(簇的权重)p(z = k)来选择一个组件(簇)k,然后根据每个文档在簇中的权重p(d | z = k)选择一个文档。
该过程可以描述为:
其中,K是所有的簇数(混合组件)
为了得到P(d | z = k)和p(z = k), DMM做了朴素贝叶斯假设:当一个文档所属的类已知时,该文档中的所有单词独立分布,并且单词和它在文档中的位置是独立分布的。
根据该假设,由簇k得到的文档d的概率是:
Nigam等在论文中假设簇在单词上是多项式分布:
对于每个簇来说,狄利克雷分布是其先验分布:
并且每个簇的权重是从一个多项式分布中采集的:
其中k = 1, ……, K,
并假设了该多项分布的狄利克雷先验:
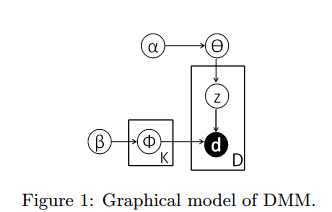
该DMM的图模型如下所示:
对于每篇文档来说,我们要估计的是它所属于的簇,这里使用GSDMM方法。
GSDMM
该算法跟上文提及的电影分组过程是相同的。
首先介绍一下算法要用的一些变量,如表1所示:
如Algorithm 1所示:
如表1所示,在Algorithm 1 中,文档为
首先初始化每个簇的元素,包括该簇的文档数,该簇中所含的单词数,该簇中单词w出现的次数,将它们都设置为0,
然后对于每一个文档d,执行:
根据簇的多项式分布给该文档分配簇标签;
然后相应的参数都进行改变:包括该簇文档数 = 该簇的原文档数 + 1,该簇单词数 = 该簇的原单词数 + 文档d所含的单词数,该簇每个单词出现个数 = 该簇中相应的单词出现个数 + 该单词在文档d中出现个数;
对每一个文档初始化完成后,我们得到了K个簇,并且每个文档d属于且只属于一个簇;
然后执行迭代算法:
在每一层迭代里执行以下过程:
对于每一个文档d:
记录d所属的簇,
然后从该簇中去除d的信息,包括:该簇文档数 = 该簇的原文档数 - 1,该簇单词数 = 该簇的原单词数 - 文档d所含的单词数,该簇每个单词出现个数 = 该簇中相应的单词出现个数 - 该单词在文档d中出现个数;
然后根据等式
将文档d分配给该簇后,更新改簇信息,包括:包括该簇文档数 = 该簇的原文档数 + 1,该簇单词数 = 该簇的原单词数 + 文档d所含的单词数,该簇每个单词出现个数 = 该簇中相应的单词出现个数 + 该单词在文档d中出现个数;
可以看出,Algorithm 1中的核心部分是两个步骤,
1. 初始化时给每个文档分配簇:
2. 迭代算法中给每个文档重新分配簇:
接下来我们主要解释第二个分布。
从图1中可以得到:
而
其中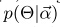
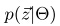
根据近似算法,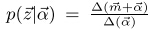
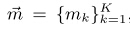
而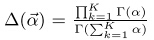
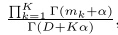
D为所有的文档个数,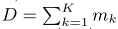
同理,
其中,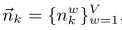
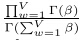
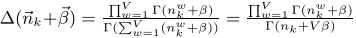
因此,联合概率等价于:









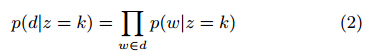
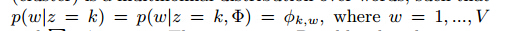

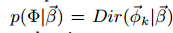
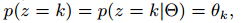
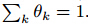
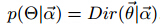





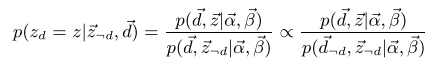
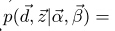
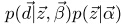
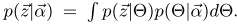
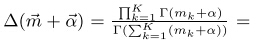
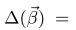
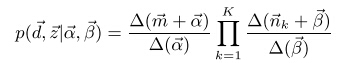
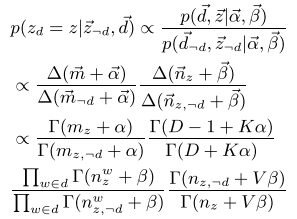

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








