小波

摘自：http://zh.wikipedia.org/wiki/%E5%B0%8F%E6%B3%A2%E5%88%86%E6%9E%90

定义：wavelet是指小型波(在傅里叶分析里的弦波是大型波)，简单说来，小波(wavelet)是一个衰减迅速的振荡。

小波函数：小波只有时域表示，作为小波函数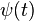。例如墨西哥帽小波。

     

小波历史：
1909年: 第一个小波（Haar小波）由Alfred Haar提出
1981年: Jean Morlet提出小波概念
1984年: Morlet和 Grossman发明了"wavelet"一词
1985年: Meyer小波
1987年: 第一届国际研讨会在法国
1988年: Stephane Mallat和 Meyer 提出了多清晰度的概念
1988年: 多贝西小波
1989年: 快速小波转换 （FWT）
1990年代: 离散小波变换 （DWT）
1999年: 方向小波转换
2000年: JPEG2000

小波转换的优点：

1. 可以同时观察频率和时间轴，在频率高时有较好的时间清晰度，在频率低时有较好的频率清晰度。
2. 有快速小波转换可以加速运算。
3. 可以分离出信号的精细或粗糙成分。
4. 在小波理论中，可以用较少的小波系数去逼近一个函数。
5. 对信号去噪或压缩信号时，不会对信号造成明显的破坏。

小波变换的实质: 

小波变换的公式有内积形式和卷积形式，两种形式的实质都是一样的．它要求的就是一个个小波分量的系数也就是＂权＂．其直观意义就是首先用一个时窗最窄，频窗最宽的小波作为尺子去一步步地＂量＂信号，也就是去比较信号与小波的相似程度．信号局部与小波越相似，则小波变换的值越大，否则越小！当一步比较完成后，再将尺子拉长一倍，又去一步步地比较，从而得出一组组数据．如此这般循环，最后得出的就是信号的小波分解（小波级数）．当然这只是一种粗略的解释．