二叉搜索树应用分析

二叉搜索树（B树）

特性

1.所有非叶子结点至多拥有两个儿子（Left和Right）；

2.所有结点存储一个关键字；

3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

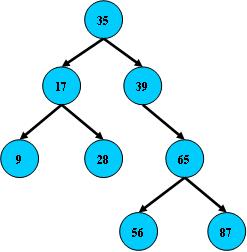
基本操作

1. 搜索

    struct TreeNode {
        int val;
        TreeNode * left;
        TreeNode * right;
        TreeNode(int val1): val(val1),left(nullptr),right(nullptr){}
    };
    TreeNode * search(TreeNode * root, int key) {
        if(root == nullptr)
            return nullptr;
        if(root ->val == key)
            return root;
        if(root ->val > key)
            return search(root ->left, key);
        else
            return search(root ->right, key);
    }

这个过程是根据B树自身性质决定的，搜索一个关键字，有以下几种情况：

1. 当前的节点会是nullptr，说明没有合适的节点，返回空指针
2. 找到，返回当前节点的指针

3. 当前节点的值大于目标值，根据B树定义，目标值可能存在于当前节点的左子树中；对于当前节点的值小于目标值，根据B树定义，目标值可能存在于当前节点的右子树种

   时间、空间复杂度分析
   时间复杂度O（lgn），这个和树高有关，极端情况下为O（n），一般会采用BST，平衡二叉搜索树。空间复杂度O（1）

2.插入

    void insert(TreeNode * root, int val) {
        if(search(root,val) != nullptr)
            return;
        TreeNode * p = root;
        Treenode * father = nullptr;
        while(p != nullptr) {
            father = p;
            if(p ->val > val)
                p = p ->left;
            else
                p = p ->right;
        }
        p = new TreeNode(val);
        if(father ->val > val)
            father ->left = p;
        else
            father ->right = p;
    }

首先，使用search，如果在B树中找到与之一致的节点，那么放弃插入。如没有找到，那么模拟查找的过程，找到需要插入的父节点，插入。

时间、空间复杂度分析
这里时间复杂度还是根据平均情况（BST）分析，O（lgn），空间复杂度O（1）

1. 删除

 TreeNode * delete(TreeNode * root, int val) {
        if(search(root,val) == nullptr)
            return;
        if(root ->val == val) {
            if(root ->left == nullptr && root ->right == nullptr) {
                delete root;
                return nullptr;
            }
            else if(root ->left == nullptr) {
                TreeNode * p = root ->right;
                delete root;
                return p;
            }
            else if(root ->right == nullptr) {
                TreeNode * p = root ->left;
                delete root;
                return p;
            }
            else {
                TreeNode * q = root ->left;
                TreeNode * qFather = nullptr;
                while(q ->right != nullptr) {
                    qFather = q;
                    q = q ->right;
                }
                root ->val = q ->val;
                if(qFather ->left == q) {
                    qFather ->left = nullptr;
                    delete q;
                }
                else {
                    qFather ->right = nullptr;
                    delete q;
                }
            }

        }
        TreeNode * p = root;
        Treenode * father = nullptr;
        while(p != nullptr) {
            father = p;
            if(p ->val > val)
                p = p ->left;
            else
                p = p ->right;
        }
        if(p ->left == nullptr && p ->right == nullptr) {
            if(father ->val > val)
                father ->left = nullptr;
            else
                father ->right = nullptr;
            delete p;
        }
        else if(p ->left == nullptr) {
            if(father ->val > val)
                father ->left = p ->right;
            else
                father ->right = p ->right; 
            delete p;       
        }
        else if(p ->right == nullptr) {
            if(father ->val > val)
                father ->left = p ->left;
            else
                father ->right = p ->left;
            delete p;           
        }
        else {
            TreeNode * q = p ->left;
            TreeNode * qFather = p;
            while(q ->right != nullptr) {
                qFather = q;
                q = q ->right;          
            }
            p ->val = q->val;
            delete q;
            if(p == qFather)
                p ->left = nullptr;
            else
                qFather ->right = nullptr;              
        }   
    return root;        
 }

首先使用search，假设当前节点不在B树内，返回。在B树内，会分成两种情况：

1. 删除的是根节点，分成三种情况：

   1. 左右子树均为空，返回空指针
   2. 左右子树有一个不为空，返回非空的子树
   3. 左右子树均不为空，这种比较麻烦一点，需要找到需要删除节点的前驱或者后继节点，我在代码里使用的是前驱，用前驱节点代替要删除节点，删除前驱节点原位置那个点

2. 删除的不是根节点
   找到要删除的节点的父节点，又分成三种情况：

   1. 要删除节点左右子树均为空，那么直接删除即可
   2. 要删除节点左右子树只有一个不为空，直接用非空子树的根代替要删除的节点即可
   3. 要删除的节点左右子树均不为空，这种比较麻烦一点，需要找到需要删除节点的前驱或者后继节点，我在代码里使用的是前驱，用前驱节点代替要删除节点，删除前驱节点原位置那个点
      注意：记得delete不用的空间

时间、空间复杂度分析
时间复杂度O（lgn），同样也是与树高有关，空间复杂度O(1)

后续会持续更新hash、B-，B+树的内容，如果发现文章内有错误，还望各位指正，谢谢。