今天给大家介绍一下区间调度问题。区间调度是一类难度比较大,但同时应用比较广的问题,经常会在面试中以各种形式出现。本文将会介绍区间调度的各种变形,希望能使大家在面临区间调度问题时得心应手,并可以在实际工作中巧妙应用。
###1. 相关定义
在数学里,区间通常是指这样的一类实数集合:如果x和y是两个在集合里的数,那么,任何x和y之间的数也属于该集合。区间有开闭之分,例如(1,2)和[1,2]的表示范围不同,后者包含整数1和2。
在程序世界,区间的概念和数学里没有区别,但是往往有具体的含义,例如时间区间,工资区间或者音乐中音符的开始结束区间等,图一给出了一个时间区间的例子。区间有了具体的含义之后,开闭的概念就显得非常重要,例如时间区间[8:30,9:30]和[9:30,10:30]两个区间是有重叠的,但是[8:30,9:30)和[9:30,10:30)没有重叠。在不同的问题中,区间的开闭往往不同,有时是闭区间,有时是半开半闭区间。时间区间往往是闭区间,但是音符中的开始结束区间则是半开半闭区间,所以在重叠的定义上大家需要具体问题具体分析。稍后你会发现,开闭的区别其实只是差一个等号而已。

//用于对工作排序的pair数组
pair<int,int> itv[MAX_N];
void solve()
{
//对pair进行的是字典序比较,为了让结束时间早的工作排在前面,把T存入first,//把S存入second
for(int i=0;i<N;i++)
{
itv[i].first=T[i];
itv[i].second=S[i];
}
sort(itv,itv+N);
//t是最后所选工作的结束时间
int ans=0,t=0;
for(int i=0;i<N;i++)
{
if(t<itv[i].second)//判断区间是否重叠
{
ans++;
t=itv[i].first;
}
}
printf(“%d\n”,ans);
}
时间复杂度:排序 $O(nlogn)$ +扫描$O(n) = O(nlogn) $。该问题已给出最优解,也即用贪心法可以解决。但是思考的思路如何得来呢?我们一步步分析,看看能不能最终得到和贪心法一样的结果。
最优化问题都可以通过某种搜索获得最优解,最多区间调度问题也不例外。该问题无非就是选择几个不重叠的区间而已,看看最多能选择多少个,其解空间为一棵二叉子集树,某个区间选或者不选构成了两个分支,如图四所示。我们的目标就是遍历这棵子集树,然后看从根节点到叶节点的不重叠区间的最大个数为多少。可以看出,该问题的解就是n位二进制的某个0/1组合。子集树共有2n种组合,每种组合都需要判断是否存在重叠区间,如果不重叠则获得1的个数。

<div align = center>图4 区间调度的子集树</div>
假设我们不对区间进行排序,则每种组合判断是否有重叠区间的复杂度为$O(n^2)$,从而整个算法复杂度为$O(2^n n^2)$。复杂度相当高!进行各种剪枝也无济于事!下面我们开始对算法进行优化。
让我们感到奇怪的是,只是判断n个区间是否存在重叠最坏居然也需要$O(n^2)$的复杂度。这是因为在区间无序的情况下,每个区间都要顺次和后面的所有区间进行比较,没有合理利用区间的两个时间点。我们考虑对区间进行一下排序会有什么不同。假设我们按照开始时间进行排序,排序之后有$\small x_{i-1}\leqslant x_{i}\leqslant x_{i+1}$,然后从第一个区间开始判断。第一个区间只需要和第二个区间进行判断即可。如果重叠,则这n个区间存在重叠,后面无需再进行判断;如果不重叠,我们只需要再将第二个和第三个进行同样的判断即可。所以按照开始时间进行排序之后,判断n个区间是否存在重叠的复杂度将为$O(n)$,所以整个算法复杂度降为$O(n2^n)$。按照结束时间进行排序也会有同样的结论。
虽然排序可以降低复杂度,但是遍历子集树的代价还是太大。我们换个角度考虑问题,看能不能避免遍历子集树。突破点在哪呢?我们不妨从第一个区间是否属于最优解开始。首先假设区间按照开始时间排序,并且已经求出最优解对应的所有区间。如果最优解中开始时间最小的区间$\small I_{1}^{'}$不是所有区间中开始时间最小的区间$\small I_{1}$,我们看看能否进行替换。$\small I_{1}$和$\small I_{1}^{'}$肯定是重叠的,否则就可以将$\small I_{1}$添加到最优解中获得更好的最优解。能否将$\small I_{1}^{'}$替换成$\small I_{1}$呢?$\small I_{1}$和$\small I_{1}^{'}$满足$\small s_{1}\leqslant s_{1}^{'}$,但是结束时间不确定,这就可能出现$\small e_{1}\geqslant e_{1}^{'}$的情况,从而也会出现$\small e_{1}\geqslant e_{i}^{'}(i>1)$的情况,从而替换可能会引入重叠,最优解变成非最优解。所以在按照开始时间排序的情况下,第一个区间不一定属于最优解。
我们再考虑一下按照结束时间排序的情况,也已经求出最优解对应的所有区间。如果最优解中结束时间最小的区间$\small I_{1}^{'}$不是所有区间中结束时间最小的区间$\small I_{1}$,我们看看能否进行替换。$\small I_{1}$和$\small I_{1}^{'}$肯定是重叠的,否则就可以将$\small I_{1}$添加到最优解中获得更好的最优解。能否将$\small I_{1}^{'}$替换成$\small I_{1}$呢?$\small I_{1}$和$\small I_{1}^{'}$满足$\small e_{1}\leqslant e_{1}^{'}$,$\small I_{1}^{'}$和$\small I_{2}^{'}$满足$\small e_{1}^{'}\leqslant s_{2}^{'}$(两个区间不重叠),所以有$\small e_{1}\leqslant s_{2}^{'}$,从而$\small I_{1}$和$\small I_{2}^{'}$不重叠。所以我们可以用$\small I_{1}$来替换$\small I_{1}^{'}$。这就得出一个结论:在按照结束时间排序的情况下,第一个区间必定属于最优解。按照这个思路继续推导剩下的区间我们就会发现:每次选结束时间最早的区间就可以获得最优解。这就和我们一开始给出的结论一致。
经过上面的分析,我们就明白为啥选择结束时间最早的工作就可以获得最优解。虽然我们并没有遍历子集树,但是它为我们思考和优化问题给出了一个很好的模型,希望大家能好好掌握这种构造问题解空间的方法。
下面我们再换个角度考虑上面的问题。很多最优化深搜问题都可以巧妙地转化成动态规划问题,可以转化的根本原因在于存在重复子问题,我们看图四就会发现最多区间调度问题也存在重复子问题,所以可以利用动态规划来解决。假设区间已经排序,可以尝试这样设计递归式:前i个区间的最多不重叠区间个数为dp[i]。dp[i]等于啥呢?我们需要根据第i个区间是否选择这两种情况来考虑。如果我们选择第i个区间,它可能和前面的区间重叠,我们需要找到不重叠的位置k,然后计算最多不重叠区间个数dp[k]+1(如果区间按照开始时间排序,则前i+1个区间没有明确的分界线,我们必须按照结束时间排序);如果我们不选择第i个区间,我们需要从前i-1个结果中选择一个最大的dp[j];最后选择dp[k]+1和dp[j]中较大的。伪代码如下:
void solve()
{
//1. 对所有的区间进行排序
sort_all_intervals();
//2. 按照动态规划求最优解
dp[0]=1;
for (int i = 1; i < intervals.size(); i++)
{
//1. 选择第i个区间
k=find_nonoverlap_pos();
if(k>=0) dp[i]=dp[k]+1;
//2. 不选择第i个区间
dp[i]=max{dp[i],dp[j]};
}
}
选择或者不选择第i个区间都需要去查找其他的区间,顺序查找的复杂度为$O(n)$,总共有n个区间,每个区间都需要查找,所以动态规划部分最初的算法复杂度为$O(n^2)$,已经从指数级降到多项式级,但是经过后面的优化还可以降到$O(n)$,我们一步步来优化。
**可以看出dp[i]是非递减的**,这可以通过数学归纳法证明。也即当我们已经求得前i个区间的最多不重叠区间个数之后,再求第i+1个区间时,我们完全可以不选择第i+1个区间,从而使得前i+1个区间的结果和前i个区间的结果相同;或者我们选择第i+1个区间,在不重叠的情况下有可能获得更优的结果。dp[i]是非递减的对我们有什么意义呢?首先,如果我们在计算dp[i]时不选择第i个区间,则我们就无需遍历前i-1个区间,直接选择dp[i-1]即可,因为它是前i-1个结果中最大的(虽然不一定是唯一的),此时伪代码中的dp[j]就变成了dp[i-1]。其次,在寻找和第i个区间不重叠的区间时,我们可以避免顺序遍历。如果我们将dp[i]的值列出来,肯定是这样的:
1,1,…,1,2,2,…,2,3,3,…,3,4……
即dp[i]的值从1开始,顺次递增,每一个值的个数不固定。dp[0]肯定等于1,后面几个区间如果和第0个区间重叠,则的dp值也为1;当出现一个区间不和第0个区间重叠时,其dp值变为2,依次类推。由此我们可以得到一个快速获得不重叠位置的方法:重新开辟一个新的数组,用来保存每一个不同dp值的最开始位置,例如pos[1]=0,pos[2]=3,…。这样我们就可以利用$O(1)$的时间实现find_nonoverlap_pos函数了,然后整个动态规划算法的复杂度就降为$O(n)$了。
其实从dp的值我们已经就可以发现一些端倪了:**dp值发生变化的位置恰是出现不重叠的位置**!再仔细思考一下就会出现一开始提到的贪心算法了。所以可以说,贪心算法是动态规划算法在某些问题中的一个特例。该问题的特殊性在于只考虑区间的个数,也即每次都是加1的操作,后面会看到,如果变成考虑区间的长度,则贪心算法不再适用。
####3.2 最大区间调度
该问题和上面最多区间调度问题的区别是不考虑区间个数,而是将区间的长度和作为一个指标,然后求长度和的最大值。我们将该问题命名为最大区间调度问题。
WAP某年的笔试题就考察了该问题([下载](http://download.csdn.net/download/yutianzuijin/8607053))。看这样一个例子:现在有n个工作要完成,每项工作分别在 时间开始,在 时间结束。对于每项工作,你都可以选择参与与否。如果选择了参与,那么自始至终都必须全程参与。此外,参与工作的时间段不能重叠(闭区间)。求你参与的所有工作最大需要耗费多少时间。
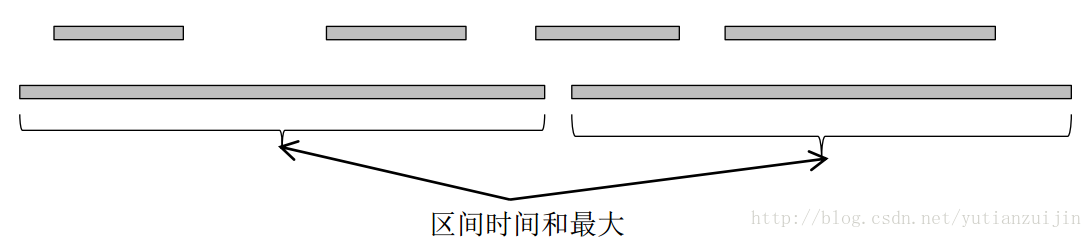
<div align = center>图5 最大区间调度</div>
该问题和最多区间调度很相似,一个考虑区间个数的最大值,一个考虑区间长度的最大值,但是该问题的难度要比最多区间调度大些,因为它必须要用动态规划来高效解决。在最多区间调度问题中,我们用动态规划的方法给大家解释了贪心算法可以解决问题的缘由,而最大区间调度问题则是直接利用上面提到的动态规划算法:首先按照结束时间排序区间,然后按照第i个区间选择与否进行动态规划。我们先给出WAP笔试题的核心代码:
public int getMaxWorkingTime(List intervals) {
/*
* 1 check the parameter validity
*/
/*
* 2 sort the jobs(intervals) based on the end time
*/
Collections.sort(intervals, new EndTimeComparator());
/*
* 3 calculate dp[i] using dp
*/
int[] dp = new int[intervals.size()];
dp[0] = intervals.get(0).getIntervalMinute();
for (int i = 1; i < intervals.size(); i++) {
int max;
//select the ith interval
int nonOverlap = below_lower_bound(intervals,
intervals.get(i).getBeginMinuteUnit());
if (nonOverlap >= 0)
max = dp[nonOverlap] + intervals.get(i).getIntervalMinute();
else
max = intervals.get(i).getIntervalMinute();
//do not select the ith interval
dp[i] = Math.max(max, dp[i-1]);
}
return dp[intervals.size() - 1];
}
public int below_lower_bound(List intervals, int startTime) {
int lb = -1, ub = intervals.size();
while (ub - lb > 1) {
int mid = (ub + lb) >> 1;
if (intervals.get(mid).getEndMinuteUnit() >= startTime)
ub = mid;
else
lb = mid;
}
return lb;
}
代码和最多区间调度最大的不同在选择第i个区间时。在这里用了一个二分查找来搜索不重叠的位置,然后判断该位置是否存在。如果不重叠位置存在,则算出当前的最大区间长度和;如果不存在,表明第i个区间和前面的所有区间均重叠,但由于我们还要选择第i个区间,所以暂时的最大区间和也即第i个区间自身的长度。在最多区间调度中,如果该位置不存在,我们直接将dp[i]赋值成dp[i-1],在这里我们却要将第i个区间本身的长度作为结果。从图五我们可以清楚地看到解释,在计算左下角的区间时,它和前面的两个区间都重合,但是它却包含在最优解中,因为它的长度比前面两个的和还要长。
这里求不重叠位置的时候,用了一个和c++中lower_bound函数类似的实现,和lower_bound的唯一差别在于返回的结果位置相差1。所以上述代码如果用C++来实现会更简单:
const int MAX_N=100000;
//输入
int N,S[MAX_N],T[MAX_N];
//用于对工作排序的pair数组
pair<int,int> itv[MAX_N];
void solve()
{
//对pair进行的是字典序比较,为了让结束时间早的工作排在前面,把T存入first,//把S存入second
for(int i=0;i<N;i++)
{
itv[i].first=T[i];
itv[i].second=S[i];
}
sort(itv,itv+N);
dp[0] = itv[0].first-itv[0].second;
for (int i = 1; i < N; i++)
{
int max;
//select the ith interval
int nonOverlap = lower_bound(itv, itv[i].second)-1;
if (nonOverlap >= 0)
max = dp[nonOverlap] + (itv[i].first-itv[i].second);
else
max = itv[i].first-itv[i].second;
//do not select the ith interval
dp[i] = max>dp[i-1]?max:dp[i-1];
}
printf(“%d\n”,dp[N-1]);
}
通过上面的分析,我们可以看出最大区间问题是一个应用范围更广的问题,最多区间调度问题是最大区间调度问题的一个特例。如果区间的长度都一样,则最大区间调度问题就退化为最多区间调度问题,进而可以利用更优的算法解决。一般的最大区间调度问题复杂度为: 排序$O(nlogn) $+扫描 $O(nlogn)=O(nlogn)$。
####3.3 带权的区间调度
该问题可以看作最大区间调度问题的一般化,也即我们不只是求区间长度和的最大值,而是再在每个区间上绑定一个权重,求加权之后的区间长度最大值。先看一个例子:某酒店采用竞标式入住,每一个竞标是一个三元组(开始,入住时间,每天费用)。现在有N个竞标,选择使酒店效益最大的竞标。(美团2013年)
该问题的目标变成了求收益的最大值,区间不重叠只是伴随必须满足的一个条件。但这不影响算法的适用性,最大区间调度问题的动态规划算法依旧适用于该问题,只不过是目标变了而已:**最大区间调度考虑的是区间长度和,而带权区间调度考虑的是区间的权重和,就是在区间的基础上乘以一个权重**,就这点差别。所以代码就很简单咯:
const int MAX_N=100000;
//输入
int N,S[MAX_N],T[MAX_N];
//用于对工作排序的pair数组
pair<int,int> itv[MAX_N];
void solve()
{
//对pair进行的是字典序比较,为了让结束时间早的工作排在前面,把T存入first,//把S存入second
for(int i=0;i<N;i++)
{
itv[i].first=T[i];
itv[i].second=S[i];
}
sort(itv,itv+N);
dp[0] = (itv[0].first-itv[0].second)*V[0];
for (int i = 1; i < N; i++)
{
int max;
//select the ith interval
int nonOverlap = lower_bound(itv, itv[i].second)-1;
if (nonOverlap >= 0)
max = dp[nonOverlap] + (itv[i].first-itv[i].second)*V[i];
else
max = (itv[i].first-itv[i].second)*V[i];
//do not select the ith interval
dp[i] = max>dp[i-1]?max:dp[i-1];
}
printf(“%d\n”,dp[N-1]);
}
博客介绍到这里,我们已经比较清楚上述三个问题的关系,带权区间调度应用最广,最大区间调度其次,最多区间调度应用范围最小。算法从通用的DP到特殊的DP再到贪心算法,难度逐渐降低。图六展示了三个问题的关系。

<div align = center>图6 三种调度问题的关系</div>
####3.4 最小区间覆盖
问题定义如下:有n 个区间,选择尽量少的区间,使得这些区间完全覆盖某给定范围[s,t]。
初次遇到该问题,大家可能会把该问题想得很复杂,是不是需要用最长的区间去覆盖给定的范围,然后将给定范围分割成两个更小的子问题,用递归去解决。这时我们就需要获得在给定范围内的最长区间,但是如何判断最长区间却有太多的麻烦,而且即使选择了在给定范围内的最长区间,也不见得能获得最优值。其实该问题根本就没有想象中麻烦,可能很容易地解决。
解决问题的关键在于,我们不要一开始就考虑整个范围,而是从给定范围的左端点入手。我们选择一个可以覆盖左端点的区间之后,就可以将左端点往右移动得到一个新的左端点。只要我们不停地选择可以覆盖左端点的区间就一定可以到达右端点,除非问题无解。关键是我们应该选择什么样的区间来覆盖左端点。由于我们要用选择区间的右端点和给定范围的左端点比较,所以第一想法会是先对所有的区间按照结束时间排序,然后按照结束时间从小到大和左端点比较。啥时候停止比较然后修改左端点呢?肯定是到了某个区间的开始时间大于给定范围的左端点的时候。这是因为如果我们继续遍历,可能就会不能完全覆盖给定范围。但是这样也可能会得不到最优解,如图七所示。
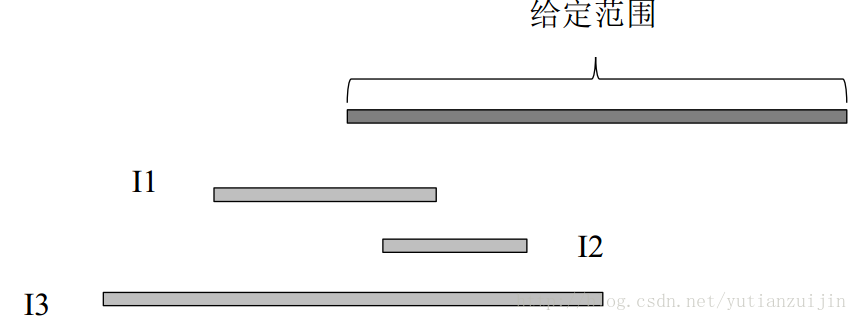
<div align = center>图7 按照结束时间排序的最小区间覆盖错误示意图</div>
在上图中,三个区间按照结束时间排序,第一个区间和给定范围的左端点相交,接着遍历第二个区间。这时发现第二个区间的左端点大于给定范围的左端点,这时我们就需要停止继续比较,修改给定范围新的左端点为end1。接着遍历第三个区间,按照上述规则我们就会将第三个区间也保留下来,但其实只需要第三个区间就满足要求了,第一个区间没有保留的意义,也即我们获得不了最优解。
既然按照结束时间获得不了最优解,我们再尝试按照开始时间排序看看。区间按照开始时间排序之后,我们从最小开始时间的区间开始遍历,**每次选择覆盖左端点的区间中右端点坐标最大的一个,并将左端点更新为该区间的右端点坐标,直到选择的区间已包含右端点。**按照这种方法我们就可以获得最优解,但是为什么呢?算法其实根据区间开始时间的值将区间进行了分组:在给定范围左端点左侧的和在左端点右侧的。由于我们按照开始时间排序,所以这两组区间的分界线很明确。而为了覆盖给定的范围,我们必须要从分界线左侧的区间中选一个(否则就不能覆盖整个范围)。上述算法选择了能覆盖给定范围左端点中右端点最大的区间,这是一个最优的选择。对剩余的区间都执行这样的选择显然可以获得最优解。
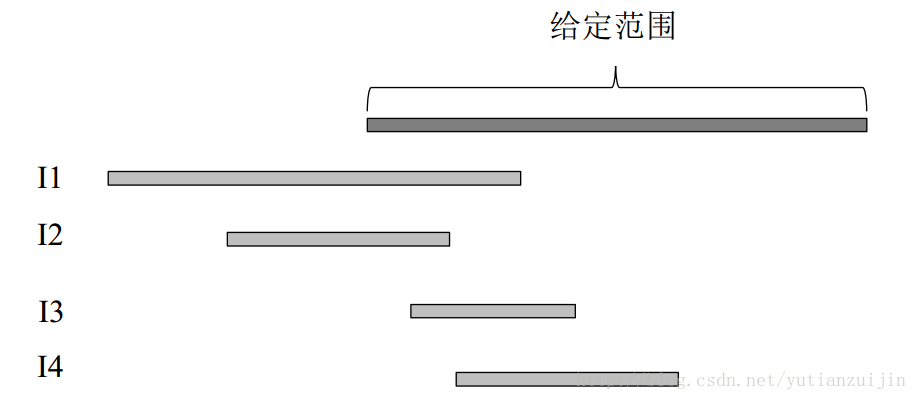
<div align = center>图8 按照开始时间排序的最小区间覆盖示意图</div>
图八给出一个示例。四个区间已经按照开始时间排序,我们从I1开始遍历。I1和I2都覆盖左端点,I3不覆盖,选择右端点最大的一个end1作为新的左端点,并且将I1添加到最小覆盖区间中。然后重复上述步骤,将剩余的区间和新的左端点比较并选择右端点最大的区间,修改左端点,这时左端点就会变为end4,I4添加到最小覆盖区间中。依次处理剩余的区间,我们就获得了最优解。代码实现如下:
const int MAX_N=100000;
//输入
int N,S[MAX_N],T[MAX_N];
//用于对工作排序的pair数组
pair<int,int> itv[MAX_N];
int solve(int s,int t)
{
for(int i=0;i<N;i++)
{
itv[i].first=S[i];
itv[i].second=T[i];
}
//按照开始时间排序
sort(itv,itv+N);
int ans=0,max_right=0;
for (int i = 0; i < N; )
{
//从开始时间在s左侧的区间中挑出最大的结束时间
while(itv[i].first<=s)
{
if(max_right<itv[i].end) max_right=itv[i].end;
i++;
}
if(max_right>s)
{
s=max_right;
ans++;
if(s>=t) return ans;
}
else //如果分界线左侧的区间不能覆盖s,则不可能有区间组合覆盖给定范围
{
return -1;
}
}
}
时间复杂度:排序$O(nlogn)$ +扫描$O(n) =O(nlogn)$ 。
###4. y轴上的区间调度
x轴上的区间调度关注的是区间在一维空间上的摆放(重叠或者不重叠),而y轴上的区间调度则将问题扩展到二维。虽然维度增加了,但是解决问题的难度没有增大多少。
####4.1 最大区间重叠(最少工人调度)
该问题似乎有两个矛盾的描述,既是最大又是最少,但其实是从不同的方面描述同一个问题。先看最大的一方面,问题可以这样描述:给定的n个区间,在任意时刻最多有几个重叠的区间,如图九所示,在12:00到12:30的范围内,最多有三个区间重叠,没有其他时刻超过三个区间重叠。WAP2013年的笔试题是从该角度考察该问题的([下载](http://download.csdn.net/download/yutianzuijin/8607053))。再看最少的一方面,假设我们将这些区间认为是一些工作,然后将这些工作分配给一些工人,每个工人不能同时干两件工作,最少需要几名工人。也即将所有的区间不重叠地摆在二维平面上,最少能够占据几行(很显然,可以一个工人干一件工作,这时n个工作就需要n个工人,也即在二维平面上一个工作占据一行,但显然不是最优的)。虽然该问题有两种理解方式,但是它们要解决的是同一个问题,所以解决方法相同。我们从最少工人调度角度看看如何解决该问题。
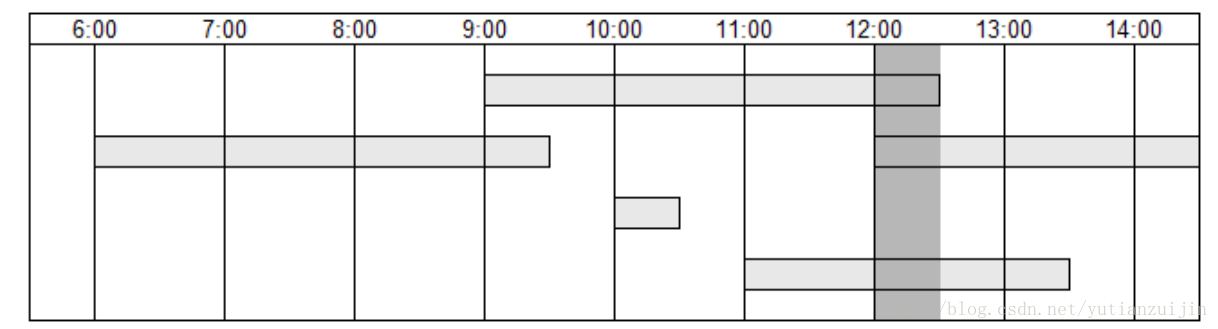
<div align = center>图9 最大区间重叠</div>
#####4.1.1 解法一
在最多区间调度中,我们分配尽可能多的不重叠工作给工人,这启发我们是否可以沿着这个思路去解决问题。按照最多区间调度分配不重叠工作给第一个工人,如果还有剩余工作,肯定需要别的工人来完成,我们继续按照最多区间调度问题来解,并分配一个新的工人,…,直到没有工作为止。很可惜,上面的策略不可行,请看图十。如果按照最多区间调度的策略分配工作,下面四个工作需要分配三个工人,但实际最少只需要两个工人即可。问题出在最多区间调度采用的是贪心算法,只要是下一个工作和目前的最大结束时间不重叠就选择该工作,这就导致在判断I3时将该工作分配给了第一个工人。

<div align = center>图10 按照最多区间调度的策略实现最少工人调度</div>
这是否意味着上述策略就彻底不行呢?只要稍微改改选择工人的策略还是可以的。当我们在判断一个工作该分配给哪个工人时,我们需要选择可以接受该工作同时完成之前的工作最晚的工人。例如,图十中判断I3该分配哪个工人。这时前两个工人都可以选择该工作,但是第二个工人完成之前的工作更晚,所以需要将I3分配给第二个工人,而不是第一个工人。这样分配工作的目的是让结束时间早的工人能处理后面未知的工作,而不是浪费在一个已知工作上。上述思路需要我们保存每个工人的上一个工作结束时间,也即下一个工作可以开始的时间。由于工作都按照结束时间排序,所以在添加新的工人时,我们会产生一个非递减的序列。但是当可以将新的工作分配给现有工人时,我们需要在有序序列中找到合适的位置,并修改该工人的可工作时间。为了维持序列的单调性,我们需要移动不少元素。按这种策略实现的java代码如下:
public int getMaxIntervalOverlapCount(List intervals) {
int maxWorkers = 0;
Collections.sort(intervals, new EndTimeComparator());
int[] endTime=new int[intervals.size()];
for(int i=0;i<intervals.size();i++)
{
int startTime=intervals.get(i).getBeginMinuteUnit();
int pos=below_lower_bound(endTime, maxWorkers, startTime);
if(pos==-1)
{
endTime[maxWorkers++]=intervals.get(i).getEndMinuteUnit();
}
else
{
for(int j=pos;j<maxWorkers-1;j++)
{
endTime[j]=endTime[j+1];
}
endTime[maxWorkers-1]=intervals.get(i).getEndMinuteUnit();
}
}
return maxWorkers;
}
public int below_lower_bound(int[] a,int n,int k) {
int lb = -1, ub = n;
while (ub - lb > 1) {
int mid = (ub + lb) >> 1;
if (a[mid] >= k)
ub = mid;
else
lb = mid;
}
return lb;
}
class EndTimeComparator implements Comparator<Object> {
public int compare(Object arg0, Object arg1) {
Interval i1 = (Interval) arg0;
Interval i2 = (Interval) arg1;
return i1.getEndHour() != i2.getEndHour() ? i1.getEndHour()
- i2.getEndHour() : i1.getEndMinute() - i2.getEndMinute();
}
}
上述算法可以获得最优解,复杂度为:排序$O(nlogn) $ +查找$O(nlogn) $ +扫描$O(n^2)= O(n^2)$。上述算法虽然可以获得最优解,但是复杂度和其他问题相比显然上升了一个量级,导致复杂度为$O(n^2)$的关键在于采用数组这种数据结构,找到合适的位置之后进行插入操作需要移动元素。如果采用平衡二叉树则会进一步降低复杂度到$O(nlogn)$ ,具体的实现大家可以自己尝试。
#####4.1.2 解法二
前面的解法按照结束时间排序,我们再看看按照开始时间排序是否可行。如图十一,四个工作已按照开始时间排序,我们看看如何将其分配给工人。既然按照开始时间排序,我们就从开始时间最小的工作开始分配。前三个工作肯定需要三个工人,关键是第四个工作该分配给谁。按照之前的策略,我们最好将I4和I2分配给同一个工人,这样分配I1工作的工人就可以分配其他未知的工作。如果采用这种策略,我们还是需要选择可以接受该工作同时完成之前的工作最晚的工人,这就意味着我们还是需要$O(n2)$的复杂度来解决问题。事实上,由于我们按照开始时间排序,所以后面未知工作的开始时间肯定会越来越晚,所以我们就不用担心该选择哪个工人的问题了,直接选择完成之前的工作结束时间最早的工人即可,也即将I1和I4分配给同一个工人。这样有什么好处呢?由于每次都是选择结束时间最早的工人,所以我们就可以选择一个最小堆来加速工人的寻找,从而降低整个算法的复杂度。
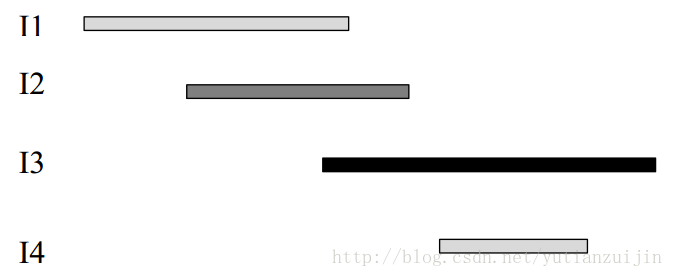
<div align = center>图11 按照开始时间排序实现最少工人调度</div>
具体的流程如下。我们用最小堆来维护一个工人完成之前工作的时间。当给新工作分配工人时,我们只需要将该工作的开始时间和堆顶的元素进行比较:如果堆顶的元素小于给定工作的开始时间,则可以将该工作分配给之前已经分配工作的工人,同时将堆顶元素修改成新工作的结束时间并重新调整堆;如果堆顶元素大于给定工作的开始时间,则表明目前分配工作的工人没有一个可以接受这个新工作,我们需要增加一个新的工人才行,同时往堆中增加该新工作的结束时间。按照这个思路实现的代码如下:
public int getMaxIntervalOverlapCount(List intervals) {
int maxWorkers = 0;
/*
* 1 check the parameter validity
*/
/*
* 2 sort the jobs(intervals) based on the start time
*/
Collections.sort(intervals, new StartTimeComparator());
/*
* 3 check the least number of needed workers
*/
PriorityQueue<Integer> pq = new PriorityQueue<Integer>(intervals.size());
// add the first job to the heap
pq.add(intervals.get(0).getEndMinuteUnit());
maxWorkers++;
for (int i = 1; i < intervals.size(); i++) {
// no allocated workers can do the next job
if (pq.peek() >= intervals.get(i).getBeginMinuteUnit()) {
maxWorkers++;
} else {
pq.poll();
}
pq.add(intervals.get(i).getEndMinuteUnit());
}
return maxWorkers;
}
class StartTimeComparator implements Comparator {
public int compare(Object arg0, Object arg1) {
Interval i1 = (Interval) arg0;
Interval i2 = (Interval) arg1;
return i1.getBeginHour() != i2.getBeginHour() ? i1.getBeginHour()
- i2.getBeginHour() : i1.getBeginMinute()
- i2.getBeginMinute();
}
}
上述算法可以获得最优解,复杂度为:排序$O(nlogn)$ +扫描$O(nlogn)=O(nlogn)$。和按照结束时间排序相比,复杂度并没有变化,但是理解上更容易了,所以往后遇到该问题如果对复杂度没有进一步的要求,解决方案就是:开始时间排序+最小堆。
#####4.1.3 解法三
算法的优化是永无止境的,该问题还有一个复杂度更低的解法,可以在排序之后将扫描的复杂度降到$O(n)$。核心的思想是将区间的开始和结束时间分开考虑,然后采用顺序扫描的方法即可获得最优解。具体的步骤为:将每个区间拆成两个事件点,按坐标从小到大排序,顺序处理每个区间。记录一个值 ,表示当前点被包含次数。每次遇到区间的左端点就+1,遇到右端点就-1。需要工人的数量就是在该过程中 的最大值。时间复杂度为排序$O(nlogn)$+扫描$O(n)=O(nlogn)$。这种解法的思路其实是从最大区间重叠的角度来考虑问题的,就介绍这么多,请自己实现代码。
**上面的三种解法都可以处理工人数没有限制的情况,但是如果限定工人的数目,然后看能选择多少区间(工作),则按照解法一会更方便。**因为当只有一个工人的时候,该问题等价于最多区间调度,所以按照最多区间调度的思路去解决该问题会更容易。
###5. 综合区间调度
在此我们简单介绍一下机器调度问题。机器调度问题和前面的区间调度问题很不一样。之前的调度问题中,给定的区间有一个固定的开始和结束时间,但是在机器调度中,每个区间或者叫任务都只包含一段执行时间,但是没有固定的开始时间。具体的问题描述如下:机器调度是指有m台机器需要处理n个作业,设作业i的处理时间为ti,则对n个作业进行机器分配,使得:
- 一台机器在同一时间内只能处理一个作业;
- 一个作业不能同时在两台机器上处理;
- 作业i一旦运行,则需要ti个连续时间单位。
设计算法进行合理调度,使得在m台机器上处理n个作业所需要的处理时间最短。如图十二,有三台机器,七个作业所需时间分别为(2,14,4,16,6,5,3),给出的调度最少需要17个单位时间。
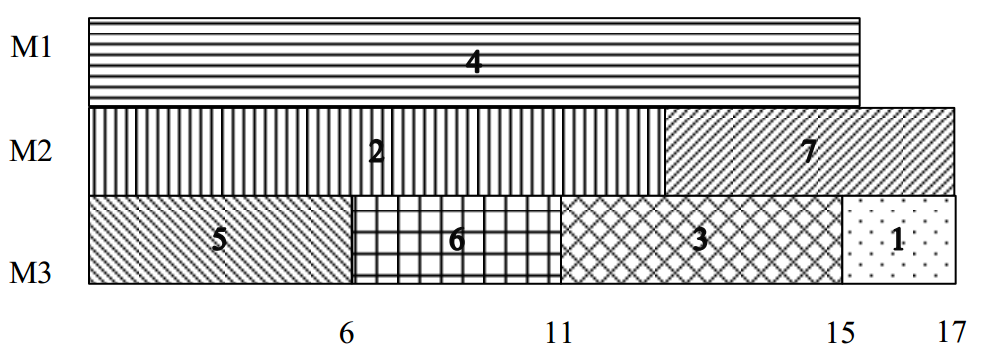
<div align = center>图12 三台机器的调度</div>
机器调度问题是一个NP-复杂问题,我们可以认为不存在多项式复杂度的解法获得最优解。如果非要获得最优解,我们必须要采用深搜策略遍历解空间,机器调度的解空间是一个k叉树,表示某个作业分配给哪一个机器;树共有n层,每一个叶节点表示一个可能的任务分配,最小的叶节点即是最优解,算法复杂度是$O(k^n)$。
针对NP复杂的问题,一般也不会让我们获得最优解,求个近似最优就好了。在机器调度中,采用一个称为最长处理时间优先(longest processing time first, LPT)的调度策略会获得较理想的调度方案。在LPT算法中,作业按照它们所需处理时间的递减顺序排序。在分配一个作业时,总是将其分配给最先变为空闲的机器。具体实现比较简单,就是先排序,然后采用最小堆维护一个最小开始时间即可,和最大区间重叠的方法二比较相似,具体不再赘述。
采用LPT策略有个定理:
令$\small F^{*}(I)$为在m台机器上执行作业集合I的最佳调度完成时间,F(I)为采用LPT调度策略所得到的调度完成时间,则
$$\small \frac{F(I)}{F^{*}(I)}\leqslant \frac{4}{3}-\frac{1}{3m}$$
可以看出,LPT策略和最优解很相近,是种比较好的近似策略。
###6. 总结
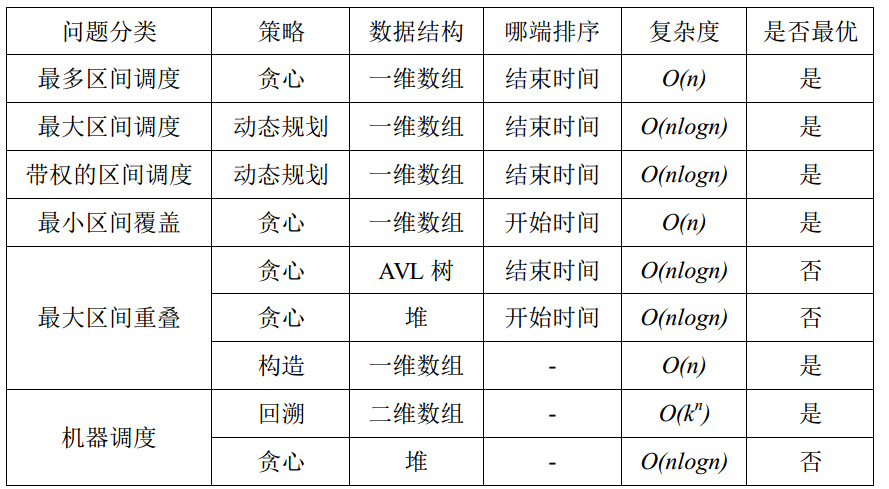
本博客详细介绍了几类区间调度问题,给出了最优解的思路和代码。虽然并没有完全覆盖区间调度问题,但是已足以让大家应对各种笔试面试。关于尚未触及的区间调度问题及相关例题,大家可进一步参考算法合集之《[浅谈信息学竞赛中的区间问题](https://wenku.baidu.com/view/7fcc174bc850ad02de80416b.html)》。下表给出了每个问题的最优解法以及复杂度(由于所有的问题都要先进行排序,所以我们只关注扫描的复杂度)。






















 1645
1645

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








