一、需求分析
1.题目要求
从命令行接受整数V和E,随机生成含有V个顶点和E条边的简单有向图,即不包含自环和平行边,存储结构无限定。对此有向图,运行实验求从一个随机选定的顶点可以到达的顶点数量的平均值。
2.输入输出
输入:顶点个数n、边个数e
输出:顶点出度平均值
二、概要设计
1.思路概述
本次实验中的图采用邻接矩阵存储,一方面操作简便,另一方面本章作业中存在传递闭包算法,在此可作为检验。
程序可分为两个部分:构建随机有向图、计算平均出度
构建随机有向图的思路:
-
根据输入顶点个数n,初始化邻接矩阵。
-
构建一个一维数组S作为辅助变量,大小size=n*(n-1)/2,即邻接矩阵中非对角线元素个数,用于存储随机数。
-
以时间为种子生成随机数(randomnum<=size)作为数组索引,若S[index]==0(处于初始状态),则S[index]=1。重复上述过程,共在数组内生成e个1,其余位不变(为0)。
-
将数组S中的数复制到邻接矩阵中,随机有向图构建完成。
计算平均出度的思路:
-
修改Floyd-Walshall算法,用于计算传递闭包。
-
在传递闭包中,若G[i][j]=1,则说明从i到j有一条路径。
-
统计传递闭包中所有为1的元素个数,除以顶点个数n,即为随机有向图的出度平均值
2.函数及调用
-
main():主函数,调用其他函数。
-
InitGraph(Mgraph* G, int n, int e):图的初始化函数
-
PrintGraph(Mgraph* G):打印图,方便调试与观察
-
RandomCreateGraph(Mgraph* G):构建随机图
-
Floyd_Warshall(Mgraph* G):利用Floyd-Warshall算法计算传递闭包
-
statistics(Mgraph* G):统计出度平均值
三、详细设计(伪代码)
1.main
int main()
{
Mgraph G;
InitGraph(&G,n,e);
RandomCreateGraph(&G);
Floyd_Warshall(&G);
statistics(&G);
return 0;
}2.RandomCreateGraph
void RandomCreateGraph(Mgraph* G)
{
int size=n*(n-1)
int S[size]
for (i = 0; i < size; i++)
S[i] = 0;
srand(time(NULL));
while (cnt <= G->e)
{
index = rand() % size;
if (S[index] == 0)
{
S[index] = 1;
cnt++;
}
}
for(int i=0;i<G->n;i++)
for (int j = 0; j < G->n; j++)
{
if (i != j)
{
G->edges[i][j] = S[cnt];
cnt++;
}
}
}3.Floyd_Warshall
void Floyd_Warshall(Mgraph* G)
{
for (int k = 0; k < G->n; k++)
for (int i = 0; i < G->n; i++)
for (int j = 0; j < G->n; j++)
{
if (i != k && j != k && i != j)
{
result = G->edges[k][j] * G->edges[i][k];
G->edges[i][j] = max(result,G->edges[i][j]);
}
}
}四、调试分析报告
1.时间复杂度:
-
PrintGraph:O(n^2)
-
InitGraph:O(n^2)
-
statistics:O(n^2)
-
RandomCreateGraph:O(n^2)
-
Floyd_Warshall:O(n^3)
-
综上:时间复杂度为O(n^3)
2.空间复杂度:
-
PrintGraph:O(1)
-
InitGraph:O(1)
-
statistics:O(1)
-
RandomCreateGraph:O(n*(n-1))
-
Floyd_Warshall:O(1)
-
综上:时间复杂度为O(n*(n-1))
五、用户使用说明
运行程序后,根据提示,依次输入顶点个数n和边个数e,以回车结束。随后程序将依次打印出随机创建的简单有向图和传递闭包以及平均出度。按任意键退出。
六、测试结果
1.n=3,e=6

2.n=5,e=7

3.n=10,e=13
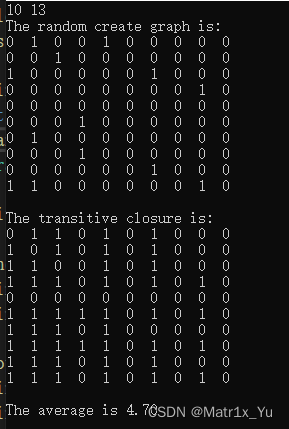
4.n=20,e=34

























 2758
2758

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










