在排序算法中快速排序的效率是非常高的,但是还有种排序算法的效率可以与之媲美,那就是归并排序;归并排序和快速排序有那么点异曲同工之妙,快速排序:是先把数组粗略的排序成两个子数组,然后递归再粗略分两个子数组,直到子数组里面只有一个元素,那么就自然排好序了,可以总结为先排序再递归;归并排序:先什么都不管,把数组分为两个子数组,一直递归把数组划分为两个子数组,直到数组里只有一个元素,这时候才开始排序,让两个数组间排好序,依次按照递归的返回来把两个数组进行排好序,到最后就可以把整个数组排好序;
算法分析
归并排序
是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
基本思路:
先递归的把数组划分为两个子数组,一直递归到数组中只有一个元素,然后再调用函数把两个子数组排好序,因为该函数在递归划分数组时会被压入栈,所以这个函数真正的作用是对两个有序的子数组进行排序;
基本步骤:
1、判断参数的有效性,也就是递归的出口;
2、首先什么都不管,直接把数组平分成两个子数组;
3、递归调用划分数组函数,最后划分到数组中只有一个元素,这也意味着数组是有序的了;
4、然后调用排序函数,把两个有序的数组合并成一个有序的数组;
5、排序函数的步骤,让两个数组的元素进行比较,把大的/小的元素存放到临时数组中,如果有一个数组的元素被取光了,那就直接把另一数组的元素放到临时数组中,然后把临时数组中的元素都复制到实际的数组中;
实现代码
#include<stdio.h>
#define LEN 12 // 宏定义数组的大小
static int tmp[LEN] = {0};// 设置临时数组
// 打印数组
void print_array(int *array)
{
int index = 0;
printf("\narray:\n");
for (; index < LEN; index++){
printf(" %d, ", *(array + index));
}
printf("\n");
}
// 把两个有序的数组排序成一个数组
void _mergeSort(int *array, int start, int middle, int end)
{
int first = start;
int second = middle + 1;
int index = start;
while ((first <= middle) && (second <= end)){
if (array[first] >= array[second])
tmp[index++] = array[second++];
else
tmp[index++] = array[first++];
}
while(first <= middle) tmp[index++] = array[first++];
while(second <= end) tmp[index++] = array[second++];
for (first = start; first <= end; first++)
array[first] = tmp[first];
}
// 递归划分数组
void mergeSort(int *array, int start, int end)
{
if (start >= end)
return;
int middle = ((end + start) >> 1);
mergeSort(array, start, middle);// 递归划分左边的数组
mergeSort(array, middle+1, end);// 递归划分右边的数组
_mergeSort(array, start, middle, end);// 对有序的两个数组进行合并成一个有序的数组
}
int main(void)
{
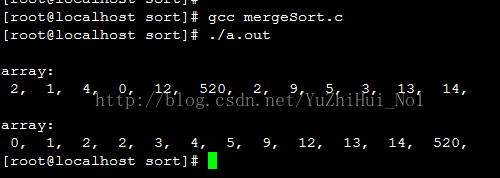
int array[LEN] = {2, 1, 4, 0, 12, 520, 2, 9, 5, 3, 13, 14};
print_array(array);
mergeSort(array, 0, LEN-1);
print_array(array);
return 0;
}
分析下上面代码:其实上面的代码主要的是两个函数,第一个是划分数组函数,第二个是对两个有序数组合并的归并函数;这里要借助一个临时数组,有的人在main函数中申请动态数组,然后让所有递归调用都使用该数组;也有的人在归并函数里申请个临时数组;而我的方法是定义一个全局的临时数组;其实我感觉这几个方法都是大同小异,因为不管是动态数组还是全局静态数组,在递归释放调用排序函数时,都会保存一份数据;如果是在排序函数中定义临时数组,那么应该和前面的方法一样的,因为是局部临时数组,存放在栈空间,当该函数调用完后,会马上释放。所以我个人感觉这三种方法都差不多(如果是在归并函数中定义的临时数组,则需要全部压栈;而其他的就只需要压入有用数据所占的空间就可以)
时间复杂度
归并的时间复杂度分析:主要是考虑两个函数的时间花销,一、数组划分函数
mergeSort();二、有序数组归并函数_
mergeSort();
_mergeSort()函数的时间复杂度为O(n),因为代码中有2个长度为n的循环(非嵌套),所以时间复杂度则为O(n);
简单的分析下元素长度为n的归并排序所消耗的时间 T[n]:调用mergeSort()函数划分两部分,那每一小部分排序好所花时间则为 T[n/2],而最后把这两部分有序的数组合并成一个有序的数组_mergeSort()函数所花的时间为 O(n);
公式:T[n] = 2T[n/2] + O(n);
公式就不仔细推导了,可以参考下: 排序算法之快速排序及其时间复杂度和空间复杂度里面时间复杂度的推导;
所以得出的结果为:T[n] = O( nlogn )
因为不管元素在什么情况下都要做这些步骤,所以花销的时间是不变的,所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为:O( nlogn );好像有人说最差的时间复杂度不是O(nlogn),我不知道怎么算出来的,知道的麻烦告知下,谢谢;
空间复杂度
归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间:n + logn;所以空间复杂度为: O(n)
以时间换空间
我看到网上很多blog分享空间复杂度只有O(1)的归并排序法;因为传统的归并排序所消耗的空间主要是在归并函数(把两个有序的函数合并成一个有序的函数),所以如果要让时间复杂度为 O(1) ,那么也只能在归并函数中做文章了。代码就不列出来了,其主要思想就是借助于快速排序(其实就是相当于归并函数被快速排序函数替换了);这样的方法虽然可以减少内存的消耗,但是却会在时间上带来损失,因为这样时间复杂度却变成了 O(n^2) 了;所以这种方法并不是一个两全其美的idea;
总结
归并排序虽然比较稳定,在时间上也是非常有效的(最差时间复杂度和最优时间复杂度都为 O(nlogn) ),但是这种算法很消耗空间,一般来说在内部排序不会用这种方法,而是用快速排序;外部排序才会考虑到使用这种方法;
转载请注明作者和原文出处,原文地址:http://blog.csdn.net/yuzhihui_no1/article/details/44223225
若有不正确之处,望大家指正,共同学习!谢谢!!!











 本文详细介绍了归并排序的原理和实现过程,包括基本思路、步骤、时间与空间复杂度分析等,并提供了完整的C语言实现代码。
本文详细介绍了归并排序的原理和实现过程,包括基本思路、步骤、时间与空间复杂度分析等,并提供了完整的C语言实现代码。
















 885
885

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








