数据结构-最小生成树-Prim算法

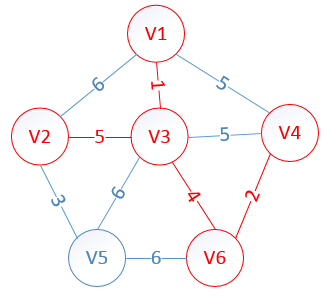
MST（Minimum Spanning Tree，最小生成树）问题有两种通用的解法，Prim算法就是其中之一，它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

初始状态：

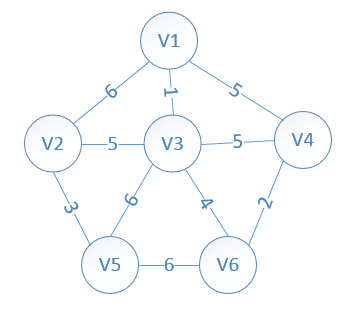
设置2个数据结构：

lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
mst[i]:表示对应lowcost[i]的起点，即说明边< mst[i],i>是MST的一条边，当mst[i]=0表示起点i加入MST

我们假设V1是起始点，进行初始化（*代表无限大，即无通路）：

lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=，lowcost[6]=

mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）

明显看出，以V3为终点的边的权值最小=1，所以边< mst[3],3>=1加入MST

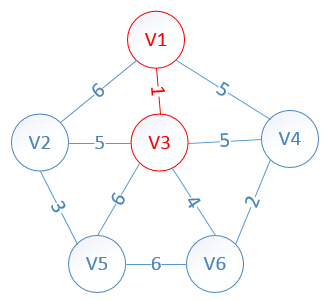
此时，因为点V3的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4

mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3

明显看出，以V6为终点的边的权值最小=4，所以边< mst[6],6>=4加入MST

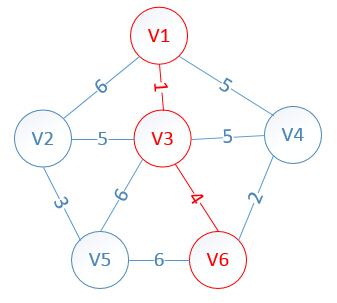
此时，因为点V6的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0

明显看出，以V4为终点的边的权值最小=2，所以边< mst[4],4>=4加入MST

此时，因为点V4的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=0，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=0，mst[5]=3，mst[6]=0

明显看出，以V2为终点的边的权值最小=5，所以边< mst[2],2>=5加入MST

此时，因为点V2的加入，需要更新lowcost数组和mst数组：

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=3，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=2，mst[6]=0

很明显，以V5为终点的边的权值最小=3，所以边< mst[5],5>=3加入MST

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=0，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=0，mst[6]=0

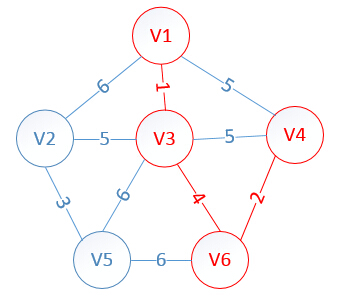
至此，MST构建成功，如图所示：

根据上面的过程，可以容易的写出具体实现代码如下（cpp）：

#include<iostream>
#include<fstream>
using  namespace std;

#define MAX 100
#define MAXCOST 0x7fffffff

int graph[MAX][MAX];

int prim(int graph[][MAX], int n)
{
    int lowcost[MAX];
    int mst[MAX];
    int i, j, min, minid, sum = 0;
    for (i = 2; i <= n; i++)
    {
        lowcost[i] = graph[1][i];
        mst[i] = 1;
    }
    mst[1] = 0;
    for (i = 2; i <= n; i++)
    {
        min = MAXCOST;
        minid = 0;
        for (j = 2; j <= n; j++)
        {
            if (lowcost[j] < min && lowcost[j] != 0)
            {
                min = lowcost[j];
                minid = j;
            }
        }
        cout << "V" << mst[minid] << "-V" << minid << "=" << min << endl;
        sum += min;
        lowcost[minid] = 0;
        for (j = 2; j <= n; j++)
        {
            if (graph[minid][j] < lowcost[j])
            {
                lowcost[j] = graph[minid][j];
                mst[j] = minid;
            }
        }
    }
    return sum;
}

int main()
{
    int i, j, k, m, n;
    int x, y, cost;
    ifstream in("input.txt");
    in >> m >> n;//m=顶点的个数，n=边的个数
    //初始化图G
    for (i = 1; i <= m; i++)
    {
        for (j = 1; j <= m; j++)
        {
            graph[i][j] = MAXCOST;
        }
    }
    //构建图G
    for (k = 1; k <= n; k++)
    {
        in >> i >> j >> cost;
        graph[i][j] = cost;
        graph[j][i] = cost;
    }
    //求解最小生成树
    cost = prim(graph, m);
    //输出最小权值和
    cout << "最小权值和=" << cost << endl;
    system("pause");
    return 0;
}

示例：灌溉问题

到了旱季农业生产的灌溉就成了一个大问题。为了保证灌溉的顺利，某县政府决定投资为各个村之间建立灌溉管道。

输入第1行包括一个整数N，表示某县的村庄的数量。（3≤N≤100），第2行-结尾为一个N×N的矩阵,表示每个村庄之间的距离。虽然在理论上，他们是N行，每行由N个用空格分隔的数组成，实际上，他们限制在80个字符，因此，某些行会紧接着另一些行。当然，对角线将会是0，因为不会有线路从第i个村到它本身（任何两个村之间的距离都不大于100000）。

输出只有一个，为修建灌溉管道将所有村庄相连在一个灌溉系统里所需的最小管道长度。

样例输入

4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0

样例输出

28

代码：

import java.util.Scanner;
public class Prim {
    static int n;
    static int [][]map;
    static int cost;
    static int MAXCOST=9999;
public static void main(String []args)
{
    Scanner scanner=new Scanner(System.in);
    n=scanner.nextInt();
    map=new int [n][n];
//  //初始化图G  
//    for (int i =0 ; i <n; i++)  
//    {  
//        for (int j =0 ; j <n; j++)  
//        {  
//            map[i][j] = MAXCOST;  
//        }  
//    }  
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            map[i][j]=scanner.nextInt();
        }
    }

    cost=prim(map);
    System.out.println(cost);

}
private static int prim(int[][] map2) {
 int lowcost[]=new int[n];//存储节点到MST的最短距离
 int mst[]=new int[n];//存储MST中到MST距离最近的点
 int i, j, min, minid, sum = 0; //sum为MST中距离的和
 //以节点0为初始结点
 for( i=1;i<n;i++)
 {
     lowcost[i]=map[0][i];
     mst[i]=0;//以节点0为初始结点
 }

 for(i=1;i<n;i++)//每次向MST中增加一个节点
 {
     min = Integer.MAX_VALUE;  
     minid = 0;  
     for(j=1;j<n;j++)//遍历n个节点,寻找一个距离MST最短的
     {
//       lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
         if(lowcost[j]<min&&lowcost[j]!=0)
         {
             minid = j; //找到一个距离MST距离最小的点j
             min = lowcost[j];  //点j距离MST的距离是min

         }
     }

 //  System.out.println("V"+mst[minid]+"-V"+minid+"="+min);
     sum += min;  
     lowcost[minid] = 0; //minid加入MST，更改lowcost[minid]为0

     //将找到的minid点加入MST后，更改其他节点的lowcost[i]

     for (j = 1; j < n; j++)  
     {  

         if (map[minid][j] < lowcost[j])  //若这个点到其他节点的距离小于其他节点到MST的距离
         {  
             lowcost[j] = map[minid][j];  
             mst[j] = minid;  
         }  
     }  

 }

    return sum;
}
}