机器学习-梯度下降

介绍

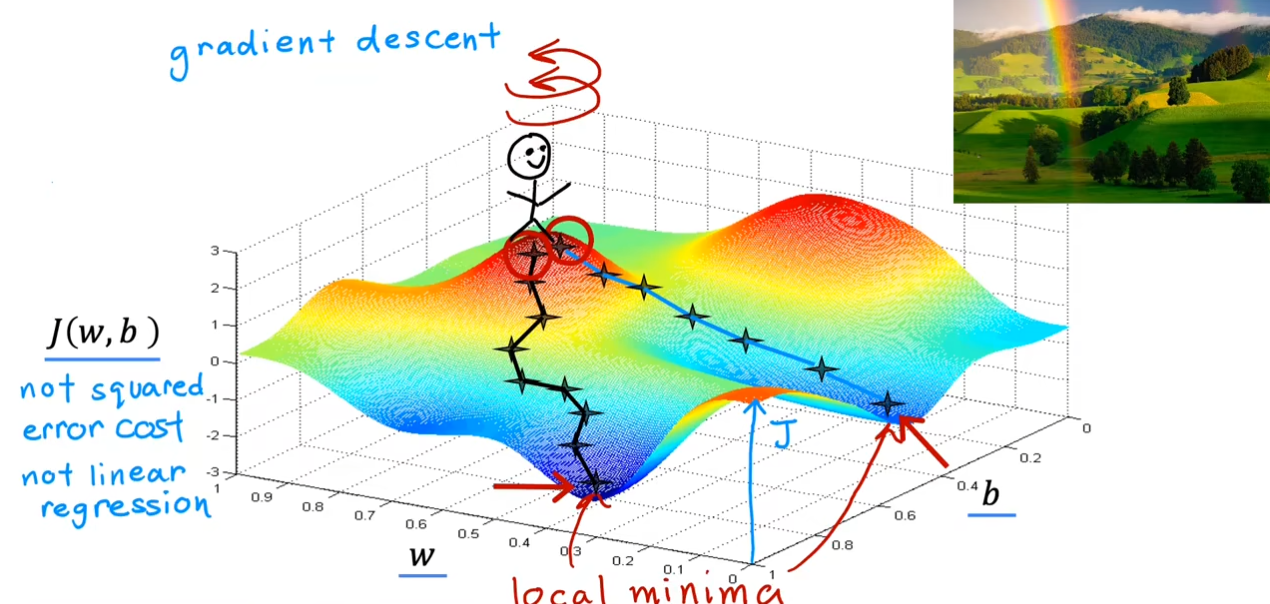
试想一下，你在一个山坡上寻找一个最快的下坡方法。首先$360$度旋转一周你会找到一个当前最陡峭的方向，沿着这个方向走一步。重复上面的操作，继续旋转$360$度，这个时候你会再次找到一个最陡峭的方向，重复该操作，直到你到达谷底。
同时，你可以选择$w,b$的值使得你的起始位置不同，从而可能到达不同的谷底，也就是局部最小值。

算法实现

通过公式$tm{p}_{-}w=w-\alpha \frac{\partial }{\partial w}J(w,b)$和$tm{p}_{-}b=b-\alpha \frac{\partial }{\partial b}J(w,b)$可以使得$w,b$的值不断更新，最终收敛于一个最小值$J(w,b)$。需要注意的是，$w,b$的值需要同时更新，注意这四行代码正确的执行顺序。

理解梯度下降

1. 从直观的$J(w)=wx$来理解，我们在此先忽略了$b$。

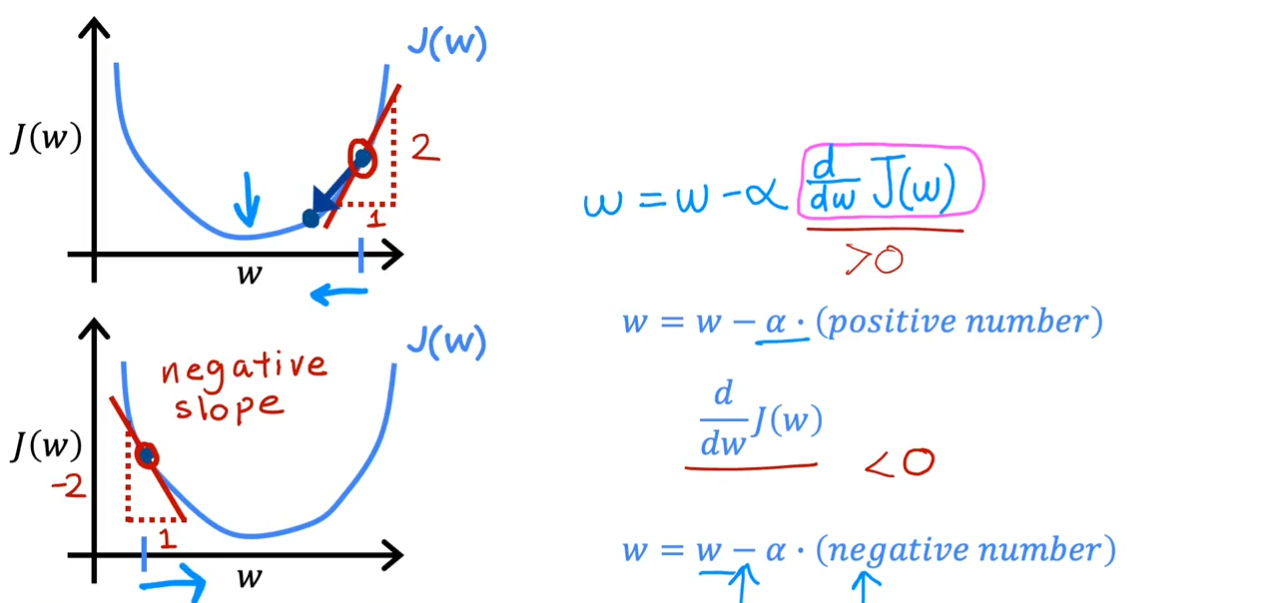
可以很清楚的看到，在第一幅图中，当我们关于$w$的偏微分为正数时，我们沿它的反方向也就是$x$轴的负方向，函数值会快速的下降。在第二幅图中，当我们沿$x$轴的正方向时，函数值也在快速下降，最终收敛于一个最小值。

2. 从多元函数微分的角度来理解

$J(w,b)=\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$
我们可以随意地给出一组$w,b$的取值，当然这样随意的值不会太理想，因此我们接下来要做的就是调整它们的值。我们可以求出损失函数$J(w,b)$对$w,b$的偏导数从而得到方向导数$\frac{\partial J}{\partial l}=\frac{\partial J}{\partial w}\cos \phi +\frac{\partial J}{\partial b}\sin \phi$，进而得到$J(w,b)$的梯度向量$(\frac{\partial J}{\partial w},\frac{\partial J}{\partial b})$。令向量$\vec{n}=(\frac{\partial J}{\partial W},\frac{\partial J}{\partial b})$，方向$l$的向量为$\vec{l}=(\cos \phi ,\sin \phi )$，因此$\frac{\partial \mathrm{J}}{\partial l}=\vec{n}\cdot \vec{l}=|n|\cdot |l|\cdot \cos \phi$。可以看到沿梯度方向时函数增长最陡峭的方向，$n$的模也就代表了它的陡峭程度，沿着这个向量的反方向去改变即可使$J(w,b)$下降的最快，直到最后几乎不再改变。

学习率

我们还有一个参数没有讨论，那就是$\alpha$，也被称为学习率，对于这个值，我们也应该选择一个合适的大小。

1. 过小

可以看到，当我们选择一个过小的$\alpha$时，我们的确也会到达收敛的最小值，但是需要花费的时间很长。

2. 过大

相比于过小，过大的情况可能会更加糟糕，如果我们第一次就越过了目标值，那么随着到达点的斜率越来越大，我们每次的距离可能就会越来越大，可能会出现像上面这种离我们需要的目标值越来越远的情况。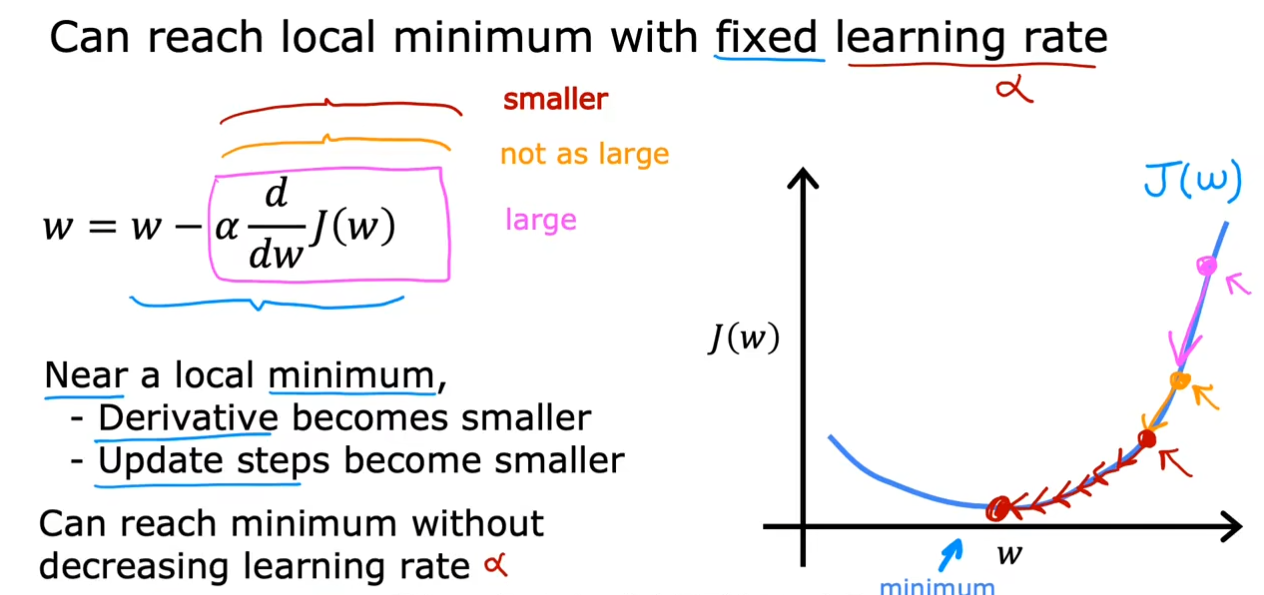

我们选择了一个固定大小的$\alpha$，即使我们不去调整它的值，随着我们逐渐下降，我们的倾斜程度也在逐渐减小，最终当变化速度为$0$时，我们就会固定在这个局部最小值。

用于线性回归的梯度下降

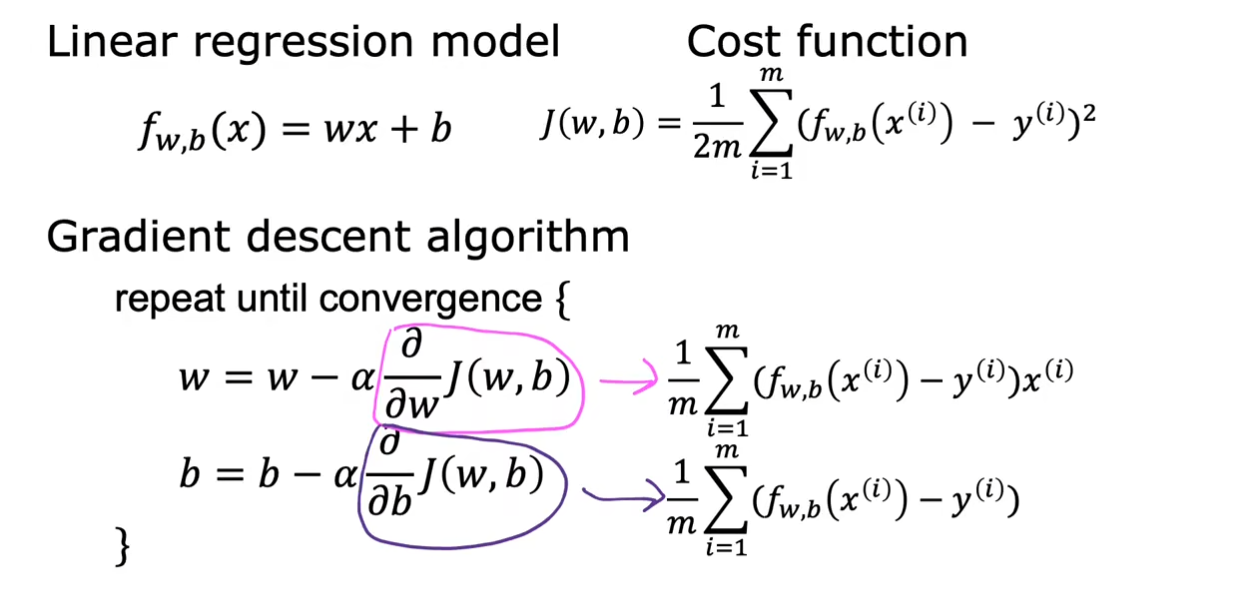
将前面的线性回归的代价函数$J(w,b)$带入这个梯度公式中，我们就得到了具体的值，这也解释了我们前面为什么对于代价函数除以$2$的疑问，这样使得计算更加美观。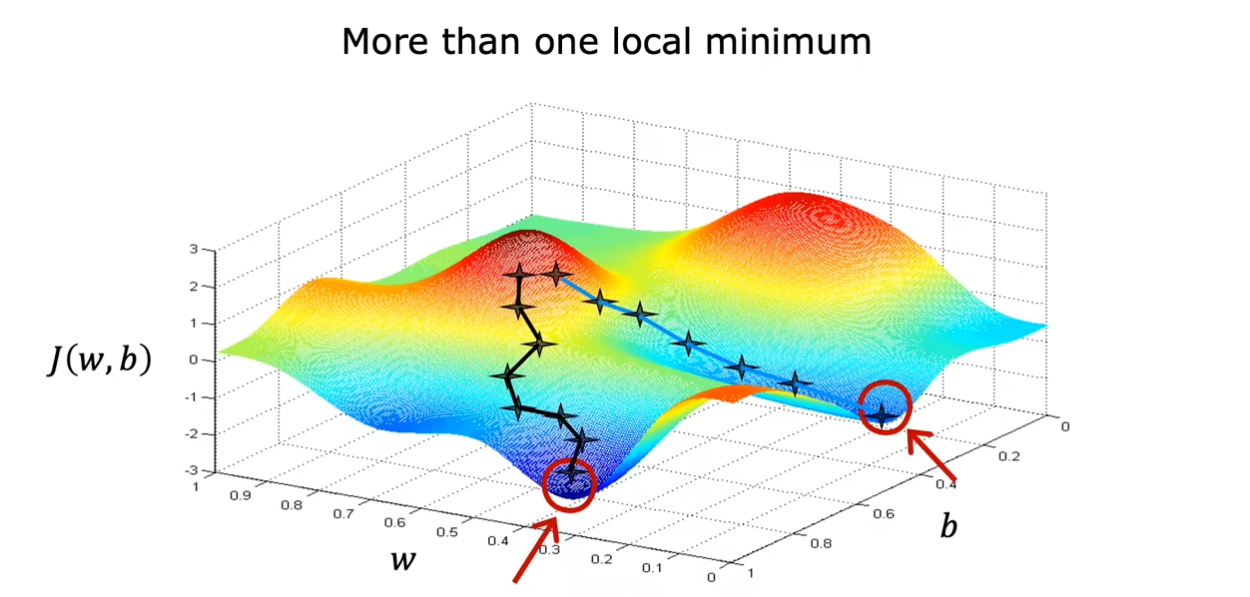

我们在前面提到过根据改变$w,b$的大小，我们可能会得到不同的局部最小值。不过幸运的是，在线性回归中，由于我们的图形是呈现一个碗状，因此我们不用担心这个问题，无论我们选择哪里都仅仅只有一个局部最小值。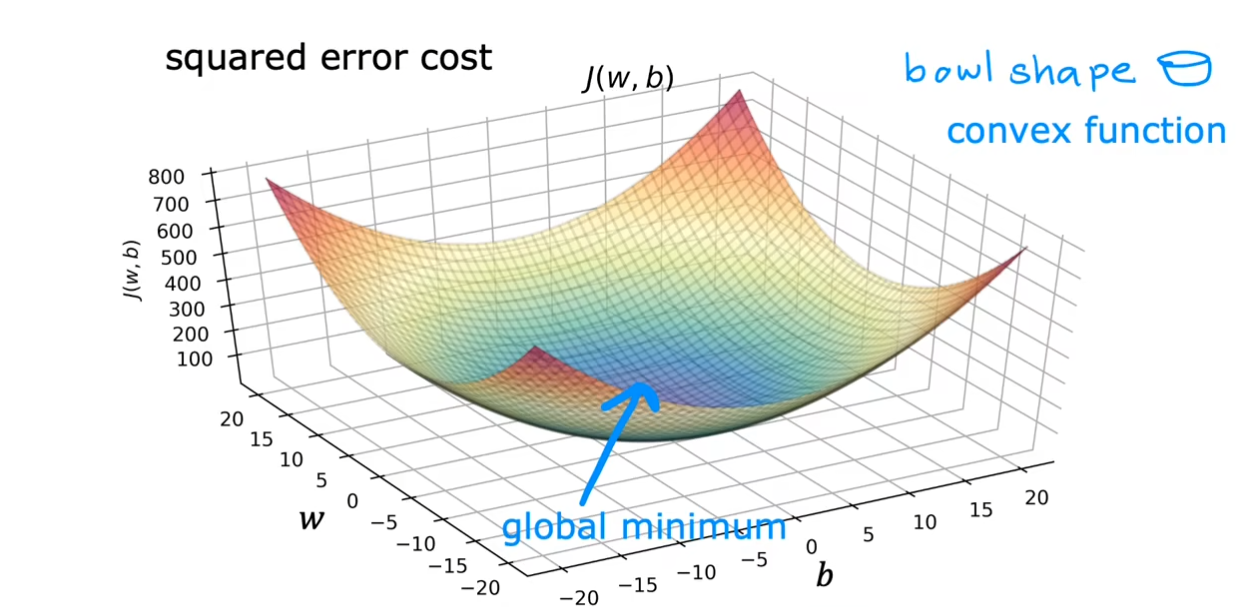

注意：这里没有打错，确实是凸函数，下面是维基百科的定义。

可以看到中国大陆对于凹函数和凸函数的定义与国外相反。

运行梯度下降

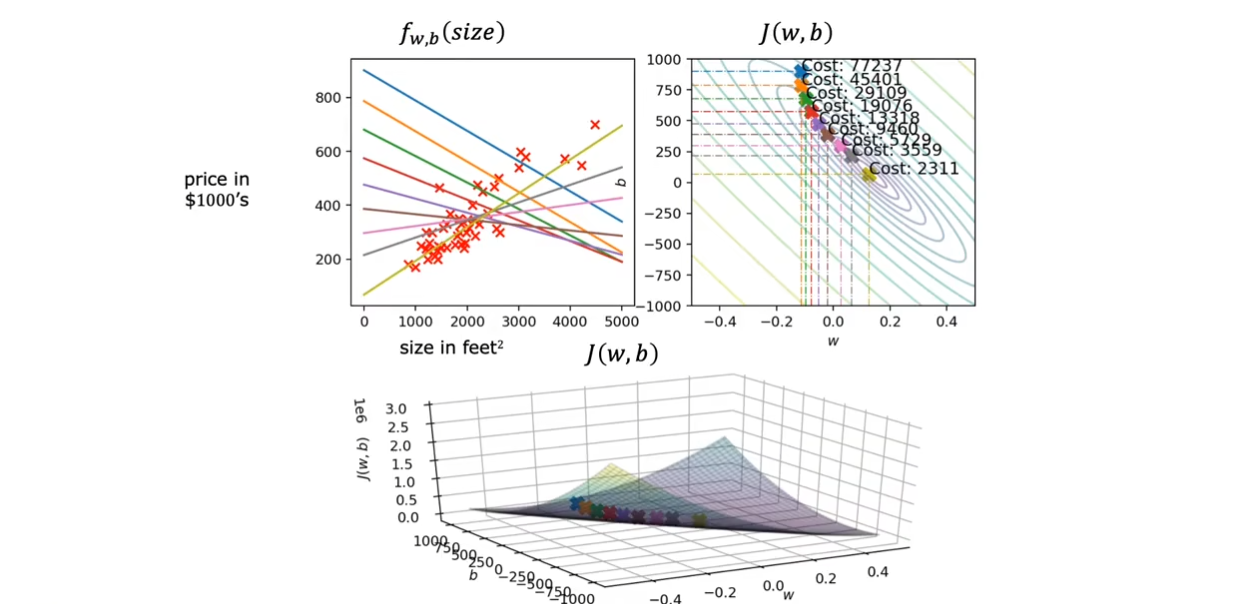
可以看到，通过对于$w,b$的调整，我们的函数越来越拟合数据，当我们到达全局最小值时，$f_{w,b}(size)$对于数据具有一个不错的拟合。

这种梯度下降方式也被称为批量梯度下降算法，在每次迭代过程中，使用整个整个数据集的梯度来更新模型参数，以最小化损失函数，进而得到模型的最优解。