从决策树到GBDT再到XGBoost

http://www.cnblogs.com/en-heng/p/5013995.html

决策树是一种通过对特征属性的分类对样本进行分类的树形结构，包括有向边与三类节点：

• 根节点（root node），表示第一个特征属性，只有出边没有入边；
• 内部节点（internal node），表示特征属性，有一条入边至少两条出边
• 叶子节点（leaf node），表示类别，只有一条入边没有出边。

上图就是二叉决策树的示例。最上面的是 Root node，中间的是 Internal node，最下面面和右边那些就是Leaf nodes.

决策树具有以下特点：

• 对于二叉决策树而言，可以看作是if-then规则集合，由决策树的根节点到叶子节点对应于一条分类规则;
• 分类规则是互斥并且完备的，所谓互斥即每一条样本记录不会同时匹配上两条分类规则，所谓完备即每条样本记录都在决策树中都能匹配上一条规则。
• 分类的本质是对特征空间的划分，如下图所示，

决策树学习的本质是从训练数据集中归纳出一组分类规则。

生成的决策树对训练数据会有很好的分类效果，却可能对未知数据的预测不准确，即决策树模型发生过拟合（overfitting）——训练误差（training error）很小、泛化误差（generalization error，亦可看作为test error）较大。下图给出训练误差、测试误差（test error）随决策树节点数的变化情况：

可以观察到，当节点数较小时，训练误差与测试误差均较大，即发生了欠拟合（underfitting）。当节点数较大时，训练误差较小，测试误差却很大，即发生了过拟合。只有当节点数适中是，训练误差居中，测试误差较小；对训练数据有较好的拟合，同时对未知数据有很好的分类准确率。

发生过拟合的根本原因是分类模型过于复杂，可能的原因如下：

• 训练数据集中有噪音样本点，对训练数据拟合的同时也对噪音进行拟合，从而影响了分类的效果；
• 决策树的叶子节点中缺乏有分类价值的样本记录，也就是说此叶子节点应被剪掉。

=======================================================================================================

http://www.cnblogs.com/en-heng/p/5035945.html

分类与回归树（Classification and Regression Trees, CART）是由四人帮Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出，既可用于分类也可用于回归。本文将主要介绍用于分类的CART。CART被称为数据挖掘领域内里程碑式的算法。

CART对特征属性进行二元分裂。特别地，当特征属性为标量或连续时，可选择如下方式分裂：

An instance goes left if CONDITION, and goes right otherwise

即样本记录满足CONDITION则分裂给左子树，否则则分裂给右子树。

标量属性

进行分裂的CONDITION可置为不等于属性的某值；比如，标量属性Car Type取值空间为{Sports, Family, Luxury}，二元分裂与多路分裂如下：

连续属性

CONDITION可置为不大于 ε ；比如，连续属性Annual Income，ε 取属性相邻值的平均值，其二元分裂结果如下：

===================================================================================================

http://www.jianshu.com/p/005a4e6ac775

 GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。
  GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。

Boosting Decision Tree：提升树算法

  提升树是迭代多棵回归树来共同决策。当采用平方误差损失函数时，每一棵回归树学习的是之前所有树的结论和残差，拟合得到一个当前的残差回归树，残差的意义如公式：残差 = 真实值 - 预测值 。提升树即是整个迭代过程生成的回归树的累加。

训练一个提升树模型来预测年龄：
  训练集是4个人，A，B，C，D年龄分别是14，16，24，26。样本中有购物金额、上网时长、经常到百度知道提问等特征。提升树的过程如下：

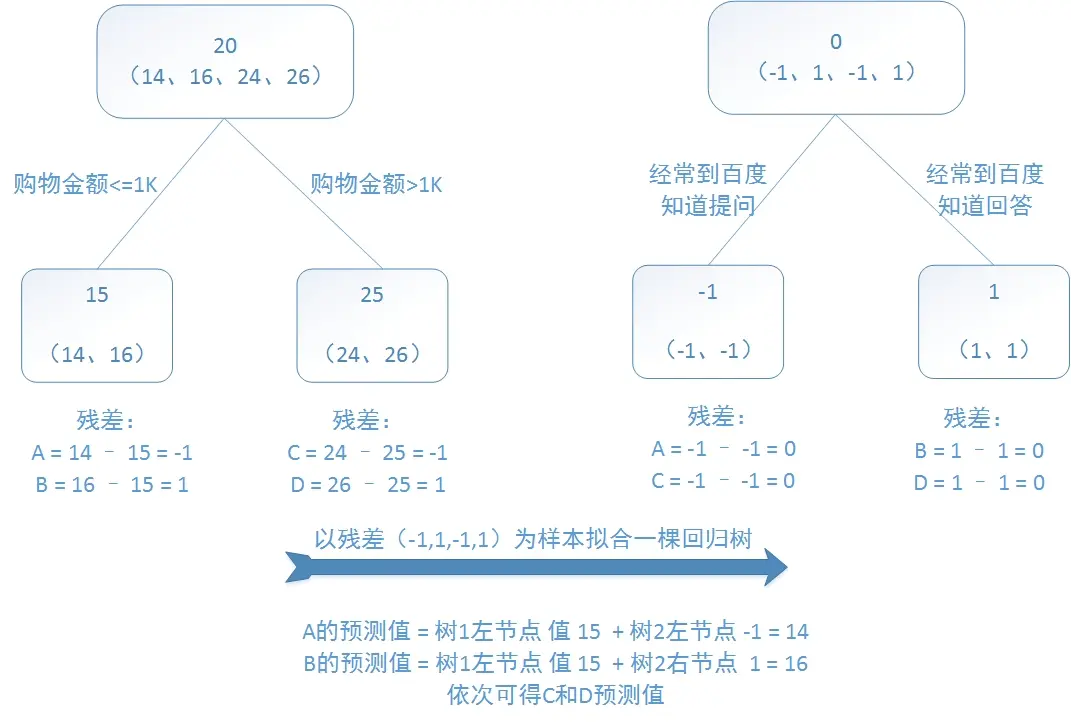
  该例子很直观的能看到，预测值等于所有树值得累加，如A的预测值 = 树1左节点 值 15 + 树2左节点 -1 = 14。
  因此，给定当前模型 fm-1(x)，只需要简单的拟合当前模型的残差。

Gradient Boosting Decision Tree：梯度提升决策树

  提升树利用加法模型和前向分步算法实现学习的优化过程。当损失函数是平方损失和指数损失函数时，每一步的优化很简单，如平方损失函数学习残差回归树。

 但对于一般的损失函数，往往每一步优化没那么容易，如上图中的绝对值损失函数和Huber损失函数。针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。

        随机森林(random forest)和GBDT都是属于集成学习（ensemble learning)的范畴。集成学习下有两个重要的策略Bagging和Boosting。
  Bagging算法是这样做的：每个分类器都随机从原样本中做有放回的采样，然后分别在这些采样后的样本上训练分类器，然后再把这些分类器组合起来。简单的多数投票一般就可以。其代表算法是随机森林。Boosting的意思是这样，他通过迭代地训练一系列的分类器，每个分类器采用的样本分布都和上一轮的学习结果有关。其代表算法是AdaBoost, GBDT。

  对于Bagging算法来说，由于我们会并行地训练很多不同的分类器的目的就是降低这个方差(variance) ,因为采用了相互独立的基分类器多了以后，h的值自然就会靠近.所以对于每个基分类器来说，目标就是如何降低这个偏差（bias),所以我们会采用深度很深甚至不剪枝的决策树。
  对于Boosting来说，每一步我们都会在上一轮的基础上更加拟合原数据，所以可以保证偏差（bias）,所以对于每个基分类器来说，问题就在于如何选择variance更小的分类器，即更简单的分类器，所以我们选择了深度很浅的决策树。

===================================================================================================================

xgboost是Gradient Boosting的一种高效系统实现，并不是一种单一算法。xgboost里面的基学习器除了用tree(gbtree)，也可用线性分类器(gblinear)。而GBDT则特指梯度提升决策树算法。
xgboost相对于普通gbm的实现，可能具有以下的一些优势：

1. 显式地将树模型的复杂度作为正则项加在优化目标
2. 公式推导里用到了二阶导数信息，而普通的GBDT只用到一阶
3. 允许使用column(feature) sampling来防止过拟合，借鉴了Random Forest的思想，sklearn里的gbm好像也有类似实现。

4.实现了一种分裂节点寻找的近似算法，用于加速和减小内存消耗。
5.节点分裂算法能自动利用特征的稀疏性。
6.data事先排好序并以block的形式存储，利于并行计算
7.cache-aware, out-of-core computation，这个我不太懂。。
8.支持分布式计算可以运行在MPI，YARN上，得益于底层支持容错的分布式通信框架rabit。

链接：https://www.zhihu.com/question/41354392/answer/91371364