命题逻辑-C语言-CSDN博客

本文链接：https://blog.csdn.net/z383101168/article/details/145320118

文章目录

一、练习题目-命题逻辑
二、程序设计与开发
三、源代码
三、总结反思

一、练习题目-命题逻辑

1.1 练习内容

（1）求任意一个命题公式的真值表。
（2）利用真值表求任意一个命题公式的主范式。
（3）判断两个命题公式是否等值。

1.2 练习目的

真值表是命题逻辑中的一个十分重要的概念，利用它几乎可以解决命题逻辑中的所有问题。例如，利用命题公式的真值表，可以判断命题公式的类型、求命题公式的主范式、判断两命题公式是否等价，还可以进行推理等。
本练习通过编写一个程序，让计算机给出命题公式的真值表，并在此基础上进行命题公式类型的判定、求命题公式的主范式等。目的是让学生更加深刻地理解真值表的概念，并掌握真值表的求解方法及其在解决命题逻辑中其他问题中的应用。

1.3 算法的主要思想

利用计算机求命题公式真值表的关键是：

① 给出命题变元的每一组赋值；
② 计算命题公式在每一组赋值下的真值。

真值表中命题变元的取值具有如下规律：

每列中0和1是交替出现的，且0和1连续出现的个数相同。n个命题变元的每组赋值的生成算法可基于这种思想。

含有n个命题变元的命题公式的真值的计算采用的方法为“算符优先法”。

为了程序实现的方便，约定命题变元只用一个字母表示，非、合取、析取、条件和双条件联结词分别用！、&、|、－、＋来表示。

算符之间的优先关系如表所示：

	+	-	\|	&	!	(	)	@
+	>	<	<	<	<	<	>	>
-	>	>	<	<	<	<	>	>
\|	>	>	>	<	<	<	>	>
&	>	>	>	>	<	<	>	>
!	>	>	>	>	>	<	>	>
(	<	<	<	>	<	<	=	E
)	>	>	>	>	>	E	>	>
@	<	<	<	<	<	<	E	=

为实现算符优先算法，我们采用两个工作栈：

一个称作OPTR，用以寄存运算符；
另一个称作OPND，用以寄存操作数或运算结果。

算法的基本思想是：
（1）首先设置操作数栈为空栈，符号“@”为运算符的栈底元素；
（2）调用函数Divi（exp，myopnd）得到命题公式包含的命题变元序列myopnd（按字典序排列，同一个命题变元只出现一次）；
（3）依次读入命题公式中的每个字符，若是命题变元则其对应的赋值进OPND栈，若是运算符，则和OPTR栈的栈顶运算符比较后作相应操作，直至整个命题公式求值完毕。

利用计算机求命题公式主析取范式和主合取范式的关键是：
命题公式在每一组赋值下的真值。如果全为假，那么该命题公式为矛盾式，它的主析取范式为0；如果全为真，那么该命题公式为重言式，它的主合取范式为1。否则遍历各种情况，主析取范式为m加命题公式在所有赋值情况下真值为1的该元素的数组下标的析取；主合取范式则是M加真值为0
的该元素的数组下标的合取。

利用计算机求两个命题公式是否等值的关键是：
判断其中一个命题双条件另一个命题，这个总的命题在每一组赋值下的真值是否全为真，如果是则等值，否则不等值。

二、程序设计与开发

2.1 系统总功能

（1）求任意一个命题公式的真值表。
（2）利用真值表求任意一个命题公式的主范式。
（3）判断两个命题公式是否等值。

2.2 程序流程图

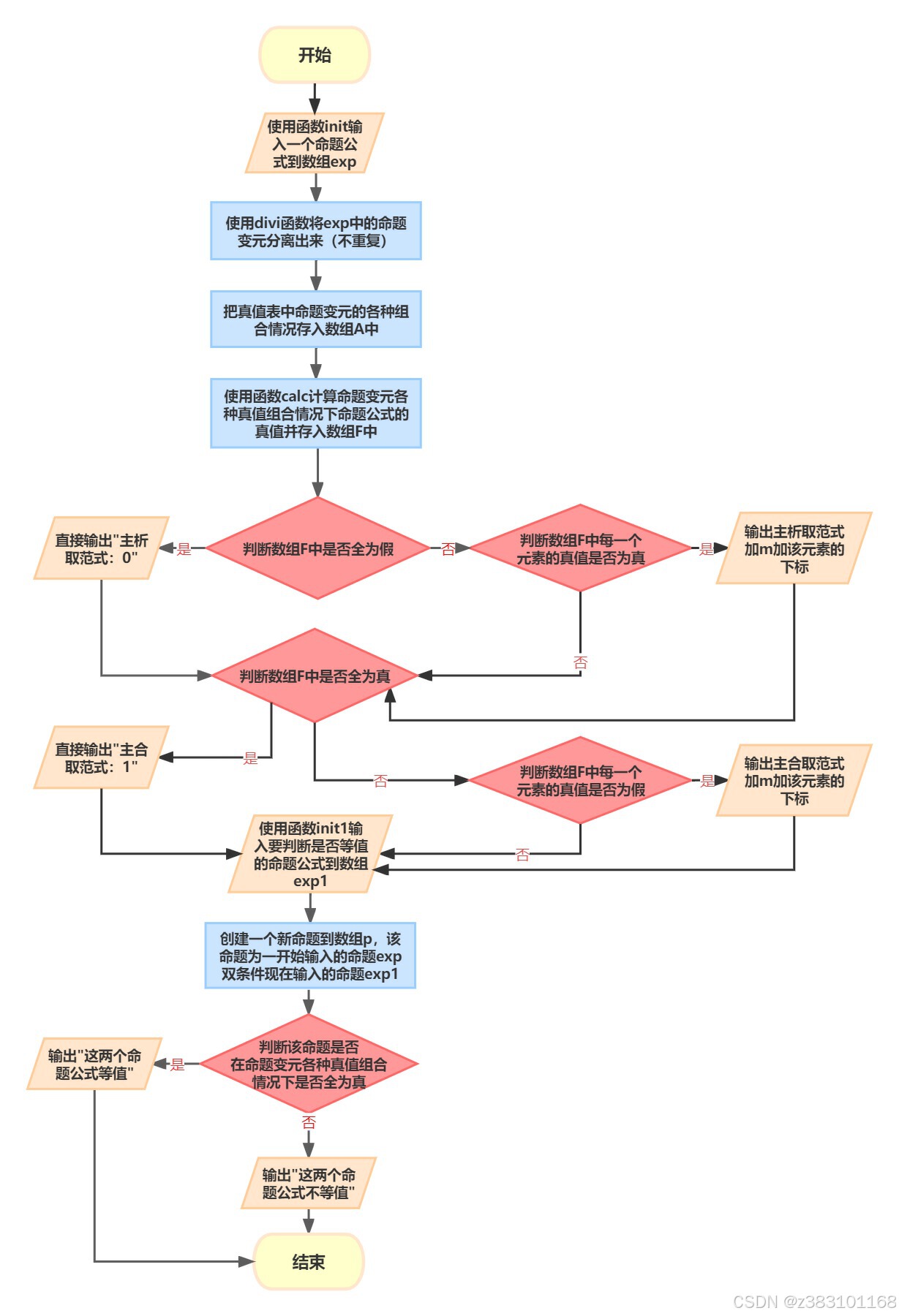
在这里插入图片描述

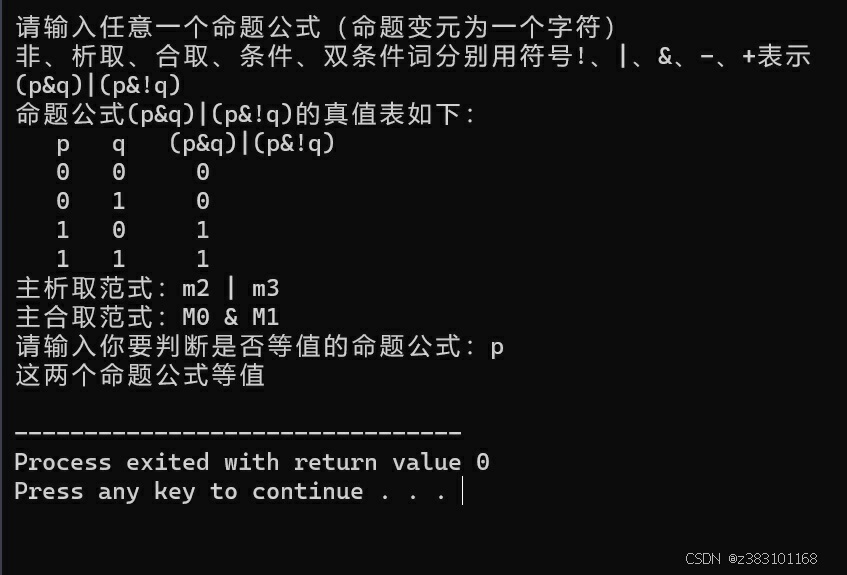
2.3 系统测试

对系统进行了简单的测试，演示截图包括：

请添加图片描述

在这里插入图片描述

三、源代码

#include "stdio.h"
#include <math.h>
#include <string.h>
typedef struct optrstack
{
	char oper[30];
	int loc;
} OPStack;
void initop(OPStack &op)
{
	int i;
	op.loc = 0;
	for (i = 0; i < 30; i++)
		op.oper[i] = '\0';
}
void push(OPStack &op, char c)
{
	op.oper[op.loc++] = c;
}
char pop(OPStack &op)
{
	return (op.oper[--op.loc]);
}
typedef struct opndstack
{
	int oper[60];
	int loc;
} OPndStack;
void initopnd(OPndStack &op)
{
	int i;
	op.loc = 0;
	for (i = 0; i < 30; i++)
		op.oper[i] = '\0';
}
void pushopnd(OPndStack &op, int c)
{
	op.oper[op.loc++] = c;
}
int popopnd(OPndStack &op)
{
	return (op.oper[--op.loc]);
}
void init(char s[])
{
	int t;
	printf("\n请输入任意一个命题公式（命题变元为一个字符）\n");
	printf("非、析取、合取、条件、双条件词分别用符号!、|、&、-、+表示\n");
	gets(s);
	t = strlen(s);
	s[t] = '@';
	s[t + 1] = '\0';
}
void init1(char s[])
{
	int t;
	gets(s);
	t = strlen(s);
	s[t] = '@';
	s[t + 1] = '\0';
}
int is_optr(char c)
{
	char optr_list[] = "+-|&!()@";
	for (int i = 0; i < (int)strlen(optr_list); i++)
		if (c == optr_list[i])
			return 1;
	return 0;
}
char first(char op1, char op2)
{
	char tab[8][9] = {
		"><<<<<>>",
		">><<<<>>",
		">>><<<>>",
		">>>><<>>",
		">>>>><>>",
		"<<<<<<=E",
		">>>>>E>>",
		"<<<<<<E=",
	};
	char optr_list[] = "+-|&!()@"; //双条件、条件、析取、合取、非
	int op1_loc, op2_loc;
	for (op1_loc = 0; op1_loc < (int)strlen(optr_list); op1_loc++)
		if (optr_list[op1_loc] == op1)
			break;
	for (op2_loc = 0; op2_loc < (int)strlen(optr_list); op2_loc++)
		if (optr_list[op2_loc] == op2)
			break;
	return tab[op1_loc][op2_loc];
}
int operate(int x, char op, int y)
{
	switch (op)
	{
	case '+':
		return (((!x) || y) && (x || (!y)));
		break;
	case '-':
		return ((!x) || y);
		break;
	case '|':
		return x || y;
		break;
	case '&':
		return x && y;
		break;
	}
	return -1;
}
void divi(char s[], char c[])
{
	int i, j = 0, t;
	for (i = 0; s[i] != '@'; i++)
		if (!is_optr(s[i]))
		{
			for (t = 0; t < j; t++)
				if (c[t] == s[i])
					break;
			if (t == j)
				c[j++] = s[i];
		}
	c[j] = '\0';
	char aa;
	for (i = 0; i < j - 1; i++) //按字典序排序
		for (t = i + 1; t < j; t++)
			if (c[i] > c[t])
			{
				aa = c[i];
				c[i] = c[t];
				c[t] = aa;
			}
}
int locate(char s[], char c)
{
	int i;
	for (i = 0; i < (int)strlen(s); i++)
		if (s[i] == c)
			break;
	return i;
}
int calc(char s[100], int *p)
{
	char myopnd[10], c;
	int sloc = 0;
	OPStack optr;
	initop(optr);
	push(optr, '@');
	OPndStack opnd;
	initopnd(opnd);
	divi(s, myopnd);
	c = s[sloc++];
	while (c != '@' || optr.oper[optr.loc - 1] != '@')
	{
		if (!is_optr(c))
		{
			int d1;
			d1 = p[locate(myopnd, c)];
			pushopnd(opnd, d1);
			c = s[sloc++];
		}
		else
		{
			switch (first(optr.oper[optr.loc - 1], c))
			{
			case '<':
				push(optr, c);
				c = s[sloc++];
				break;
			case '=':
				pop(optr);
				c = s[sloc++];
				break;
			case '>':
				char op;
				op = pop(optr);
				if (op == '!')
				{
					int a;
					a = !popopnd(opnd);
					pushopnd(opnd, a);
				}
				else
				{
					int a, b;
					a = popopnd(opnd);
					b = popopnd(opnd);
					int res;
					res = operate(b, op, a);
					pushopnd(opnd, res);
				}
				break;
			}
		}
	}
	return opnd.oper[opnd.loc - 1];
}
int main()
{
	char exp[100], myopnd[10];
	int i, j, n, m, A[1024][10], flag, k;
	int F[1024];
	init(exp);
	divi(exp, myopnd);
	n = (int)strlen(myopnd);
	m = (int)pow(2, n);
	for (j = 0; j < n; j++)
	{
		flag = 1;
		k = (int)pow(2, n - j - 1);
		for (i = 0; i < m; i++)
		{
			if (!(i % k))
				flag = !flag;
			if (flag)
				A[i][j] = 1;
			else
				A[i][j] = 0;
		}
	}
	char ss[100];
	int t;
	strcpy(ss, exp);
	t = (int)strlen(ss);
	ss[t - 1] = '\0';
	printf("命题公式%s的真值表如下：\n", ss);
	for (j = 0; j < n; j++)
		printf("%4c", myopnd[j]);
	printf("   %s\n", ss);
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < n; j++)
			printf("%4d", A[i][j]);
		F[i] = calc(exp, A[i]);
		printf("%6d", F[i]);
		printf("\n");
	}
	printf("主析取范式：");
	//矛盾式的主析取范式为0
	int flag1 = 0;
	for (i = 0; i < m; i++)
	{
		if (F[i])
		{
			flag1 = 1;
		}
	}
	if (!flag1)
	{
		printf("0");
	}
	else
	{
		for (i = 0; i < m; i++)
		{
			if (F[i])
			{
				printf("m%d", i);
				for (j = i + 1; j < m; j++)
				{
					if (F[j])
					{
						printf(" | ");
						break;
					}
				}
			}
		}
	}
	printf("\n");
	printf("主合取范式：");
	//重言式的主合取范式为1
	flag1 = 0;
	for (i = 0; i < m; i++)
	{
		if (!F[i])
		{
			flag1 = 1;
		}
	}
	if (!flag1)
	{
		printf("1");
	}
	else
	{
		for (i = 0; i < m; i++)
		{
			if (!F[i])
			{
				printf("M%d", i);
				for (j = i + 1; j < m; j++)
				{
					if (!F[j])
					{
						printf(" & ");
						break;
					}
				}
			}
		}
	}
	printf("\n");
	printf("请输入你要判断是否等值的命题公式：");
	char exp1[100];
	init1(exp1);
	int t1 = (int)strlen(exp1);
	char p[200];
	p[0] = '(';
	for (i = 1; i < t1 + t + 4; i++)
	{
		if (i < t)
		{
			p[i] = exp[i - 1];
		}
		else if (i == t)
		{
			p[i] = ')';
		}
		else if (i == t + 1)
		{
			p[i] = '+';
		}
		else if (i == t + 2)
		{
			p[i] = '(';
		}
		else if ((i < t1 + t + 2) && (i > t + 2))
		{
			p[i] = exp1[i - t - 3];
		}
		else if (i == t1 + t + 2)
		{
			p[i] = ')';
		}
		else if (i == t1 + t + 3)
		{
			p[i] = '@';
		}
	}
	divi(p, myopnd);
	n = (int)strlen(myopnd);
	m = (int)pow(2, n);
	for (j = 0; j < n; j++)
	{
		flag = 1;
		k = (int)pow(2, n - j - 1);
		for (i = 0; i < m; i++)
		{
			if (!(i % k))
			{
				flag = !flag;
			}
			if (flag)
			{
				A[i][j] = 1;
			}
			else
			{
				A[i][j] = 0;
			}
		}
	}
	flag = 1;
	for (i = 0; i < m; i++)
	{
		if (!calc(p, A[i]))
		{
			flag = 0;
			printf("这两个命题公式不等值\n");
			break;
		}
	}
	if (flag)
	{
		printf("这两个命题公式等值\n");
	}
	return 0;
}

三、总结反思

本程序实现了求任意一个命题公式的真值表、主析取范式和主合取范式，并判断两个命题公式是否等值。通过这次大作业，我学到了许多东西，这次大作业将离散数学的知识与编程相结合，使我对命题逻辑这方面的知识有了更加深刻的理解。
一开始在编写代码的过程中，虽然运行上没有什么报错，但是在测试时却发现了一些问题。比如一开始我没考虑到重言式和矛盾式的情况，因此直接运行时重言式的主合取范式和矛盾式的主析取范式的输出都是空的。在发现了这个问题后，我对程序加了一个判断，在输出主合取范式和主析取范式时分别判断命题公式是否为重言式和矛盾式，如果是则直接分别直接输出1和0就可以了。
其次这个程序可以判断一个只含有一个命题变元的命题公式和一个含有两个命题变元的命题公式是否等值，例如可以判断p与(p&q)|(p&!q)这两个命题公式是等值的。
但与此同时，这个程序也有不足之处，就是没有输出含有命题变元的主析取范式和主合取范式，只是输出用m或M加下标来表示，对此我的改进方法是通过m或M加下标这些已有的来分别输出它们对应的含有命题变元的极小项和极大项。
通过这次大作业的练习，我受益匪浅，感受到了真值表的用途之广泛，不仅对离散数学的知识理解更加深刻，对于编程方面也学到了许多新的知识，在一定程度上提高了逻辑思维能力，收益颇丰。