计算几何之向量叉积

1. 叉积定义

       p1 * p2 = det [p1 p2] = x1y2 - x2y1

            若对于原点(0, 0) 来说, 

            (1) 若 result > 0, 则 p1 位于 p2 的顺时针方向；

            (2) 若result < 0, 则 p1 位于 p2 的逆时针方向;  

            (3) 若 result = 0, 则 p1 与 p2 共线。（注意有可能同向或反向，若要判断方向，可用向量点积判断）

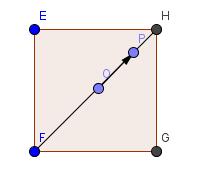
            下面图1，表示两个向量的位置关系，阴影部分的面积表示叉积的结果；图2，向量 OP 左上角表示OP 的逆时针方向, 右下角表示顺时针方向, 注意不包括共线部分。

2. 叉积意义

         （1）向量叉积的运算结果是平行四边形的有向面积；

 （2）叉积可以判断2 个 向量的转向关系(顺时针或逆时针)；

         （3）对于点集，叉积可以判断点的位置关系；

          （4）线段求交(两两横跨或某个点落在线段上) ，凸包求解;

3. 与叉乘区别

   两个向量叉乘得到一个垂直于这两个它们的向量;