隐马尔科夫学习（HMM）

最新推荐文章于 2020-07-28 11:33:59 发布

z6491679

最新推荐文章于 2020-07-28 11:33:59 发布

阅读量678

点赞数

分类专栏：算法

本文链接：https://blog.csdn.net/z6491679/article/details/50898135

版权

算法专栏收录该内容

18 篇文章 0 订阅

订阅专栏

一、简介

隐马尔科夫比马尔科夫多的一个东西就是随机变量不止一个了，而是分为了多个随机变量：
1、观测变量Ot：此变量仅由St决定，即仅有当前状态决定。
2、隐变量St:此变量满足马尔科夫性，可能有多个。
那么由此多了混淆矩阵（Confusion Matrix）：即P（St -> Ot）,就是隐状态到观测状态转移矩阵。其他的如初始状态，状态转移矩阵和马尔科夫一样。

二、3个问题

1、评估问题。
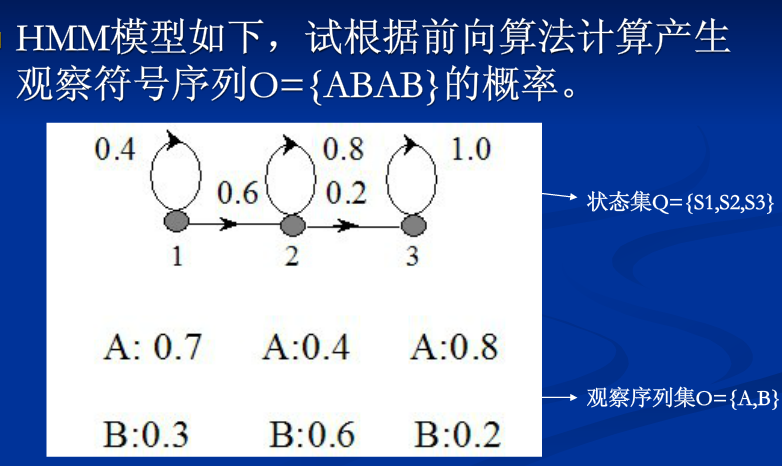
　　给定模型参数λ=(A,B,π)，求其生成观测序列 O=O1O2O3…Ot的概率，用前向算法即可。
这里写图片描述

#include <iostream>
using namespace std;

#define A 0
#define B 1
#define S_N 3
#define ZZMAX 100
#define O_N 2
float a[S_N][O_N] = { 0.7, 0.3,
                  0.4, 0.6, 
                  0.8, 0.2 };
float b[S_N][S_N] = { 0.4, 0.6, 0,
                  0, 0.8, 0.2,
                  0, 0, 1 };

int main()
{
    int seq_n = 4;
    int test[] = { A,B,A,B };
    float mid_res[S_N][ZZMAX];
    //初始化，即初始状态
    mid_res[0][0] = 0.7;
    mid_res[1][0] = 0;
    mid_res[2][0] = 0;
    //迭代，对每一个时间t计算每一个状态的可能性
    for (int i = 1; i < seq_n; i++)
    {
        for (int j = 0; j < S_N; j++)
        {
            float temp = 0;
            for (int k = 0; k < S_N; k++)
                temp += mid_res[k][i - 1] * b[k][j] * a[j][test[i]];
            mid_res[j][i] = temp;
        }
    }
    //累加结果
    float res = 0;
    for (int i = 0; i < S_N; i++)
        res += mid_res[i][seq_n - 1];
    cout << res << endl;
}

2.解码问题
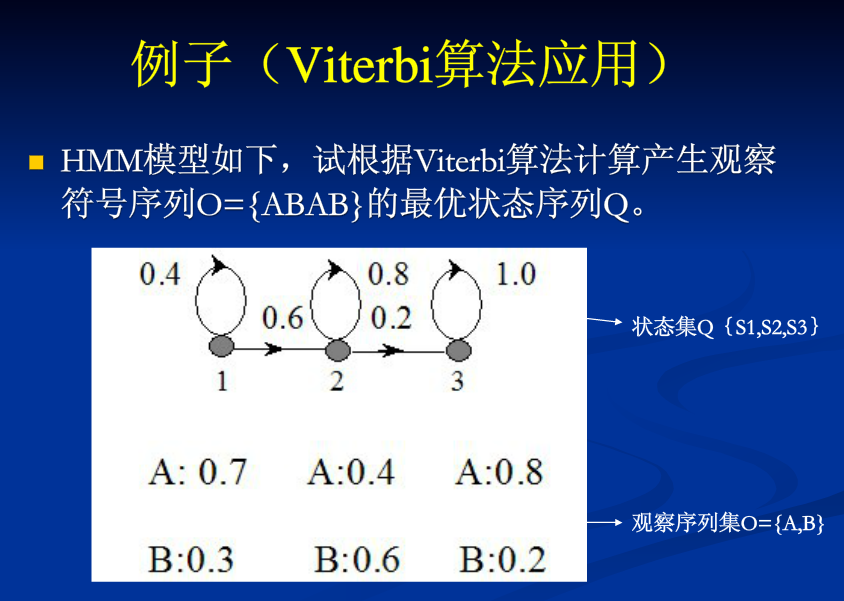
　　　给定模型参数λ=(A,B,π)和观测序列 O=O1O2O3…Ot，求最可能的隐状态序列Ｓ= S1S2S3…….St。用VIterbi算法　

这里写图片描述

#include <iostream>

using namespace std;


#define A 0
#define B 1
#define S_N 3
#define ZZMAX 100
#define O_N 2
float a[S_N][O_N] = { 0.7, 0.3,
                  0.4, 0.6, 
                  0.8, 0.2 };
float b[S_N][S_N] = { 0.4, 0.6, 0,
                  0, 0.8, 0.2,
                  0, 0, 1 };


int main()
{
    int seq_n = 4;
    int test[] = { A,B,A,B };
    float mid_res[S_N][ZZMAX];
    //记录维特比变量，即在t时刻取得最大概率的隐状态
    int Viterbi_var[100];
    //初始化
    mid_res[0][0] = 0.7;
    mid_res[1][0] = 0;
    mid_res[2][0] = 0;

    Viterbi_var[0] = 0;
    //迭代
    for (int i = 1; i < seq_n; i++)
    {
        float max_pro = 0;
        int temp_var;
        for (int j = 0; j < S_N; j++)
        {
            float temp = 0;
            for (int k = 0; k < S_N; k++)
                temp += mid_res[k][i - 1] * b[k][j] * a[j][test[i]];
            mid_res[j][i] = temp;
            if (max_pro < temp)
            {
                max_pro = temp;
                temp_var = j;
            }
        }
        Viterbi_var[i] = temp_var;
    }
    //Viterbi result，倒叙输出即可
    for (int i = 0; i < seq_n; i++)
        cout << Viterbi_var[i] << endl;
}

一个关于解码问题有趣的现实例子

1.题目背景：
从前有个村儿，村里的人的身体情况只有两种可能：健康或者发烧。
假设这个村儿的人没有体温计或者百度这种神奇东西，他唯一判断他身体情况的途径就是到村头我的偶像金正月的小诊所询问。
月儿通过询问村民的感觉，判断她的病情，再假设村民只会回答正常、头晕或冷。
有一天村里奥巴驴就去月儿那去询问了。
第一天她告诉月儿她感觉正常。
第二天她告诉月儿感觉有点冷。
第三天她告诉月儿感觉有点头晕。
那么问题来了，月儿如何根据阿驴的描述的情况，推断出这三天中阿驴的一个身体状态呢?
为此月儿上百度搜 google ，一番狂搜，发现维特比算法正好能解决这个问题。月儿乐了。

2.已知情况：
//S集合
隐含的身体状态 = { 健康 , 发烧 }

//O集合
可观察的感觉状态 = { 正常 , 冷 , 头晕 }

//初始状态
月儿预判的阿驴身体状态的概率分布 = { 健康：0.6 , 发烧： 0.4 }

//隐状态状态转移矩阵
月儿认为的阿驴身体健康状态的转换概率分布 = {
健康->健康： 0.7 ,
健康->发烧： 0.3 ,
发烧->健康：0.4 ,
发烧->发烧： 0.6
}

//混淆矩阵，即隐状态转移到观测状态转移矩阵
月儿认为的在相应健康状况条件下，阿驴的感觉的概率分布 = {
健康，正常：0.5 ，冷：0.4 ，头晕： 0.1 ；
发烧，正常：0.1 ，冷：0.3 ，头晕： 0.6
}

//观测序列
阿驴连续三天的身体感觉依次是：正常、冷、头晕。

3.题目：
已知如上，求：阿驴这三天的身体健康状态变化的过程是怎么样的？即求解最可能的隐状态序列

4.过程：
根据 Viterbi 理论，后一天的状态会依赖前一天的状态和当前的可观察的状态。那么只要根据第一天的正常状态依次推算找出到达第三天头晕状态的最大的概率，就可以知道这三天的身体变化情况。

1.初始情况：
P(健康) = 0.6，P(发烧)=0.4。

2.求第一天的身体情况：
计算在阿驴感觉正常的情况下最可能的身体状态。
P(今天健康) = P(正常|健康)P(健康|初始情况) = 0.5 0.6 = 0.3
P(今天发烧) = P(正常|发烧)P(发烧|初始情况) = 0.1 0.4 = 0.04
那么就可以认为第一天最可能的身体状态是：健康。