一、二维Gabor函数的规范化表示
网上关于二维Gabor函数的数学表达式各种各样,符号和形式不尽相同,其中不少表述非常不严谨。这里,在前两篇的理论基础上重新对Gabor函数的数学表达式进行整理,梳理其中各参数的数学含义,方便大家编写程序。
(1)表示方式一
其中,u是x方向的中心频率
v是y方向的中心频率





基于这一种表示方式,watkins在博客《gabor滤波器的几种实现方式》中做了进一步的扩展,即“方式三”描述的表示方式:




表示方式一的程序可以参考watkins的博客《gabor滤波器的几种实现方式》。
(2)表示方式二
此数学表达式为复数表达式:
实数部分:
虚数部分:
其中:
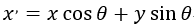
实际编程中一般使用的是实数部分,各个参数的具体含义和作用请参考《Gabor filter for image processing and computer vision》和它的中文翻译《Gabor滤波器学习》,或者博士学位论文《视觉显著性模型研究及其在影像处理中的应用》中的第四章。
二、Gabor函数的Matlab实现
新建一个名为CreatGabor.m的函数文件
function gaborValue = CreatGabor(x,y,lambda,theta,phi,gamma,b,varargin)
% CREATGABOR Produce a one-dimensional or two-dimensional Gabor kernal.
% [GABORKERNAL,VARARGOUT] =
% CREATGABOR(X,Y,LAMBDA,THETA,PHI,GAMMA,B,VARARGIN) generate a Gabor value
% according to the input arguments.
%
% Parameter options:
% -------------------
% x 对应Gabor函数值产生点的横坐标
% y 对应Gabor函数值产生点的纵坐标
% lambda 波长:值以像素为单位指定,通常大于等于2.但不能大于输入图像尺寸的五分之一
% theta 方向角:指定Gabor函数并行条纹的方向,取值为0到2*pi
% phi 相位移:取值范围为-pi度到pi,0和180度分别对应中心对称的center-on函数和center-off函数,而-pi/2和pi/2对应反对称函数
% gamma 方向曲率:亦称空间纵横比,决定Gabor函数形状(support,此处翻译为形状)的椭圆率(ellipticity),
% 当gamma = 1时,形状是圆的;当gamma < 1时,形状随着平行条纹方向而拉长。通常该值为0.5
% b Gabor滤波器的半响应空间频率带宽b和sigma/lambda的比率有关,其中sigma表示Gabor函数高斯因子的标准差
%
% written by Shane 2014-05-21 version1.0
x1 = x * cos(theta) + y * sin(theta);
y1 = y * cos(theta) - x * sin(theta);
sigma = lambda * ((2^b + 1) / (2^b - 1)) * (sqrt(log(2) / 2) / pi);
gaborValue = exp(- (x1^2 + gamma^2 * y1^2) / (2 * sigma^2)) * cos(2 * pi * x1 /lambda + phi);三、Gabor滤波器的具体应用
这里利用Gabor金字塔获取视觉显著想模型中的方向特征图,首先使用Gabor滤波器处理平均金字塔的每一层图像,从而得到Gabor金字塔,通过对Gabor金字塔的第三层双线性插值放大为到原图像大小,然后再用其减去Gabor金字塔的第一层图像,对相减之后的结果取绝对值,最后进行标准化得到的图像便是视觉显著性模型中的方向显著图。
程序如下:
%本程序使用Matlab2013b编写
close all;clear all;clc;
imInfo = imfinfo('2.jpg');
imObj = imread('2.jpg');
imGray = rgb2gray(imObj);
imGray = im2double(imGray);
%******************生成Gabor模板******************%
lambda = 2;theta = 0;phi = 0;gamma = 1;
sigma = 1; %理论上应该使用带宽b和波长lambda计算sigma的值,这里为了便于调试,直接定义sigma的值
M = 7;N = 7;R = 10;
[X,Y] = meshgrid(linspace(-R,R,N),linspace(-R,R,M));
X1 = X .* cos(theta) + Y .* sin(theta);
Y1 = Y .* cos(theta) + X .* sin(theta);
gaborKernal = exp(- (X1.^2 + gamma^2 .* Y1.^2) ./ (2 * sigma^2)) .* cos(2 .* pi .* X1 ./lambda + phi);
%******************标准化Gabor模板******************%
gaborKernalSum = sum(gaborKernal(:));
gaborKernalSum = gaborKernalSum / (M * N);
gaborNormalKernal = gaborKernal - gaborKernalSum;
%******************生成L层高斯金字塔******************%
% L = 5; %定义金字塔层数
% gaussPyrLevel = cell(L);
% gaussKernal = fspecial('gaussian',[5 5],1);
% gaussPyrLevel{1} = imfilter(imGray,gaussKernal,'symmetric','same','conv'); %高斯金字塔基图像(第0级图像)
% rowSample = downsample(gaussPyrLevel{1},2);
% columnSample = downsample(rowSample',2);
% gaussPyrLevel{2} = columnSample';
% for i = 3 : L
% levelTemp = imfilter(gaussPyrLevel{i - 1},gaussKernal,'symmetric','same','conv');
% rowSample = downsample(levelTemp,2);
% columnSample = downsample(rowSample',2);
% gaussPyrLevel{i} = columnSample';
% end
%******************生成L层平均金字塔******************%
L = 5;
avePyrLevel = cell(L);
avePyrLevel{1} = imGray;
for k = 2 : L
[m,n] = size(avePyrLevel{k - 1});
m = floor(m / 2);n = floor(n / 2);
avePyrLevel{k} = zeros(m,n);
for i = 1 : m %计算大小为2*2的网格内的像素均值
for j = 1 : n
avePyrLevel{k}(i,j) = (avePyrLevel{k - 1}(i * 2,j * 2) + avePyrLevel{k - 1}(i * 2,j * 2 - 1) ...
+ avePyrLevel{k - 1}(i * 2 - 1,j * 2) + avePyrLevel{k - 1}(i * 2 - 1,j * 2 - 1)) / 4;
end
end
end
%******************生成L层Gabor金字塔******************%
gaborPyrLevel = cell(L);
for i = 1 : L
gaborPyrLevel{i} = imfilter(avePyrLevel{i},gaborNormalKernal,'symmetric','same','conv');
end
%******************生成方向特征图******************%
gaborPyrLevelZoom = imresize(gaborPyrLevel{3},[imInfo.Height imInfo.Width],'bilinear');
dirFeature = abs(gaborPyrLevelZoom - gaborPyrLevel{1});
%******************标准化方向特征图******************%
dirFeatureSum = sum(dirFeature(:));
dirFeatureSum = dirFeatureSum / (imInfo.Height * imInfo.Width);
dirFeature =dirFeature - dirFeatureSum;
%******************将取值区间移到[0,1]内,方便显示******************%
valMax = max(gaborNormalKernal(:));
valMin = min(gaborNormalKernal(:));
gaborNormalKernal = (gaborNormalKernal - valMin) ./ (valMax - valMin);
for i = 1 : 5
valMax = max(gaborPyrLevel{i}(:));
valMin = min(gaborPyrLevel{i}(:));
gaborPyrLevel{i} = (gaborPyrLevel{i} - valMin) ./ (valMax - valMin);
end
valMax = max(dirFeature(:));
valMin = min(dirFeature(:));
dirFeature = (dirFeature - valMin) ./ (valMax - valMin);
%******************显示图像******************%
display(gaborKernal);
figure('Name','Gabor调试过程','NumberTitle','off');
subplot(3,4,1);subimage(imObj);
title('原始图像');
for i = 1 : 5
subplot(3,4,1 + i);subimage(avePyrLevel{i});
title(strcat('avePyrLevel{',num2str(i),'}'));
end
for i = 1 : 5
subplot(3,4,6 + i);subimage(gaborPyrLevel{i});
title(strcat('gaborPyrLevel{',num2str(i),'}'));
end
subplot(3,4,12);subimage(dirFeature);
title('方向特征图');
处理结果如下图所示:
处理结果一般是因为为了说明原理,参数设置只取了常用的值,并没有细致地调整参数,如果参考这篇博文,请根据源程序自己结合需求对参数进行调节。
至此,关于Gabor金字塔在视觉注意模型中的应用的介绍就结束了,这当中着重对Gabor变换进行了描述,因为我们这里旨在将Gabor变换讲明白,应用在其次,应古人那句话“授人以鱼不如授人以渔”。当然这三篇文章中难免有错误和疏漏之处,希望高手不吝赐教,批评指正。








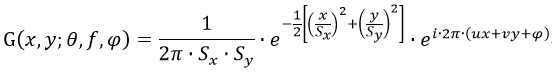

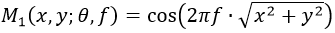

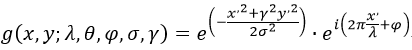
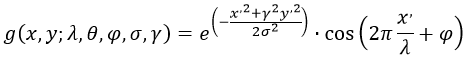
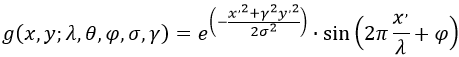

















 8360
8360

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








