水流波动的波形都是三角波,曲线是正余弦曲线,但是Android中没有提供绘制正余弦曲线的API,好在Path类有个绘制贝塞尔曲线的方法quadTo,绘制出来的是2阶的贝塞尔曲线,要想实现波动效果,只能用它来绘制Path曲线。待会儿再讲解2阶的贝塞尔曲线是怎么回事,先来看实现的效果:
这个波长比较短,还看不到起伏,只是荡漾,把波长拉长再看一下:
已经可以看到起伏很明显了,再拉长看一下:
这个的起伏感就比较强了。利用这个波动效果,可以用在绘制水位线的时候使用到,还可以做一个波动的进度条WaveUpProgress,比如这样:
是不是很动感?
那这样的波动效果是怎么做的呢?前面讲到的贝塞尔曲线到底是什么呢?下面一一讲解。想要用好贝塞尔曲线就得先理解它的表达式,为了形象描述,我从网上盗了些动图。
首先看1阶贝塞尔曲线的表达式:
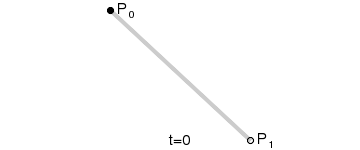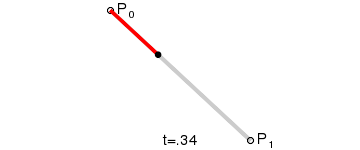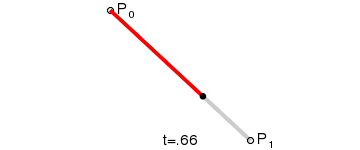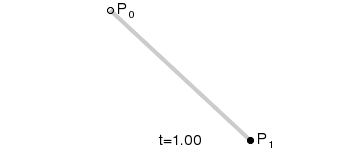
随着t的变化,它实际是一条P0到P1的直线段:
Android中Path的quadTo是3点的2阶贝塞尔曲线,那么2阶的表达式是这样的:
看起来很复杂,我把它拆分开来看:
然后再合并成这样:
看到什么了吧?如果看不出来再替换成这样:
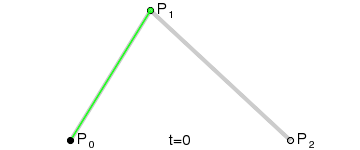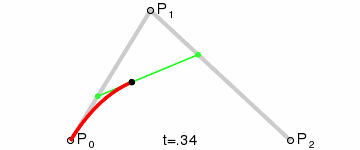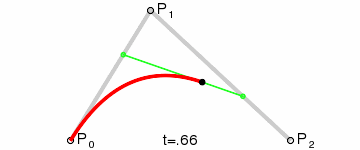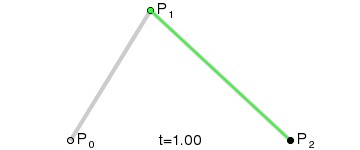
B0和B1分别是P0到P1和P1到P2的1阶贝塞尔曲线。而2阶贝塞尔曲线B就是B0到B1的1阶贝塞尔曲线。显然,它的动态图表示出来就不难理解了:
红色点的运动轨迹就是B的轨迹,这就是2阶贝塞尔曲线了。当P1位于P0和P2的垂直平分线上时,B就是开口向上或向下的抛物线了。而在WaveView中就是用的开口向上和向下的抛物线模拟水波。在Android里用Path的方法,首先path.moveTo(P0),然后path.quadTo(P1, P2),canvas.drawPath(path, paint)曲线就出来了,如果想要绘制多个贝塞尔曲线就不断的quadTo吧。
讲完贝塞尔曲线后就要开始讲水波动的效果是怎么来的了,首先要理解,机械波的传输就是通过介质的震动把波形往传输方向平移,每震动一个周期波形刚好平移一个波长,所有介质点又回到一个周期前的状态。所以要实现水波动效果只需要把波形平移就可以了。
那么WaveView的实现原理是这样的:
首先在View上根据View宽计算可以容纳几个完整波形,不够一个的算一个,然后在View的不可见处预留一个完整的波形;然后波动开始的时候将所有点同时在x方向上移动相同的距离,这样隐藏的波形就会被平移出来,当平移距离达到一个波长时,这时候将所有点的x坐标又恢复到平移前的值,这样就可以一个波形一个波形地往外传输。用草图表示如下:
WaveView的原理在上图很直观的看出来了,P[2n+1],n>=0都是贝塞尔曲线的控制点,红线为水位线。
波浪效果
波浪的绘制是贝塞尔曲线一个非常简单的应用,而让波浪进行波动,其实并不需要对控制点进行改变,而是可以通过位移来实现,这里我们是借助贝塞尔曲线来实现波浪的绘制效果,效果如图所示:

package com.xys.animationart.views;
import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.util.AttributeSet;
import android.view.View;
import android.view.animation.LinearInterpolator;
/**
* 波浪图形
*/
public class WaveBezier extends View implements View.OnClickListener {
private Paint mPaint;
private Path mPath;
private int mWaveLength = 1000;
private int mOffset;
private int mScreenHeight;
private int mScreenWidth;
private int mWaveCount;
private int mCenterY;
public WaveBezier(Context context) {
super(context);
}
public WaveBezier(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
}
public WaveBezier(Context context, AttributeSet attrs) {
super(context, attrs);
mPath = new Path();
mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mPaint.setColor(Color.LTGRAY);
mPaint.setStyle(Paint.Style.FILL_AND_STROKE);
setOnClickListener(this);
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
mScreenHeight = h;
mScreenWidth = w;
mWaveCount = (int) Math.round(mScreenWidth / mWaveLength + 1.5);
mCenterY = mScreenHeight / 2;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPath.reset();
mPath.moveTo(-mWaveLength + mOffset, mCenterY);
for (int i = 0; i < mWaveCount; i++) {
// + (i * mWaveLength)
// + mOffset
mPath.quadTo((-mWaveLength * 3 / 4) + (i * mWaveLength) + mOffset, mCenterY + 60, (-mWaveLength / 2) + (i * mWaveLength) + mOffset, mCenterY);
mPath.quadTo((-mWaveLength / 4) + (i * mWaveLength) + mOffset, mCenterY - 60, i * mWaveLength + mOffset, mCenterY);
}
mPath.lineTo(mScreenWidth, mScreenHeight);
mPath.lineTo(0, mScreenHeight);
mPath.close();
canvas.drawPath(mPath, mPaint);
}
@Override
public void onClick(View view) {
ValueAnimator animator = ValueAnimator.ofInt(0, mWaveLength);
animator.setDuration(1000);
animator.setRepeatCount(ValueAnimator.INFINITE);
animator.setInterpolator(new LinearInterpolator());
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
mOffset = (int) animation.getAnimatedValue();
postInvalidate();
}
});
animator.start();
}
}












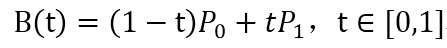
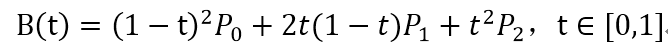
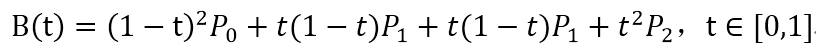
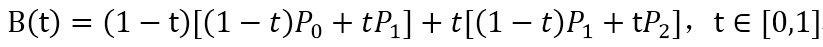
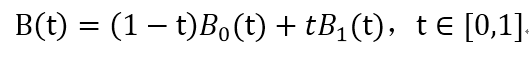
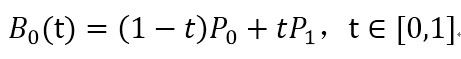
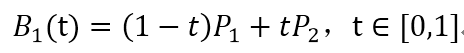

















 771
771

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








