算法 | 基础 - [常见问题]

小和问题

问题说明：
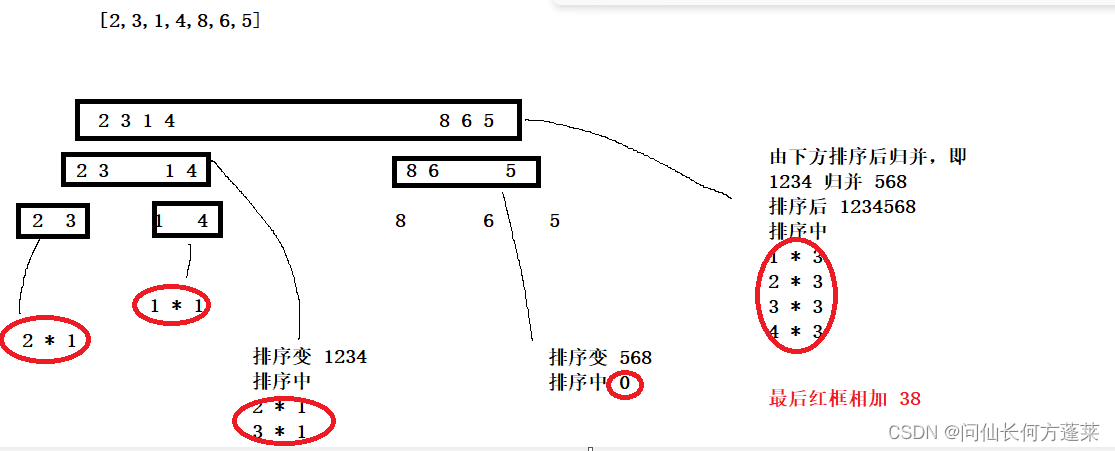
若某数组 [2,3,1,4,8,6,5]，分别计算每个元素左侧比它小的数字之和，在将这些和求和，即小和，
例子中为 0+2+0+6+10+10+10 = 38
思路：
转换为：计算元素右侧比它大的元素的个数的加权和
即：${\sum }_0^{length-1}(arr[i]\ast coun{t}_{big})$
例子中为 2 * 5 + 3 * 4 + 1 * 4 + 4 * 3 + 8 * 0 +6 * 0 + 5 * 0 = 38
结合归并排序，示意图如下
排序可以方便的比较比某元素大或小的个数（计算索引就行）
归并可以使上一级归并复用下一级归并的统计结果
PS：归并遇到两侧相等时，优先归并右侧，否则无法准确记录个数
如 [1,1,2,2] 与 [1,1,1,3,4]，优先归并左侧会变为 [1,1,2,2] 与 [1,1,1,3,4]
此时，不能通过索引计算统计大于个数左侧元素的个数

复杂度： $O(n\ast \log n)$，$O(n)$
套用 master ：$T(n)=2\ast (n/2)+O(n)$

逆数对问题

若某数组 [2,3,1,4,8,6,5]，左侧数比右侧大，则构成逆数对，统计逆数对的个数
如 2,1、3,1、8,6、8,5、6,5
思路：使用归并排序（反序），可以快速统计右侧小于左侧的元素数量，每个数量使逆序对数量 + 1
注意：左右一样先排右侧，否则不能准确统计个数

几乎有序数组排序问题

几乎有序的数组：每个元素举例它们排序后位置不超
过 k
以 k=6 为例

• 转化数组前 k + 1 = 7 个元素为小根堆
  因为 7 以后的元素不可能调整到 0 上
• 小根堆中移除 0 ，增加数组的下一个元素，以此类推
  复杂度： $O(n)$，$O(1)$
  因为堆相对于数组可以忽略不计，所以 heapify、heap insert 的负载度可以认为是 $O(1)$
  每个元素执行一轮，因此是 $O(n)$

反转链表

注意 若反转链表后要求 head 符合反转后的情况，需要设置返回值，返回新的 head

回文链表

如 [1,2,3,2,1] 或 [2,3,1,1,3,2] 类似的单向链表
压栈法，$O(n)$，$O(n)$
改序法，$O(n)$，$O(1)$

• 记录头结点
• 使用快慢指针找到中点位置
• 从中点向尾遍历，中点指向 null，获取 next 和 next 的 next 后，next指针指向当前
• 遍历至结束，记录尾结点位置
• 头尾节点向中间遍历，比较节点，不一样就不是
• 遍历的同时，从原尾开始还原链表

按基准值整理链表

对单向链表，取一个基准值，小的放左边，等于放中间，大于放右边，元素相对顺序不变，要求 $O(n)$
数组法，$O(n)$，$O(n)$
链表改数组然后归并排序然后还原
区域指针法，$O(n)$，$O(1)$

• 准备一个数组 p[6]，元素分别为小中大于区的头尾指针
• 遍历节点，放入对应的区
  • 首次放入时，此区域头尾指针都指向此节点（因此，一个区域要不收尾指针都有，要不都没有）
  • 其余放入时，区域尾结点的 next 指向此节点，此节点变为新的尾
• 整理指针，以串联三个区域的边界，但需要考虑区域缺失的问题
  • 从左到右串联指针数组
  • 跳过 null
  • 跳过 01、23、45 之间的串联，因为是区域内

有随机指针的单向链表复制

单向链表，要求复制此链表，其节点结构如下

Class Node<V>{
	V value;
	Node next;
	Node random;
}

random 指针可能指向链表中任意节点，或指向 null

Map 法，$O(n)$，$O(n)$
原节点和它的复制节点作为键值对存 map，然后遍历设置
原地克隆法，$O(n)$，$O(1)$

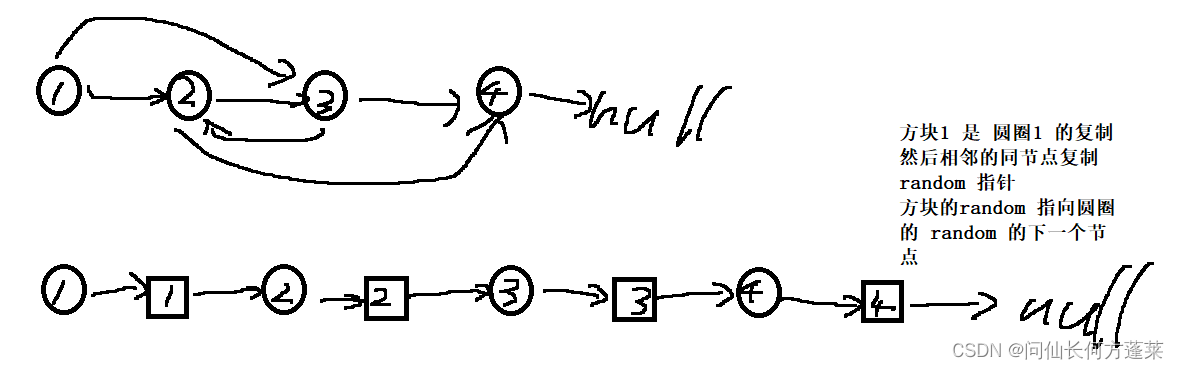
• 一次克隆每个节点，新节点挂在原节点之后
• 两两节点一组，遍历复制 random 指针
  复制节点的 random 指向原节点 random 所指节点的下一个节点
• 删除原节点，返回头
  

链表成环

单向链表是否有环，如果有返回入环第一个节点

Hash 法，$O(n)$，$O(n)$
遍历链表，每遍历一格节点先检查是否存在于 Hash，若不存在就存入 Hash，若遍历完之前检查到存在，就有环
被检查到的节点就是入环节点
快慢指针法，$O(n)$，$O(1)$

• 两个指针，一快一慢，慢指针每次走一格，快指针每次走两格
• 若两指针再次相遇就是有环
• 重合后，快指针回到 head，快慢指针都走一格
• 再次重合，指向的节点就是第一个入环节点

两条链表相交

两条单向链表，可能有环，可能没环，判断是否相交，如果重合，返回重合的第一个节点

解法如下，需要分步骤分情况套路，$O(n)$，$O(1)$

• 先判断两条链表分别是否有环
• 如果无环
  • 分别遍历两条链表，记录长度与 tail
  • 判断两个 tail 是否是同一个节点，是则相交，否则不相交
  • 如果相交，两链表都从 head 开始遍历，但较长的链表先遍历 两链表长度之差 格
  • 继续遍历，一次一格，相遇即是相交第一个元素
    
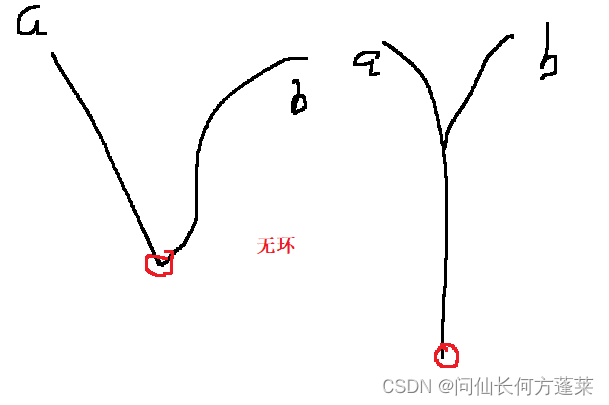
• 如果一个有环一个无环
  不存在，如下图所示，红圈处节点不可能存在于单链表
  
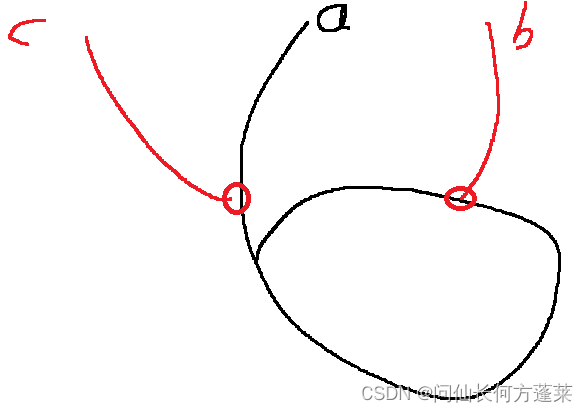
• 都有环
  • 分如下图三种情况，两环独立、共用入环节点、不共用入环节点
    
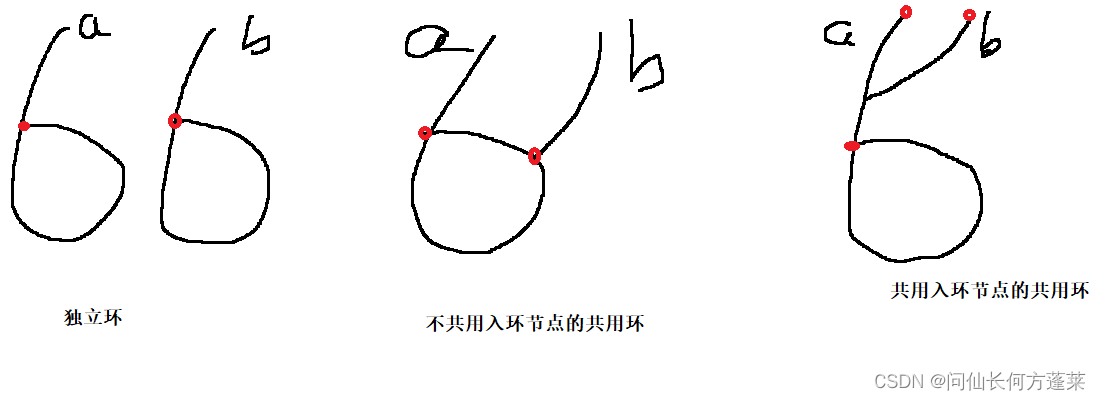
  • 比较两个链表的入环点
    • 若两个链表入环点相同，说明是 共用入环节点 情况
    • 若两个链表入环点不同，从任意一个入环点向下遍历，先遇到自己，说明是 两环独立 情况
    • 若两个链表入环点不同，从任意一个入环点向下遍历，先遇到另一个入环点，说明是 不共用入环节点 情况
  • 两环独立时，即 不相交，返回 null
  • 共用入环节点 时，两链表 相交
    • 取共用的入环节点为两个链表共同的尾，两个链表的头为分别的头
    • 其余流程同 两链表都无环，如上图最右侧红点处
  • 不共用入环节点 时，两链表 相交，返回 任意一个入环点 都符合要求

二叉树的递归遍历

二叉树的递归遍历类似下面伪代码

scanNode(node){
	if(node == null) return;
	//1
	scanNode(node.left);
	//2
	scanNode(node.right);
	//3
}

注意，// 1 ~ 3 处都会回到对 当前节点 的遍历逻辑
下面的三种递归顺序分别对应在 // 1 ~ 3 处输出自己

根据遍历每一个节点自身 (或称：头) 和 左右子树 的顺序衍生出三种递归遍历

• 先序遍历
  对每个节点，按 头、左子树、右子树 的顺序遍历
• 中序遍历
  对每个节点，按 左子树、头、右子树 的顺序遍历
• 后序遍历
  对每个节点，按 左子树、右子树、头 的顺序遍历

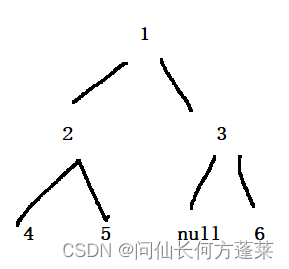
二叉树的栈遍历

二叉树的栈遍历类似下面伪代码
前序 (同时也是宽度遍历)

stack.add(root);
while(!stack.isEmpty()){
	curr == stack.pop();
	if(curr== null) return;
	//1
	if(curr.right != null)
		stack.push(curr.right);
	if(curr.left != null)
		stack.push(curr.left);
}

流程

• 先将 root 压栈
• 开始循环
  • 只要栈里还有元素，就不退出循环
  • 弹出栈顶
  • 如果有右孩子，右孩子压栈
  • 如果有左孩子，做孩子压栈
  • // 1 处打印 curr
  • 重复

后序

stack.add(root);
while(!stack.isEmpty()){
	curr == stack.pop();
	stack2.push(curr);
	if(curr== null) return;
	if(curr.right != null)
		stack.push(curr.right);
	if(curr.left != null)
		stack.push(curr.left);
}
while(!stack2.isEmpty())
	print(stack2.pop());

流程

• 先将 root 压第一个栈
• 开始循环第一个栈
  • 只要栈里还有元素，就不退出循环
  • 弹出栈顶，压入第二个栈
  • 如果有右孩子，右孩子压栈
  • 如果有左孩子，做孩子压栈
  • 重复
• 遍历第二个栈，顺次打印

中序

while(!stack.isEmpty() || curr != null){
	if(curr!= null){
		stack.push(curr);
		curr = curr.left;
	}else{
		curr = stack.pop();
		print(curr);
		curr = curr.right;
	}
}

流程

• 先将 root 压第一个栈
• 开始循环第一个栈
  • 只要栈里还有元素，就不退出循环
  • 弹出栈顶，压入第二个栈
  • 如果有右孩子，右孩子压栈
  • 如果有左孩子，做孩子压栈
  • 重复
• 遍历第二个栈，顺次打印

二叉树宽度优先遍历

即按层遍历，先遍历第一层，然后第二层、第三层

队列法

• 根节点进队列
• 循环，只要队列里有值，就不退出循环
• 取出队列中的头
• 打印头
• 如果头有孩子，头的左孩子、右孩子依次进队列
• 重复

queue.add(root);
while(!queue.isEmpty()){
	curr == queue.poll();
	queue.add(curr.left);
	queue.add(curr.right);
}

二叉树的序列化

• 同各种遍历
• null 使用 # 表示
• 使用 _ 连接各个节点值

String serial2String(node){
	if(null==node)
		return "#_";
	String serial = node.value + "_";
	serial += serial2String(node.left);
	serial += serial2String(node.right);
	return serial ;
}

二叉树的反序列化

按序重建二叉树

• 按 _ 拆分字符串为数组
• 重建顺序同二叉树遍历顺序
• 遇到 # 表示轮到的需要创建的节点为 null

queue split2queue(str){
	string[] nodes = str.split("_");
	queue<String> queue = new LinkedList<String>();
	for(string node:nodes){
		queue.add(node);
	}
}
node deserial(queue){
	str = queue.poll();
	if(str.equals("#"))
		return null;
	node = new Node(str);
	node.left = deserial(queue);
	node.right = deserial(queue);
	return node;
}

二叉树的最大宽度

map 法，$O(n)$，$O(n)$

map;
currLevel,currLevelNodeCount;
maxLevel,maxLevelNodeCount;
queue.add(root);
while(!queue.isEmpty()){
	curr == queue.poll();
	if(map.get(curr)==currLevel){
		currLevelNodeCount++;
	}else{
		if(currLevelNodeCount > maxLevelNodeCount){
			maxLevel = currLevel;
			maxLevelNodeCount = currLevelNodeCount;
		}
		currLevel++;
		currLevelNodeCount = 1;
	}
	if(curr.left != null){
		map.put(curr.left,currLevel+1);
		queue.add(curr.left );
	}
	if(curr.right != null){
		map.put(curr.right,currLevel+1);
		queue.add(curr.right );
	}
}

流程

• 准备一个 map ，存节点和它层数的映射
• 准备遍历存储当前层数、当前层节点数、历史最多节点最多的层和节点数
• 先将 root 放入队列
• 开始循环
  • 只要队列里还有元素，就不退出循环
  • 取出队列中第一个节点
  • 是当前层，层节点 +1；否则统计当前层数量与历史比对，且层数 +1
  • 如果有左孩子，左孩子进队列，存入map
  • 如果有右孩子，右孩子进队列，存入map
  • 重复

队列节点标记法，$O(n)$，$O(1)$
流程

• 准备两个 node，为 当前层尾节点(ct)、下一层尾节点(nt)
• 准备一个 int count，max，为当前层节点数量、最大层节点数量；
• 先将 root 放入队列，ct = root
• 开始循环
  • 只要队列里还有元素，就不退出循环
  • 取出队列中第一个节点，count++
  • 如果有左孩子，左孩子进队列，nt = left
  • 如果有右孩子，右孩子进队列，nt = right
  • 当前节点是否是 ct，是就结算，比较count和max
  • ct = nt，nt = null，count = 0
  • 重复

二叉树题目(二叉树动态规划)通用思路

• 思考完成题目的条件
• 确定需要向左右子树索要哪些信息
• 递归完成

示例见 判断是否是平衡二叉树

最近共同祖先节点

node1，node2 在树中，求其最近共同祖先节点

补完全二叉树法
将数按宽度遍历，null也进入数组，弹出节点的操作用指针模拟，
遇到 null 认为是节点，加入数组，弹出 null 后认为其有两个节点都是 null，也加入数组
遇到 node1，node2 时，额外记录位置
直到把 node1，node2 放入数组，认为树补充完

选择 node1，node2 中索引靠前的，通过 $(index-1)/2$ 找爹找爷爷找祖宗，存入 set
选择另一个，重复上一步过程，直到 set 里存在
（或从索引较大的开始找，每计算一步比较是否在另一个节点之前了，如果是换另一个节点计算，直到重合）

父节点 map 法
宽度遍历，遍历是记录和父节点的映射，直到 node1、node2都存入map
其他逻辑类似 补完全二叉树法

递归包含判断法
若某节点是 node1、node2 的最近共同祖先，满足下面场景之一

• 节点的左右子树，分别包括 node1、node2
• 节点的左右子树之一，和节点自身，分别包括 node1、node2
  因此递归所有节点，直到遇到第一个这样的节点

//考虑二者可能不在树中的情况
node origin(node,origin){
	if(origin!=null)//找到了
		return origin;
		
	if(node == null)//分支遍历到头了
		return null;//没有
	if(node == node1)//此分支包含 node1，下同理
		return node1;
	if(node == node2)
		return node2;

	left = origin(node.left);
	right = origin(node.right);

	if(left != null && right!=null){ //左右本别有俩目标的
		origin = node;
		return node;
	}
	if((left!=null || right!=null) && (node==node1 || node==node2)){ //自己本身就是祖宗的
		origin = node;
		return node;
	}

	//如果有值
	return left!=null?left:right;
}

后继节点

若某树节点上有指向父节点的指针，且指针都是对的，求某节点的后继节点
后继节点：按中序变量，某节点的后一个节点
前驱节点：按中序变量，某节点的前一个节点

• 若有右孩子
  • 右孩子有左孩子，返回右孩子的子树下最左的左孩子
  • 右孩子没有左孩子，返回右孩子（这是上一条的特例）
• 若没有右孩子
  • 若是父的左孩子，返回父（这是下一条的特例）
  • 若是父的右孩子，查找父的父级，直到某一级不是更上级的右孩子，更上级就是后继

node successor(node){
	if(null == node)
		return null;
	if(node.right != null){
		node = node.right;
		while(node.left != null)
			node = node.left;
		return node;
	}else{
		p = node.parent;
		while(parent!=null && parent.left!=node){
			node = p;
			p = node.parent;
		}
		return parent;
	}
}

判断搜索二叉树

做中序遍历，只要遍历过程中没有降序(包括相等节点)，记为搜索二叉树

判断完全二叉树

节点判断法
做宽度遍历，出现下面情况任意则不是完全二叉树

• 某节点没有左孩子但有右孩子
• 第一个有左无右的节点之后，任意节点不是叶子节点(无左无右)

null 节点信号法
做宽度遍历，弹栈时出现的第一个 null 后，不能出现其他非 null 的节点

递归判断法
递归二叉树，对任意节点满足下面条件

• 左树、右树都是搜索二叉树
• 左树的最大值 < 节点
• 节点 < 右树的最小值

判断满二叉树

数数法
宽度遍历，获取最大深度 d 与总元素个数 c，判断 $c=2^d-1$

判断平衡二叉树

对二叉树上任意节点，需要满足下列条件

• 左右子树都是平衡二叉树
• 左右子树的高度不能超过 1

class Result{
	private int d;
	private boolean bbt;
}
Result check(node){
	if(null==node)
		return new Result(true,0);
	
	Return left = check(node.left);
	Return right = check(node.right);

	int d = max(left.d,right.d)+1;
	boolean bbt = left.bbt && right.bbt && Math.abs(left.d -right.d) <2;
	return new Result(bbt,d);
}

折纸问题

一张纸，对折，记录折痕方向为 O；再对折，发现有反向折痕，记为 X，且所有折痕为 OOX
求：对折 n 次，所有折痕 顺序

分析，如下图，可见每次对折

• 会在上一次对折的折痕之外，产生两倍的新折痕
• 新折痕产生于上一次对折的新折痕两侧
• 两侧的新折痕，总是上端与老折痕一致，下端与老折痕相反

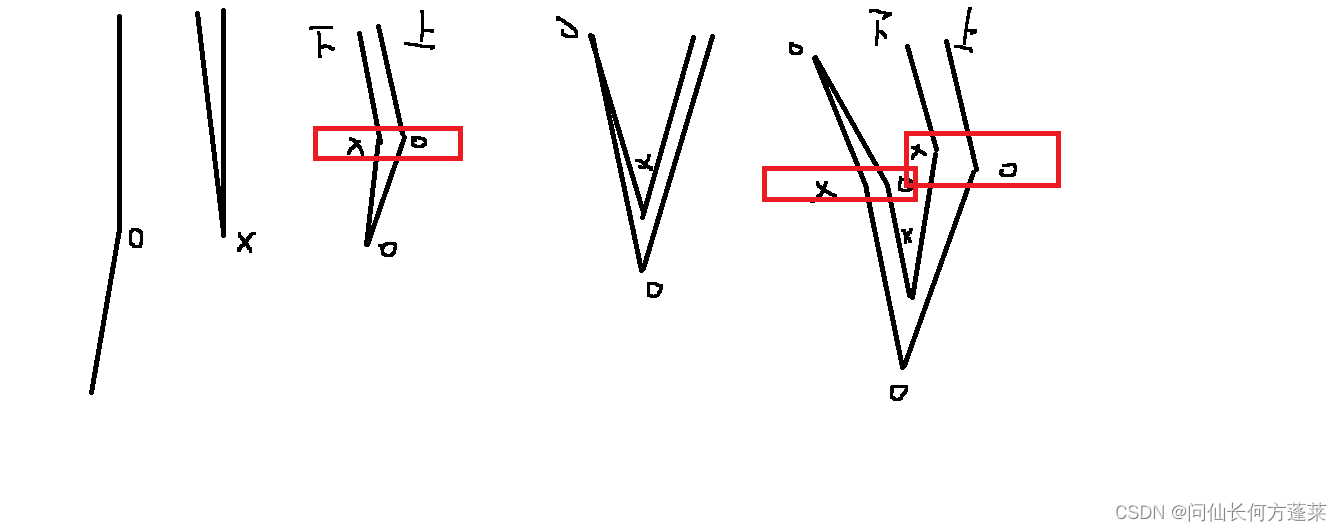
按上面归类整理可得

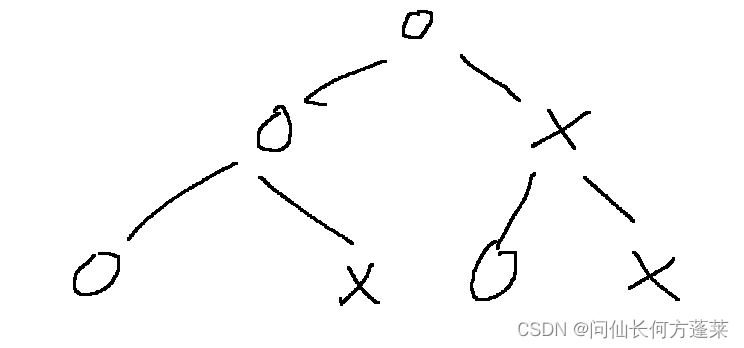
则所有折痕顺序为上图思路的 中序遍历

node = new Node("O");
// 用于生长这棵树，但并不必要
node group(node,n){
	if(n<0)
		return null;
	node.left = group(new node("O"),n-1);
	node.right = group(new node("X"),n-1);
	return node;
}

// 不用生长直接打印
printTree(node,n){
	if(n<0)
		return null;
	
	printTree("O",n-1);
	sout("node");// 整体保持中序遍历
	printTree("X",n-1);
}
// 用下面调用
printTree("O",n);

图表达方式的转化

若有如下二维数组，将其转化为 通用代码表达

{
	[2,4,5], // 0 表示从哪个顶点出发，1 表示连接到哪个顶点，2 表示边的权重
	[8,3,4],
	...
}

Graph createGraph(int[][] matrix){
	Graph g = new Graph();
	for(int[] arr: matrix){
		int from = arr[0];
		int to = arr[1];
		int weight = arr[2];
		if(!g.nodes.containsKey(from))
			g.nodes.put(from,new Node(from));
		if(!g.nodes.containsKey(to))
			g.nodes.put(to,new Node(to));
		
		Node fn = g.nodes.get(from);
		Node tn = g.nodes.get(to);

		Edge e = new Edge(weight,from,to);

		g.edges.add(e);
		fn.edges.add(e);
		fn.nexts.add(tn);
		fn.out++;
		tn.in++;
	}
	return g;
}

图的宽度优先遍历

因为图是很可能有环的，所以遍历的过程中需要查重机制

• 准备队列和 set
• 将一个顶点放入队列
• 开始循环，队列中只要还有顶点，就不退出循环
• 从队列中取顶点
• 打印顶点
• 将顶点的相邻节点，不在 set 中的部分加入队列，并在 set 中注册

图的深度优先遍历

因为是对图的遍历，所以栈里需要保存完整的遍历路径

• 准备栈和 set
• 将一个顶点放入栈
• 开始循环，栈中只要还有顶点，就不退出循环
• 从栈中弹出顶点
• 打印顶点
• 若顶点还有相邻顶点，拿到其中一个
• 如果新顶点在 set 里，拿原顶点的下一个相邻顶点
• 如果新顶点不在 set 里
  • 原顶点压回栈
  • 原顶点的当前相邻顶点压栈
  • 原顶点的当前相邻顶点加入 set
• break

图的拓扑排序

对项目进行编译，编译时需要将项目的依赖先行编译，项目的依赖又可能存在依赖关系
此时就是拓扑排序

• 找到图中入度为 0 的点 a，认为它是起点
• 打印 a
• 将 a 点与其影响擦掉
• 重复上面过程

List<Node> topology(Graph g){
	Map<Node,Integer> inMap = new HashMap();
	Queue<Node> zeros = new LinkedList<>();
	List<Node> sorted = new ArrayList();

	for(Node node : g.nodes.values()){
		inMap.put(node,node.in);
		if(node.in == 0) 
			zeros.add(node);
	}
	while(!zeros.isEmpty()){
		Node curr = zeros.poll();
		sorted.add(curr);
		inMap.remove(curr);
		for(Node n: curr.next){
			if(inMap.get(n)-1 == 0)
				zeros.add(n);
			
			inMap.put(n,inMap.get(n)-1);
		}
	}
	
	return sorted;
}

克鲁斯卡尔算法(kruskal)

用于计算网的 最小生成树
以边为切入点，适合边少的图

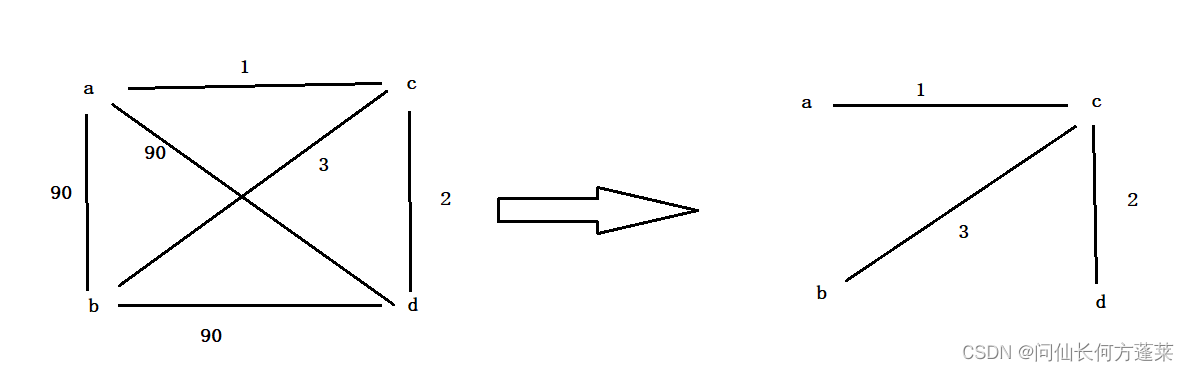
• 将所有的边按其权重排序
• 从最小的边开始添加
• 若加入某条边对导致形成环，丢弃这条边
• 直到所有边完成遍历

如何判断形成环

• 先使每个点单独存在各自的集合中
• 对任意一条边，检查边的两端是否在同一个集合
• 如果不在，可以添加边，并合并包含两个顶点的集合
• 如果在，丢弃边

如何实现形成环
并查集实现

其他实现

普里姆算法(prim)

用于计算网的 最小生成树，以点为切入点

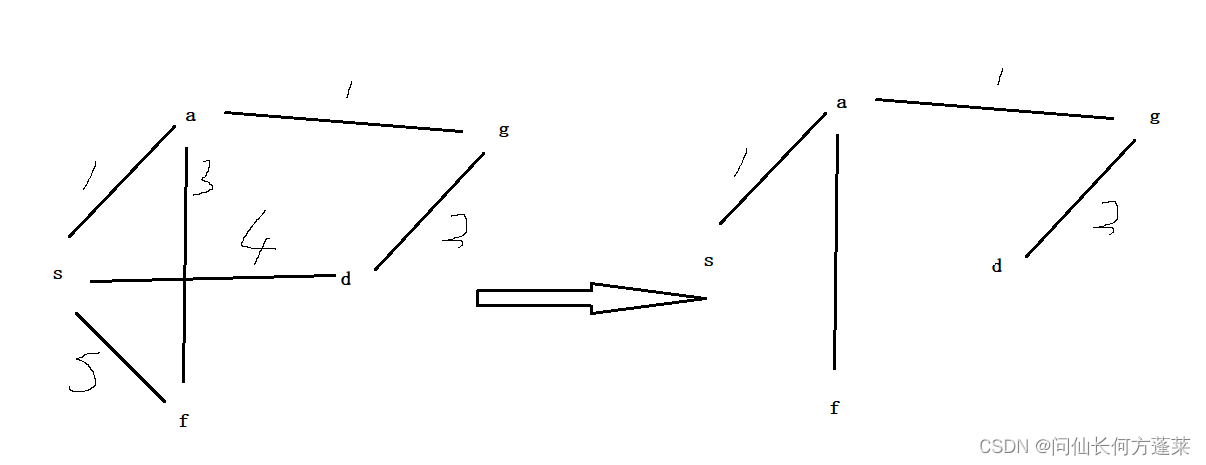
• 任选一个节点，加入结果
• 遍历此结果的所有边，将以前没有被激活的边标记为激活
• 选取刚刚激活的边中最小的，将另一个节点拉入结果
• 重复上面过程

Set<Node> tree = new HashSet();
Set<Edge> result = new HashSet();
PriorityQueue ae = new Priority<>(new EdgeComparator());

for(Node n: graph.nodes.values()){
	if(!tree.contains(n)){
		set.add(n);
		for(Edge e:n.edges())
			ae.add(e);
		while(!ae.isEmpty()){
			currMin = ae.poll();
			newNode = currMin.to;
			if(!tree.contains(newNode)){
				tree.add(newNode);
				result.add(e);
				for(Edge ne: newNode.edges)
					ae.add(ne);
			}
		}
	}
}

迪克斯特拉算法(Dijkstra)

用于计算网一个顶点到其他顶点的最短举例
要求网中不能存在 边权值累计为负数的环

如下图示例，从下图 a 出发

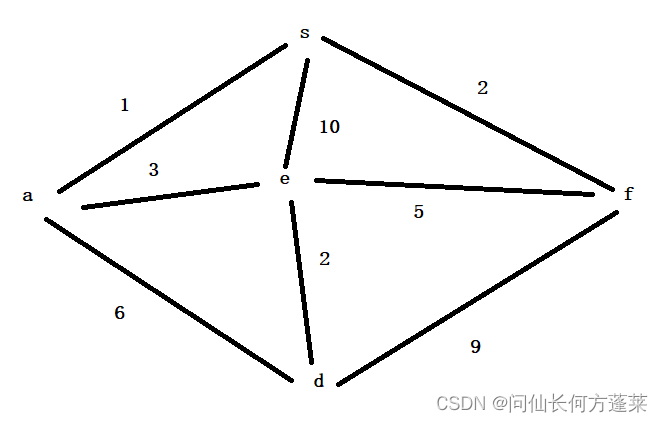
得到下表结论

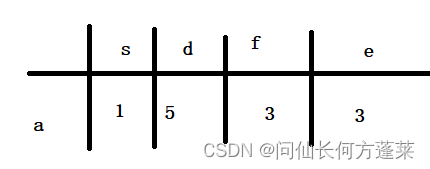
过程

• 先准备下图表，自己到自己长度 0 ，其他都认为是 ∞
  
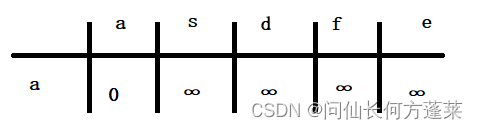
• 依次按 asdfe 的顺序遍历
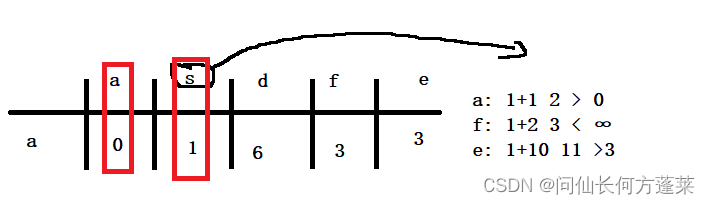
  • 取出顶点，
  • 获取当前顶点的所有边
  • 分别与当前顶点的值相加，若能使右边的数值变小，就更新右边的数值
  • 锁定当前顶点（如果只与右边比可忽略此步骤）
• 重复
  
  

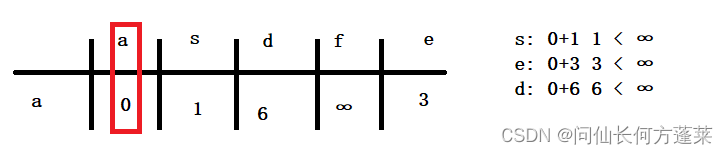
HashSet<Node> selecteds = new HashSet<>();
HashMap<Node,Integer> distances = new HashMap<>();
distances.put(node,0);
//selecteds.add(node);
min = node;
while(selecteds.size() < g.nodes.size()){
	int distance = distances.get(min);
	for(Edge e: min.edges){
		if(!distances.containsKey(e.to))
			distances.put(e.to,e.weight);
		
		if(distances.get(min)+e.weight < distances.get(e)){
			distances.put(e.to,distances.get(min)+e.weight);
		}
		selecteds.add(min);
		min = minOfDistancesAndUnselected(distances,selecteds);
	}
}
return distances;