数据压缩实验四 DPCM压缩系统的实现与分析

一、实验原理

1.DPCM编解码原理

     DPCM是差分预测编码调制的缩写，是比较典型的预测编码系统。预测编码是利用信源相邻符号间的相关性，根据某一模型利用以往的样本值对新样本进行预测，然后将样本的实际值与其预测值相减得到一个误差值，最后对其误差值进行编码。如果模型足够好，且样本序列在时间上相关性较强，则误差信号的幅度将远远小于原始信号，从而得到较大的数据压缩。

     DPCM编解码系统框图如下：

     

    其中Xk^是Xk的预测值，是前一个样本的解码值（重建值），所以编码器里实际内嵌了一个解码器，即图中红色框所示。

    将样本原始值Xk与预测值Xk^相减得到预测误差ek，对ek进行量化得到量化预测误差ek^。ek^除了送到编码器编码并输出外，还用于更新预测值。即将ek^和原预测值Xk^相加，构成预测值新的输入Xk'。

    DPCM系统的量化误差，即编码器输入原始值与量化后带有量化误差的重建值Xk'之差，    就是对预测误差ek量化引进的量化误差。

 

2.DPCM系统的设计

      在一个DPCM系统中需要设计两部分：预测器和量化器。理想情况下，预测器和量化器应进行联合优化。实际中，采用一种次优的设计方法：分别进行线性预测器和量化器的优化设计。

    在本次实验中，采用的是固定预测器和均匀量化器。预测器采用相邻左侧样本，量化器采用8bit均匀量化。

二、实验流程分析

   1、以实验二BMP2YUV为基础，读取一张BMP图像，转换提取其中的Y分量，存入yBuf缓冲区。

   2、循环遍历图像的每一个像素点，以相邻左侧样本的重建值作为预测值，原始值与预测值相减得到预测误差dev。

   3、对dev进行8bit量化，量化后的预测误差存入缓冲区Q_dev。

   4、将量化后的预测误差进行反量化，再与当前预测值（即前一样本的重建值）相加，得到当前样本的重建值，存入y_new缓冲区。

   5、输出量化预测误差图像和重建图像。将预测误差图像写入文件并送入Huffman编码器，与原始图像文件输入Huffman编码器进行比较。

三、关键代码及分析

创建三个缓冲区：

unsigned char* yBuf=(unsigned char*)malloc(width*height);///像素初始值缓冲区
unsigned char* y_new=(unsigned char*)malloc(width*height);///像素重建值缓冲区
unsigned char* Q_dev=(unsigned char*)malloc(width*height);///量化预测误差缓冲区

因为BMP图像提取Y分量后，得到的为灰度图，灰度值范围[0,255]。当前像素与前一像素重建值相减得到的预测误差范围[-255,255]，要进行8bit量化，可以直接对预测误差除以2，得到量化预测误差范围[-127,127]，再将量化预测误差做+128变换，将量化预测误差范围变换到[0,255]，可以输出相应图像文件。

再对量化预测误差进行反量化，即将量化预测误差做乘2运算。

for(i=0;i<width * height;i++)///遍历每一个像素
{
	float dev;///定义预测误差为浮点型
	if(i%width==0)///如果像素位于图像的第一列
	{
		dev=(float)(*(y+i)-128);///预测值选取128，原始值与预测值相减求出预测误差
		*(Q_dev+i)=(unsigned char)(dev/2+128);///对预测误差进行量化及灰度值变换
		*(y_new+i)=(*(Q_dev+i)-128)*2+128;///对量化预测误差进行反量化再与预测值相加得到重建值
	}
	else///如果像素不位于图像的第一列
	{
		dev=(float)(*(y+i)-*(y_new+i-1));///选取前一像素的重建值作为预测值
		*(Q_dev+i)=(unsigned char)(dev/2+128);
		*(y_new+i)=(*(Q_dev+i)-128)*2+*(y_new+i-1);

	}
}

 

最后将相应缓冲区写入文件：

fwrite(yBuf, 1, width * height, yuvFile);
fwrite(y_new,1,width*height,y_newFile);
fwrite(Q_dev,1,width*height,Q_devFile);

四、实验结果及分析

1、输入一张24位真彩图：

 

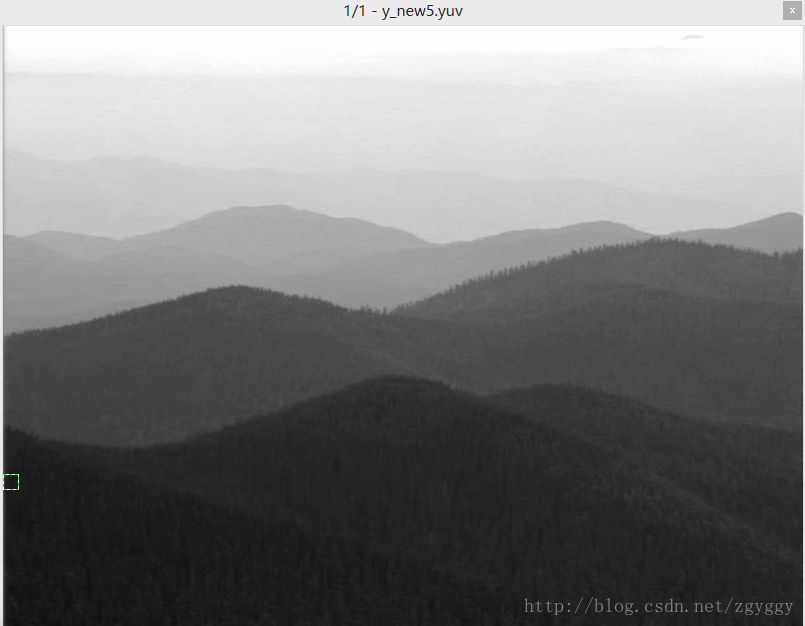
可以看到原图（左图）与重建图（右图）几乎无差别。

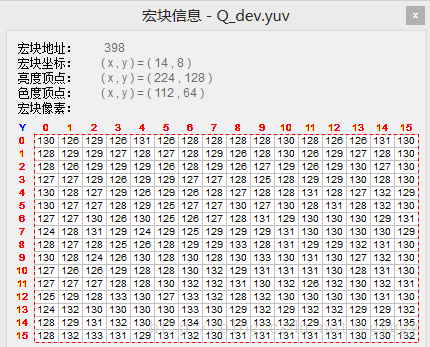
选取相同宏块的像素对比，可以发现有像素的灰度值不完全相同。例如原图坐标（0,7）像素值为119，其预测值为左侧像素（0,6）点的重建值112，预测误差为119-112=7，量化后预测误差7/2=3.5，由于输出到Q_dev缓冲区的数据为unsigned char型，浮点数3.5经过数据类型转换变为3，再反量化3*2=6，与预测值相加得到该点的重建值112+6=118，与原图对应像素值存在误差。

dev=(float)(*(y+i)-*(y_new+i-1));///选取前一像素的重建值作为预测值
*(Q_dev+i)=(unsigned char)(dev/2+128);
*(y_new+i)=(*(Q_dev+i)-128)*2+*(y_new+i-1);

 

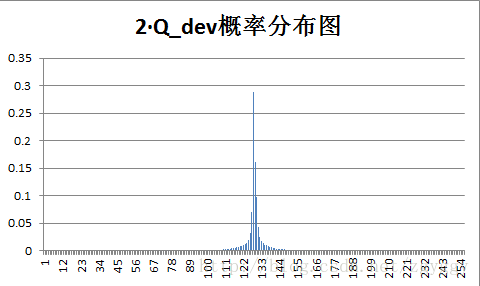
量化后的预测误差图像如下，其灰度值均集中在128附近。

2、再选用其他几组BMP图像进行测试：

 

 

 

 

其差值图像和量化预测误差图像如下：

 

 

将以上图像的原始图像文件和量化预测误差图像Q_dev文件分别送入Huffman编码器编码，得到输出码流。

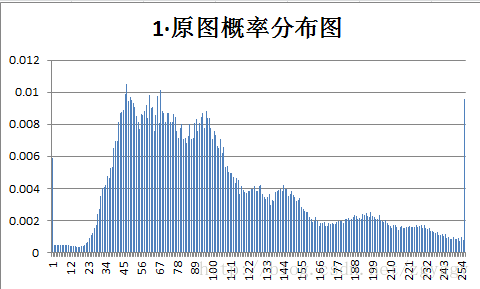
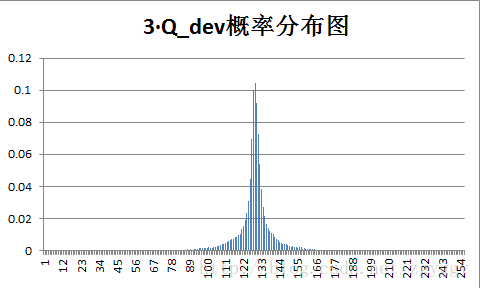
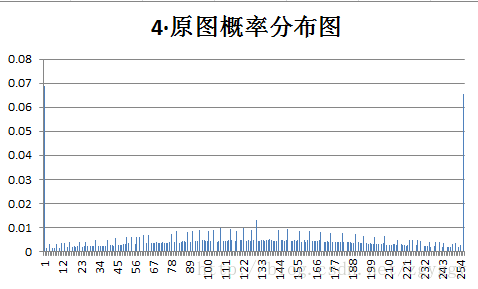
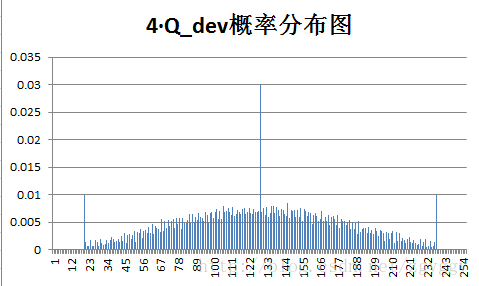
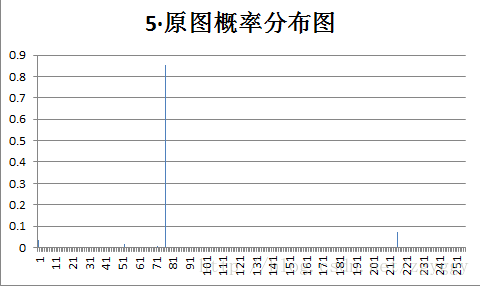
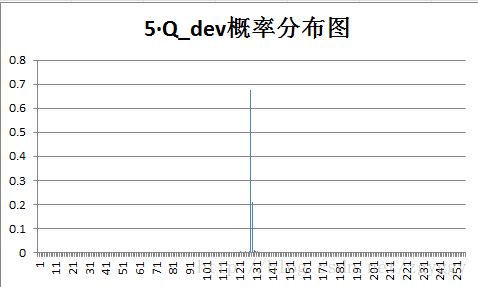
原始图像和量化预测误差图像概率分布如下：

 

 

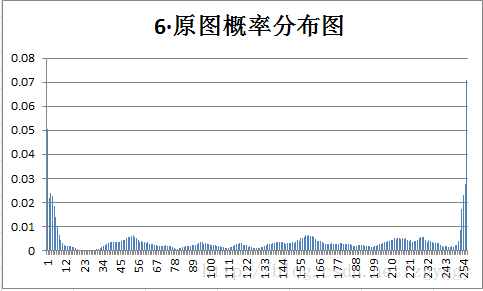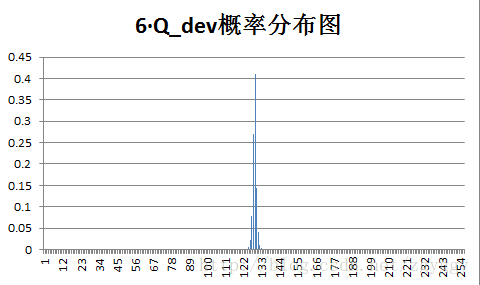不管原图的概率分布如何，量化后的预测误差值概率分布都变得集中，分布在0附近，经过+128转换后，预测误差值均集中在128附近。

 

原图文件压缩前大小（KB）	1153	66	193	66	66	1407
原图文件压缩后大小（KB）	1099	59	184	60	13	1283
原图文件压缩比	1.049	1.119	1.049	1.1	5.077	1.097
量化预测误差图像文件压缩前大小（KB）	384	64	64	64	64	469
量化预测误差图像文件压缩后大小（KB）	175	35	42	62	17	138
量化预测误差图像文件压缩比大小	2.194	1.828	1,524	1.032	3.765	3.398

可以看到，对于一般图像，对量化预测图像文件进行编码，比直接对原图进行编码，压缩比都有所提高。而对于第四幅图像（噪声图像），由于原图图像细节多，相邻像素间相关性较小，预测编码后的预测误差值分布也较为分散，压缩比得不到明显改善。

五、实验结论

 如果直接对原图编码，由于原始图像概率分布往往较为均匀分散，不能得到很好的压缩。而采用差分预测编码，即对量化后的预测误差值进行编码，由于预测误差值在整个取值范围[0,255]内分布极不均匀，通过Huffman编码后，压缩效率可以大大提高。这样在实际应用中运用差分预测编码可以节省许多的存储资源，减小传输带宽。