图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。

图的分类
无向图(Undirected Graph)
有向图(Directed Graph)



无权图(Unweighted Graph)
有权图(Weighted Graph)
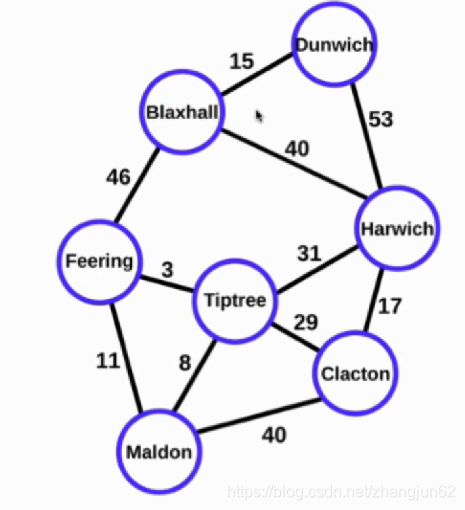
图的连通性
一张图中可以分为几个部分组成,不一定每部分相连通
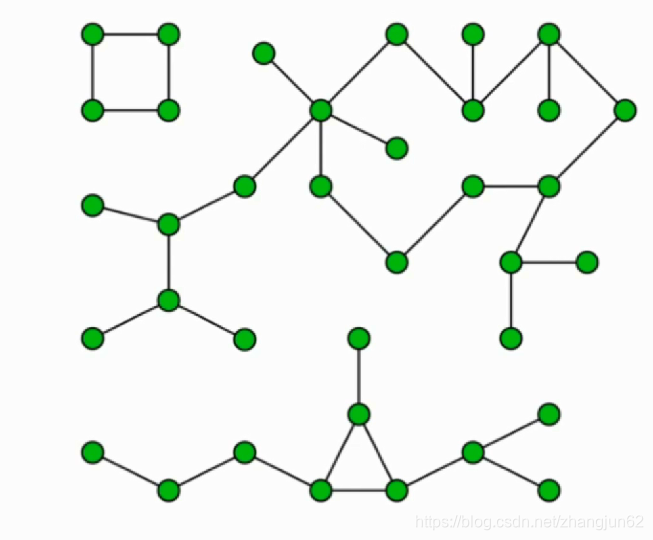
简单图(Simple Graph)

图的表示
邻接矩阵(Adjacency Matrix)


邻接表(Adjacency Lists)
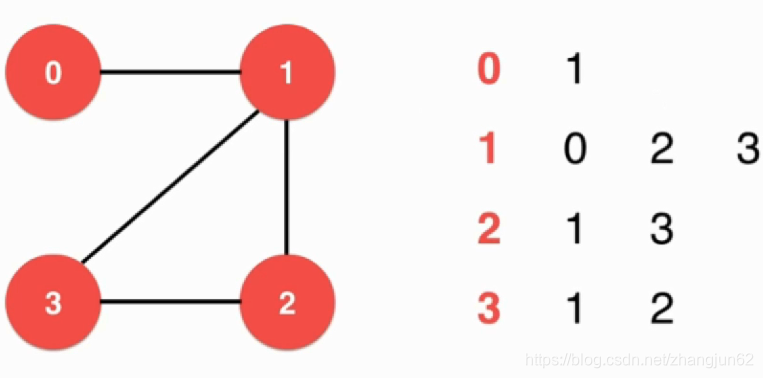

邻接矩阵和邻接表
邻接表适合表示稀疏图(Sparse Graph)
邻接矩阵适合表示稠密图(Dense Graph)
稀疏图
每个点边的的个数远小于图中点最大个数
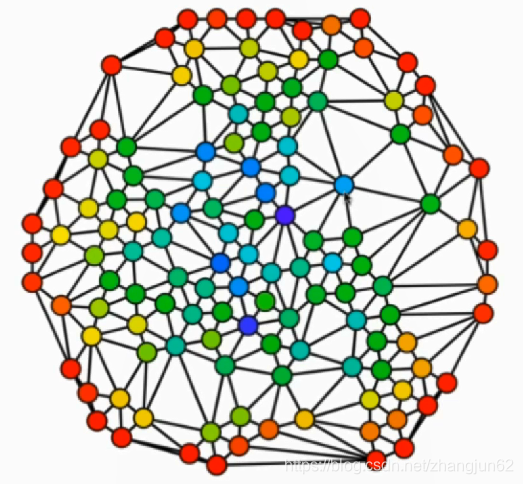
稠密图和完全图
使用Java来分别实现稀疏图和稠密图
import java.util.Vector;
//稀疏图 - 邻接表
public class SparseGraph {
private int n; // 节点数
private int m; // 边数
private boolean directed; // 是否为有向图
private Vector<Integer>[] g; // 图的具体数据
// 构造函数
public SparseGraph( int n , boolean directed ){
assert n >= 0;
this.n = n;
this.m = 0; // 初始化没有任何边
this.directed = directed;
// g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
g = (Vector<Integer>[])new Vector[n];
for(int i = 0 ; i < n ; i ++)
g[i] = new Vector<Integer>();
}
public int V(){ return n;} // 返回节点个数
public int E(){ return m;} // 返回边的个数
// 向图中添加一个边
public void addEdge( int v, int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
g[v].add(w);
if( v != w && !directed )
g[w].add(v);
m ++;
}
// 验证图中是否有从v到w的边
boolean hasEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
for( int i = 0 ; i < g[v].size() ; i ++ )
if( g[v].elementAt(i) == w )
return true;
return false;
}
//O(E)
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制,返回一个Vector不会带来额外开销
public Iterable<Integer> adj(int v) {
assert v >= 0 && v < n;
return g[v];
}
}
//稠密图 - 邻接矩阵
public class DenseGraph {
private int n; // 节点数
private int m; // 边数
private boolean directed; // 是否为有向图
private boolean[][] g; // 图的具体数据
// 构造函数
public DenseGraph( int n , boolean directed ){
assert n >= 0;
this.n = n;
this.m = 0; // 初始化没有任何边
this.directed = directed;
// g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
// false为boolean型变量的默认值
g = new boolean[n][n];
}
public int V(){ return n;} // 返回节点个数
public int E(){ return m;} // 返回边的个数
// 向图中添加一个边
public void addEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
if( hasEdge( v , w ) )
return;
g[v][w] = true;
if( !directed )
g[w][v] = true;
m ++;
}
// 验证图中是否有从v到w的边
boolean hasEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
return g[v][w];
}
//O(V^2)
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制,返回一个Vector不会带来额外开销,
public Iterable<Integer> adj(int v) {
assert v >= 0 && v < n;
Vector<Integer> adjV = new Vector<Integer>();
for(int i = 0 ; i < n ; i ++ )
if( g[v][i] )
adjV.add(i);
return adjV;
}
}编写测试程序
import cn.zjut.graph.DenseGraph;
import cn.zjut.graph.SparseGraph;
import java.util.Random;
public class Test {
public static void main(String[] args) {
int N = 20;
int M = 100;
Random random = new Random(0);
SparseGraph g1 = new SparseGraph(N, false);
for (int i = 0; i < M; i++) {
int a = random.nextInt(Integer.MAX_VALUE) % N;
int b = random.nextInt(Integer.MAX_VALUE) % N;
g1.addEdge(a, b);
}
for (int v = 0; v < N; v++){
System.out.print(v + " : ");
Iterable<Integer> adj = g1.adj(v);
adj.forEach(w-> System.out.print(w + " "));
System.out.println();
}
System.out.println();
DenseGraph g2 = new DenseGraph(N, false);
for (int i = 0; i < M; i++) {
int a = random.nextInt(Integer.MAX_VALUE) % N;
int b = random.nextInt(Integer.MAX_VALUE) % N;
g2.addEdge(a, b);
}
for (int v = 0; v < N; v++){
System.out.print(v + " : ");
Iterable<Integer> adj = g2.adj(v);
adj.forEach(w-> System.out.print(w + " "));
System.out.println();
}
}
}通过读取文件获取图信息构建图
testG1.txt
13 13
0 5
4 3
0 1
9 12
6 4
5 4
0 2
11 12
9 10
0 6
7 8
9 11
5 3其中第一行表示点数和边数
其余行表示一条边
testG2.txt
6 8
0 1
0 2
0 5
1 2
1 3
1 4
3 4
3 5创建一个图公共接口,稠密图和稀疏图都实现此接口
// 图的接口
public interface Graph {
public int V();
public int E();
public void addEdge( int v , int w );
boolean hasEdge( int v , int w );
void show();
public Iterable<Integer> adj(int v);
}稀疏图
// 稀疏图 - 邻接表
import java.util.Vector;
public class SparseGraph implements Graph {
private int n; // 节点数
private int m; // 边数
private boolean directed; // 是否为有向图
private Vector<Integer>[] g; // 图的具体数据
// 构造函数
public SparseGraph( int n , boolean directed ){
assert n >= 0;
this.n = n;
this.m = 0; // 初始化没有任何边
this.directed = directed;
// g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
g = (Vector<Integer>[])new Vector[n];
for(int i = 0 ; i < n ; i ++)
g[i] = new Vector<Integer>();
}
public int V(){ return n;} // 返回节点个数
public int E(){ return m;} // 返回边的个数
// 向图中添加一个边
public void addEdge( int v, int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
g[v].add(w);
if( v != w && !directed )
g[w].add(v);
m ++;
}
// 验证图中是否有从v到w的边
public boolean hasEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
for( int i = 0 ; i < g[v].size() ; i ++ )
if( g[v].elementAt(i) == w )
return true;
return false;
}
// 显示图的信息
public void show(){
for( int i = 0 ; i < n ; i ++ ){
System.out.print("vertex " + i + ":\t");
for( int j = 0 ; j < g[i].size() ; j ++ )
System.out.print(g[i].elementAt(j) + "\t");
System.out.println();
}
}
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制,返回一个Vector不会带来额外开销,
public Iterable<Integer> adj(int v) {
assert v >= 0 && v < n;
return g[v];
}
}稠密图
// 稠密图 - 邻接矩阵
import java.util.Vector;
public class DenseGraph implements Graph{
private int n; // 节点数
private int m; // 边数
private boolean directed; // 是否为有向图
private boolean[][] g; // 图的具体数据
// 构造函数
public DenseGraph( int n , boolean directed ){
assert n >= 0;
this.n = n;
this.m = 0; // 初始化没有任何边
this.directed = directed;
// g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
// false为boolean型变量的默认值
g = new boolean[n][n];
}
public int V(){ return n;} // 返回节点个数
public int E(){ return m;} // 返回边的个数
// 向图中添加一个边
public void addEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
if( hasEdge( v , w ) )
return;
g[v][w] = true;
if( !directed )
g[w][v] = true;
m ++;
}
// 验证图中是否有从v到w的边
public boolean hasEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
return g[v][w];
}
// 显示图的信息
public void show(){
for( int i = 0 ; i < n ; i ++ ){
for( int j = 0 ; j < n ; j ++ )
System.out.print(g[i][j]+"\t");
System.out.println();
}
}
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制,返回一个Vector不会带来额外开销,
public Iterable<Integer> adj(int v) {
assert v >= 0 && v < n;
Vector<Integer> adjV = new Vector<Integer>();
for(int i = 0 ; i < n ; i ++ )
if( g[v][i] )
adjV.add(i);
return adjV;
}
}读图文件工具类ReadGraph
import java.io.BufferedInputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.util.InputMismatchException;
import java.util.Locale;
import java.util.NoSuchElementException;
import java.util.Scanner;
public class ReadGraph {
private Scanner scanner;
public ReadGraph(Graph graph, String filename){
readFile(filename);
try {
int V = scanner.nextInt();
if (V < 0)
throw new IllegalArgumentException("number of vertices in a Graph must be nonnegative");
assert V == graph.V();
int E = scanner.nextInt();
if (E < 0)
throw new IllegalArgumentException("number of edges in a Graph must be nonnegative");
for (int i = 0; i < E; i++) {
int v = scanner.nextInt();
int w = scanner.nextInt();
assert v >= 0 && v < V;
assert w >= 0 && w < V;
graph.addEdge(v, w);
}
}
catch (InputMismatchException e) {
String token = scanner.next();
throw new InputMismatchException("attempts to read an 'int' value from input stream, but the next token is \"" + token + "\"");
}
catch (NoSuchElementException e) {
throw new NoSuchElementException("attemps to read an 'int' value from input stream, but there are no more tokens available");
}
}
private void readFile(String filename){
assert filename != null;
try {
File file = new File(filename);
if (file.exists()) {
FileInputStream fis = new FileInputStream(file);
scanner = new Scanner(new BufferedInputStream(fis), "UTF-8");
scanner.useLocale(Locale.ENGLISH);
}
else
throw new IllegalArgumentException(filename + "doesn't exist.");
}
catch (IOException ioe) {
throw new IllegalArgumentException("Could not open " + filename, ioe);
}
}
}编写测试程序
public class Main {
public static void main(String[] args) {
// 使用两种图的存储方式读取testG1.txt文件
String filename = "testG1.txt";
SparseGraph g1 = new SparseGraph(13, false);
ReadGraph readGraph1 = new ReadGraph(g1, filename);
System.out.println("test G1 in Sparse Graph:");
g1.show();
System.out.println();
DenseGraph g2 = new DenseGraph(13, false);
ReadGraph readGraph2 = new ReadGraph(g2 , filename );
System.out.println("test G1 in Dense Graph:");
g2.show();
System.out.println();
// 使用两种图的存储方式读取testG2.txt文件
filename = "testG2.txt";
SparseGraph g3 = new SparseGraph(6, false);
ReadGraph readGraph3 = new ReadGraph(g3, filename);
System.out.println("test G2 in Sparse Graph:");
g3.show();
System.out.println();
DenseGraph g4 = new DenseGraph(6, false);
ReadGraph readGraph4 = new ReadGraph(g4, filename);
System.out.println("test G2 in Dense Graph:");
g4.show();
}
}图的遍历
深度优先遍历
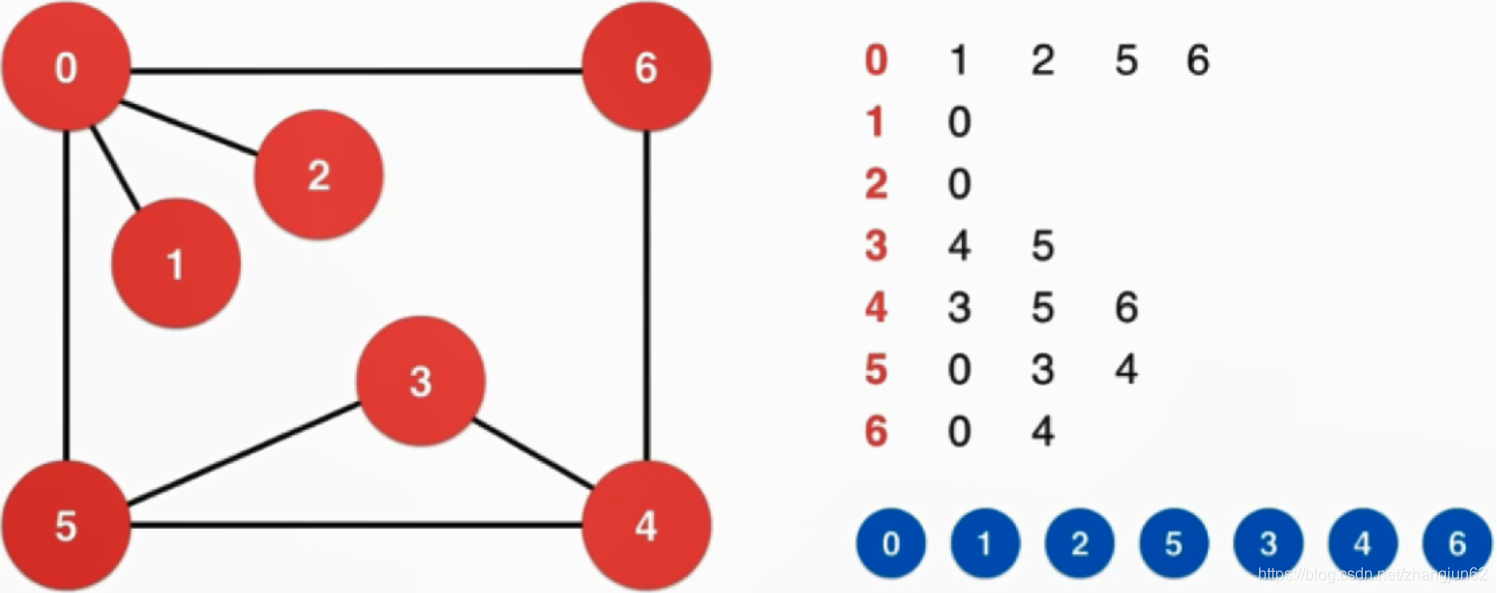
深度优先遍历可以求图中连通分量

将求图连通分量的算法封装在一个类中
// 求无权图的联通分量
public class Component {
private Graph G; // 图的引用
private boolean[] visited; // 记录dfs的过程中节点是否被访问
private int ccount; // 记录联通分量个数
private int[] id; // 每个节点所对应的联通分量标记
// 图的深度优先遍历
void dfs( int v ){
visited[v] = true;
id[v] = ccount;
for( int i: G.adj(v) ){
if( !visited[i] )
dfs(i);
}
}
// 构造函数, 求出无权图的联通分量
public Component(Graph graph){
// 算法初始化
G = graph;
visited = new boolean[G.V()];
id = new int[G.V()];
ccount = 0;
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
id[i] = -1;
}
// 求图的联通分量
for( int i = 0 ; i < G.V() ; i ++ )
if( !visited[i] ){
dfs(i);
ccount ++;
}
}
// 返回图的联通分量个数
int count(){
return ccount;
}
// 查询点v和点w是否联通
boolean isConnected( int v , int w ){
assert v >= 0 && v < G.V();
assert w >= 0 && w < G.V();
return id[v] == id[w];
}
}编写测试程序
public class Main {
public static void main(String[] args) {
// TestG1.txt
String filename1 = "testG1.txt";
SparseGraph g1 = new SparseGraph(13, false);
ReadGraph readGraph1 = new ReadGraph(g1, filename1);
Component component1 = new Component(g1);
System.out.println("TestG1.txt, Component Count: " + component1.count());
System.out.println();
// TestG2.txt
String filename2 = "testG2.txt";
SparseGraph g2 = new SparseGraph(6, false);
ReadGraph readGraph2 = new ReadGraph(g2, filename2);
Component component2 = new Component(g2);
System.out.println("TestG2.txt, Component Count: " + component2.count());
}
}使用深度优先遍历获取两点之间的一条路径
public class Path {
private Graph G; // 图的引用
private int s; // 起始点
private boolean[] visited; // 记录dfs的过程中节点是否被访问
private int[] from; // 记录路径, from[i]表示查找的路径上i的上一个节点
// 图的深度优先遍历
private void dfs( int v ){
visited[v] = true;
for( int i : G.adj(v) )
if( !visited[i] ){
from[i] = v;
dfs(i);
}
}
// 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
public Path(Graph graph, int s){
// 算法初始化
G = graph;
assert s >= 0 && s < G.V();
visited = new boolean[G.V()];
from = new int[G.V()];
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
from[i] = -1;
}
this.s = s;
// 寻路算法
dfs(s);
}
// 查询从s点到w点是否有路径
boolean hasPath(int w){
assert w >= 0 && w < G.V();
return visited[w];
}
// 查询从s点到w点的路径, 存放在vec中
Vector<Integer> path(int w){
assert hasPath(w) ;
Stack<Integer> s = new Stack<Integer>();
// 通过from数组逆向查找到从s到w的路径, 存放到栈中
int p = w;
while( p != -1 ){
s.push(p);
p = from[p];
}
// 从栈中依次取出元素, 获得顺序的从s到w的路径
Vector<Integer> res = new Vector<Integer>();
while( !s.empty() )
res.add( s.pop() );
return res;
}
// 打印出从s点到w点的路径
void showPath(int w){
assert hasPath(w) ;
Vector<Integer> vec = path(w);
for( int i = 0 ; i < vec.size() ; i ++ ){
System.out.print(vec.elementAt(i));
if( i == vec.size() - 1 )
System.out.println();
else
System.out.print(" -> ");
}
}
}编写测试程序
public class Main {
public static void main(String[] args) {
String filename = "testG.txt";
SparseGraph g = new SparseGraph(7, false);
ReadGraph readGraph = new ReadGraph(g, filename);
g.show();
System.out.println();
Path path = new Path(g,0);
System.out.println("Path from 0 to 6 : ");
path.showPath(6);
}
}图深度优先遍历复杂度
稀疏图(邻接表):O(V + E)
稠密图(邻接矩阵):O(V^2)
深度优先遍历算法对有向图依然有效
图广度优先遍历

广度优先遍历也叫程序遍历,后面遍历到的节点相对初始节点远一些
广度优先遍历求出无权图的最短路径
import java.util.Vector;
import java.util.Stack;
import java.util.LinkedList;
import java.util.Queue;
public class ShortestPath {
private Graph G; // 图的引用
private int s; // 起始点
private boolean[] visited; // 记录bfs的过程中节点是否被访问
private int[] from; // 记录路径, from[i]表示查找的路径上i的上一个节点
private int[] ord; // 记录路径中节点的次序。ord[i]表示i节点在路径中的次序。
// 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
public ShortestPath(Graph graph, int s){
// 算法初始化
G = graph;
assert s >= 0 && s < G.V();
visited = new boolean[G.V()];
from = new int[G.V()];
ord = new int[G.V()];
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
from[i] = -1;
ord[i] = -1;
}
this.s = s;
// 无向图最短路径算法, 从s开始广度优先遍历整张图
Queue<Integer> q = new LinkedList<Integer>();
q.add(s);
visited[s] = true;
ord[s] = 0;
while( !q.isEmpty() ){
int v = q.remove();
for( int i : G.adj(v) )
if( !visited[i] ){
q.add(i);
visited[i] = true;
from[i] = v;
ord[i] = ord[v] + 1;
}
}
}
// 查询从s点到w点是否有路径
public boolean hasPath(int w){
assert w >= 0 && w < G.V();
return visited[w];
}
// 查询从s点到w点的路径, 存放在vec中
public Vector<Integer> path(int w){
assert hasPath(w) ;
Stack<Integer> s = new Stack<Integer>();
// 通过from数组逆向查找到从s到w的路径, 存放到栈中
int p = w;
while( p != -1 ){
s.push(p);
p = from[p];
}
// 从栈中依次取出元素, 获得顺序的从s到w的路径
Vector<Integer> res = new Vector<Integer>();
while( !s.empty() )
res.add( s.pop() );
return res;
}
// 打印出从s点到w点的路径
public void showPath(int w){
assert hasPath(w) ;
Vector<Integer> vec = path(w);
for( int i = 0 ; i < vec.size() ; i ++ ){
System.out.print(vec.elementAt(i));
if( i == vec.size() - 1 )
System.out.println();
else
System.out.print(" -> ");
}
}
// 查看从s点到w点的最短路径长度
// 若从s到w不可达,返回-1
public int length(int w){
assert w >= 0 && w < G.V();
return ord[w];
}
}编写测试程序
public class Main {
public static void main(String[] args) {
String filename = "testG.txt";
SparseGraph g = new SparseGraph(7, false);
ReadGraph readGraph = new ReadGraph(g, filename);
g.show();
// 比较使用深度优先遍历和广度优先遍历获得路径的不同
// 广度优先遍历获得的是无权图的最短路径
Path dfs = new Path(g,0);
System.out.print("DFS : ");
dfs.showPath(6);
ShortestPath bfs = new ShortestPath(g,0);
System.out.print("BFS : ");
bfs.showPath(6);
System.out.println();
filename = "testG1.txt";
SparseGraph g2 = new SparseGraph(13, false);
ReadGraph readGraph2 = new ReadGraph(g2, filename);
g2.show();
// 比较使用深度优先遍历和广度优先遍历获得路径的不同
// 广度优先遍历获得的是无权图的最短路径
Path dfs2 = new Path(g2,0);
System.out.print("DFS : ");
dfs2.showPath(3);
ShortestPath bfs2 = new ShortestPath(g,0);
System.out.print("BFS : ");
bfs.showPath(3);
}
}图广度优先遍历复杂度
稀疏图(邻接表):O(V+E)
稠密图(邻接矩阵):O(V^2)
带权图Weighted Graph

实现有权图
对于有权图边的信息包含权值,直接将边封装为一个类,对于稀疏图就容易表示边的信息
// 边
public class Edge<Weight extends Number & Comparable> implements Comparable<Edge>{
private int a, b; // 边的两个端点
private Weight weight; // 边的权值
public Edge(int a, int b, Weight weight)
{
this.a = a;
this.b = b;
this.weight = weight;
}
public Edge(Edge<Weight> e)
{
this.a = e.a;
this.b = e.b;
this.weight = e.weight;
}
public int v(){ return a;} // 返回第一个顶点
public int w(){ return b;} // 返回第二个顶点
public Weight wt(){ return weight;} // 返回权值
// 给定一个顶点, 返回另一个顶点
public int other(int x){
assert x == a || x == b;
return x == a ? b : a;
}
// 输出边的信息
public String toString(){
return "" + a + "-" + b + ": " + weight;
}
// 边之间的比较
public int compareTo(Edge that)
{
if( weight.compareTo(that.wt()) < 0 )
return -1;
else if ( weight.compareTo(that.wt()) > 0 )
return +1;
else
return 0;
}
}实现有权图公共接口
interface WeightedGraph<Weight extends Number & Comparable> {
public int V();
public int E();
public void addEdge(Edge<Weight> e);
boolean hasEdge( int v , int w );
void show();
public Iterable<Edge<Weight>> adj(int v);
}
// 稠密图 - 邻接矩阵
public class DenseWeightedGraph<Weight extends Number & Comparable>
implements WeightedGraph{
private int n; // 节点数
private int m; // 边数
private boolean directed; // 是否为有向图
private Edge<Weight>[][] g; // 图的具体数据
// 构造函数
public DenseWeightedGraph( int n , boolean directed ){
assert n >= 0;
this.n = n;
this.m = 0; // 初始化没有任何边
this.directed = directed;
// g初始化为n*n的布尔矩阵, 每一个g[i][j]均为null, 表示没有任和边
// false为boolean型变量的默认值
g = new Edge[n][n];
for(int i = 0 ; i < n ; i ++)
for(int j = 0 ; j < n ; j ++)
g[i][j] = null;
}
public int V(){ return n;} // 返回节点个数
public int E(){ return m;} // 返回边的个数
// 向图中添加一个边
public void addEdge(Edge e){
assert e.v() >= 0 && e.v() < n ;
assert e.w() >= 0 && e.w() < n ;
if( hasEdge( e.v() , e.w() ) )
return;
g[e.v()][e.w()] = new Edge(e);
if( e.v() != e.w() && !directed )
g[e.w()][e.v()] = new Edge(e.w(), e.v(), e.wt());
m ++;
}
// 验证图中是否有从v到w的边
public boolean hasEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
return g[v][w] != null;
}
// 显示图的信息
public void show(){
for( int i = 0 ; i < n ; i ++ ){
for( int j = 0 ; j < n ; j ++ )
if( g[i][j] != null )
System.out.print(g[i][j].wt()+"\t");
else
System.out.print("NULL\t");
System.out.println();
}
}
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制,返回一个Vector不会带来额外开销,
public Iterable<Edge<Weight>> adj(int v) {
assert v >= 0 && v < n;
Vector<Edge<Weight>> adjV = new Vector<Edge<Weight>>();
for(int i = 0 ; i < n ; i ++ )
if( g[v][i] != null )
adjV.add( g[v][i] );
return adjV;
}
}
import java.util.Vector;
// 稀疏图 - 邻接表
public class SparseWeightedGraph<Weight extends Number & Comparable>
implements WeightedGraph {
private int n; // 节点数
private int m; // 边数
private boolean directed; // 是否为有向图
private Vector<Edge<Weight>>[] g; // 图的具体数据
// 构造函数
public SparseWeightedGraph( int n , boolean directed ){
assert n >= 0;
this.n = n;
this.m = 0; // 初始化没有任何边
this.directed = directed;
// g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
g = (Vector<Edge<Weight>>[])new Vector[n];
for(int i = 0 ; i < n ; i ++)
g[i] = new Vector<Edge<Weight>>();
}
public int V(){ return n;} // 返回节点个数
public int E(){ return m;} // 返回边的个数
// 向图中添加一个边, 权值为weight
public void addEdge(Edge e){
assert e.v() >= 0 && e.v() < n ;
assert e.w() >= 0 && e.w() < n ;
// 注意, 由于在邻接表的情况, 查找是否有重边需要遍历整个链表
// 我们的程序允许重边的出现
g[e.v()].add(new Edge(e));
if( e.v() != e.w() && !directed )
g[e.w()].add(new Edge(e.w(), e.v(), e.wt()));
m ++;
}
// 验证图中是否有从v到w的边
public boolean hasEdge( int v , int w ){
assert v >= 0 && v < n ;
assert w >= 0 && w < n ;
for( int i = 0 ; i < g[v].size() ; i ++ )
if( g[v].elementAt(i).other(v) == w )
return true;
return false;
}
// 显示图的信息
public void show(){
for( int i = 0 ; i < n ; i ++ ){
System.out.print("vertex " + i + ":\t");
for( int j = 0 ; j < g[i].size() ; j ++ ){
Edge e = g[i].elementAt(j);
System.out.print( "( to:" + e.other(i) + ",wt:" + e.wt() + ")\t");
}
System.out.println();
}
}
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制,返回一个Vector不会带来额外开销,
public Iterable<Edge<Weight>> adj(int v) {
assert v >= 0 && v < n;
return g[v];
}
}读取文件内容读取数据生成指定图
import java.io.BufferedInputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.util.Scanner;
import java.util.Locale;
import java.util.InputMismatchException;
import java.util.NoSuchElementException;
// 通过文件读取有全图的信息
public class ReadWeightedGraph{
private Scanner scanner;
// 由于文件格式的限制,我们的文件读取类只能读取权值为Double类型的图
public ReadWeightedGraph(WeightedGraph<Double> graph, String filename){
readFile(filename);
try {
int V = scanner.nextInt();
if (V < 0)
throw new IllegalArgumentException("number of vertices in a Graph must be nonnegative");
assert V == graph.V();
int E = scanner.nextInt();
if (E < 0)
throw new IllegalArgumentException("number of edges in a Graph must be nonnegative");
for (int i = 0; i < E; i++) {
int v = scanner.nextInt();
int w = scanner.nextInt();
Double weight = scanner.nextDouble();
assert v >= 0 && v < V;
assert w >= 0 && w < V;
graph.addEdge(new Edge<Double>(v, w, weight));
}
}
catch (InputMismatchException e) {
String token = scanner.next();
throw new InputMismatchException("attempts to read an 'int' value from input stream, but the next token is \"" + token + "\"");
}
catch (NoSuchElementException e) {
throw new NoSuchElementException("attemps to read an 'int' value from input stream, but there are no more tokens available");
}
}
private void readFile(String filename){
assert filename != null;
try {
File file = new File(filename);
if (file.exists()) {
FileInputStream fis = new FileInputStream(file);
scanner = new Scanner(new BufferedInputStream(fis), "UTF-8");
scanner.useLocale(Locale.ENGLISH);
}
else
throw new IllegalArgumentException(filename + " doesn't exist.");
}
catch (IOException ioe) {
throw new IllegalArgumentException("Could not open " + filename, ioe);
}
}
}最小生成树问题Minimum Span Tree
最小生成树保证各个结点之间均连通,连通路劲总权值最小,主要针对带权无向图和连通图。主要解决在一个图V条边中寻找V-1条边连接V个顶点,使得总权值最小

切分定理Cut Property
将图中结点分为两部分,成为一个切分(Cut)。如果一个边的两个端点,属于切分(Cut)不同两边,这个边称为横切边(Crossing Edge)。切分定理:给定任意切分,横切边中权值最小的边必然属于最小生成树。
Lazy Prim
一开始以0结点为起始点开始切分,通过将所有边加入到最小堆的方法获取一条最小权值横切边,再将这条边另一端结点合起来再一次切分,寻找最小权值横切边,如此循环下去,直到访问V个结点,获取V- 1条边,则算法停止,找到最小生成树。


实现Lazy Prim算法
由于每次需要获取横切边中最小权值的边,故采用最小堆作为辅助数据结构解决此问题。
// 在堆的有关操作中,需要比较堆中元素的大小,所以Item需要extends Comparable
public class MinHeap<Item extends Comparable> {
protected Item[] data;
protected int count;
protected int capacity;
// 构造函数, 构造一个空堆, 可容纳capacity个元素
public MinHeap(int capacity){
data = (Item[])new Comparable[capacity+1];
count = 0;
this.capacity = capacity;
}
// 构造函数, 通过一个给定数组创建一个最小堆
// 该构造堆的过程, 时间复杂度为O(n)
public MinHeap(Item arr[]){
int n = arr.length;
data = (Item[])new Comparable[n+1];
capacity = n;
for( int i = 0 ; i < n ; i ++ )
data[i+1] = arr[i];
count = n;
for( int i = count/2 ; i >= 1 ; i -- )
shiftDown(i);
}
// 返回堆中的元素个数
public int size(){
return count;
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty(){
return count == 0;
}
// 向最小堆中插入一个新的元素 item
public void insert(Item item){
assert count + 1 <= capacity;
data[count+1] = item;
count ++;
shiftUp(count);
}
// 从最小堆中取出堆顶元素, 即堆中所存储的最小数据
public Item extractMin(){
assert count > 0;
Item ret = data[1];
swap( 1 , count );
count --;
shiftDown(1);
return ret;
}
// 获取最小堆中的堆顶元素
public Item getMin(){
assert( count > 0 );
return data[1];
}
// 交换堆中索引为i和j的两个元素
private void swap(int i, int j){
Item t = data[i];
data[i] = data[j];
data[j] = t;
}
//********************
//* 最小堆核心辅助函数
//********************
private void shiftUp(int k){
while( k > 1 && data[k/2].compareTo(data[k]) > 0 ){
swap(k, k/2);
k /= 2;
}
}
private void shiftDown(int k){
while( 2*k <= count ){
int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
if( j+1 <= count && data[j+1].compareTo(data[j]) < 0 )
j ++;
// data[j] 是 data[2*k]和data[2*k+1]中的最小值
if( data[k].compareTo(data[j]) <= 0 ) break;
swap(k, j);
k = j;
}
}
}Lazy Prim实现类
import java.util.Vector;
// 使用Prim算法求图的最小生成树
public class LazyPrimMST<Weight extends Number & Comparable> {
private WeightedGraph<Weight> G; // 图的引用
private MinHeap<Edge<Weight>> pq; // 最小堆, 算法辅助数据结构
private boolean[] marked; // 标记数组, 在算法运行过程中标记节点i是否被访问
private Vector<Edge<Weight>> mst; // 最小生成树所包含的所有边
private Number mstWeight; // 最小生成树的权值
// 构造函数, 使用Prim算法求图的最小生成树
public LazyPrimMST(WeightedGraph<Weight> graph){
// 算法初始化
G = graph;
pq = new MinHeap<Edge<Weight>>(G.E());
marked = new boolean[G.V()];
mst = new Vector<Edge<Weight>>();
// Lazy Prim
visit(0);
while( !pq.isEmpty() ){
// 使用最小堆找出已经访问的边中权值最小的边
Edge<Weight> e = pq.extractMin();
// 如果这条边的两端都已经访问过了, 则扔掉这条边
if( marked[e.v()] == marked[e.w()] )
continue;
// 否则, 这条边则应该存在在最小生成树中
mst.add( e );
// 访问和这条边连接的还没有被访问过的节点
if( !marked[e.v()] )
visit( e.v() );
else
visit( e.w() );
}
// 计算最小生成树的权值
mstWeight = mst.elementAt(0).wt();
for( int i = 1 ; i < mst.size() ; i ++ )
mstWeight = mstWeight.doubleValue() + mst.elementAt(i).wt().doubleValue();
}
// 访问节点v
private void visit(int v){
assert !marked[v];
marked[v] = true;
// 将和节点v相连接的所有未访问的边放入最小堆中
for( Edge<Weight> e : G.adj(v) )
if( !marked[e.other(v)] )
pq.insert(e);
}
// 返回最小生成树的所有边
Vector<Edge<Weight>> mstEdges(){
return mst;
}
// 返回最小生成树的权值
Number result(){
return mstWeight;
}
}测试类
import java.util.Vector;
public class Main {
public static void main(String[] args) {
String filename = "testG3.txt";
int V = 8;
SparseWeightedGraph<Double> g = new SparseWeightedGraph<Double>(V, false);
ReadWeightedGraph readGraph = new ReadWeightedGraph(g, filename);
// Test Lazy Prim MST
System.out.println("Test Lazy Prim MST:");
LazyPrimMST<Double> lazyPrimMST = new LazyPrimMST<Double>(g);
Vector<Edge<Double>> mst = lazyPrimMST.mstEdges();
for( int i = 0 ; i < mst.size() ; i ++ )
System.out.println(mst.elementAt(i));
System.out.println("The MST weight is: " + lazyPrimMST.result());
System.out.println();
}
}Prim算法优化
Lazy Prim算法时间复杂度为O(E log E),需要将其优化到O(E log V)。Lazy Prim主要问题是所有边都要进入到最小堆,随着切分的继续,切分结点增多,很多边已经不可能是横切边,虽然很多横切边,通常只会关注权值最小的横切边,尤其是和一个结点相连的最短横切边。因此需要最小索引堆这个数据结构保存并更新每个结点最短横切边权值,只需生成结点个数大小的最小索引堆,每次切分后只需将一个结点相连横切边加入堆,找到当前切分下最下横切边,同时这条横切边不参与下面计算当中。堆结构变小,同时访问边次数也少,优化时间消耗。

最小索引堆实现类
// 最小索引堆
public class IndexMinHeap<Item extends Comparable> {
protected Item[] data; // 最小索引堆中的数据
protected int[] indexes; // 最小索引堆中的索引, indexes[x] = i 表示索引i在x的位置
protected int[] reverse; // 最小索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置
protected int count;
protected int capacity;
// 构造函数, 构造一个空堆, 可容纳capacity个元素
public IndexMinHeap(int capacity){
data = (Item[])new Comparable[capacity+1];
indexes = new int[capacity+1];
reverse = new int[capacity+1];
for( int i = 0 ; i <= capacity ; i ++ )
reverse[i] = 0;
count = 0;
this.capacity = capacity;
}
// 返回索引堆中的元素个数
public int size(){
return count;
}
// 返回一个布尔值, 表示索引堆中是否为空
public boolean isEmpty(){
return count == 0;
}
// 向最小索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
public void insert(int i, Item item){
assert count + 1 <= capacity;
assert i + 1 >= 1 && i + 1 <= capacity;
// 再插入一个新元素前,还需要保证索引i所在的位置是没有元素的。
assert !contain(i);
i += 1;
data[i] = item;
indexes[count+1] = i;
reverse[i] = count + 1;
count ++;
shiftUp(count);
}
// 从最小索引堆中取出堆顶元素, 即索引堆中所存储的最小数据
public Item extractMin(){
assert count > 0;
Item ret = data[indexes[1]];
swapIndexes( 1 , count );
reverse[indexes[count]] = 0;
count --;
shiftDown(1);
return ret;
}
// 从最小索引堆中取出堆顶元素的索引
public int extractMinIndex(){
assert count > 0;
int ret = indexes[1] - 1;
swapIndexes( 1 , count );
reverse[indexes[count]] = 0;
count --;
shiftDown(1);
return ret;
}
// 获取最小索引堆中的堆顶元素
public Item getMin(){
assert count > 0;
return data[indexes[1]];
}
// 获取最小索引堆中的堆顶元素的索引
public int getMinIndex(){
assert count > 0;
return indexes[1]-1;
}
// 看索引i所在的位置是否存在元素
boolean contain( int i ){
assert i + 1 >= 1 && i + 1 <= capacity;
return reverse[i+1] != 0;
}
// 获取最小索引堆中索引为i的元素
public Item getItem( int i ){
assert contain(i);
return data[i+1];
}
// 将最小索引堆中索引为i的元素修改为newItem
public void change( int i , Item newItem ){
assert contain(i);
i += 1;
data[i] = newItem;
// 有了 reverse 之后,
// 我们可以非常简单的通过reverse直接定位索引i在indexes中的位置
shiftUp( reverse[i] );
shiftDown( reverse[i] );
}
// 交换索引堆中的索引i和j
// 由于有了反向索引reverse数组,
// indexes数组发生改变以后, 相应的就需要维护reverse数组
private void swapIndexes(int i, int j){
int t = indexes[i];
indexes[i] = indexes[j];
indexes[j] = t;
reverse[indexes[i]] = i;
reverse[indexes[j]] = j;
}
//********************
//* 最小索引堆核心辅助函数
//********************
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftUp(int k){
while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) > 0 ){
swapIndexes(k, k/2);
k /= 2;
}
}
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftDown(int k){
while( 2*k <= count ){
int j = 2*k;
if( j+1 <= count && data[indexes[j+1]].compareTo(data[indexes[j]]) < 0 )
j ++;
if( data[indexes[k]].compareTo(data[indexes[j]]) <= 0 )
break;
swapIndexes(k, j);
k = j;
}
}
// 测试 IndexMinHeap
public static void main(String[] args) {
int N = 1000000;
IndexMinHeap<Integer> indexMinHeap = new IndexMinHeap<Integer>(N);
for( int i = 0 ; i < N ; i ++ )
indexMinHeap.insert( i , (int)(Math.random()*N) );
}
}Prim MST实现
import java.util.Vector;
// 使用优化的Prim算法求图的最小生成树
public class PrimMST<Weight extends Number & Comparable> {
private WeightedGraph G; // 图的引用
private IndexMinHeap<Weight> ipq; // 最小索引堆, 算法辅助数据结构
private Edge<Weight>[] edgeTo; // 访问的点所对应的边, 算法辅助数据结构
private boolean[] marked; // 标记数组, 在算法运行过程中标记节点i是否被访问
private Vector<Edge<Weight>> mst; // 最小生成树所包含的所有边
private Number mstWeight; // 最小生成树的权值
// 构造函数, 使用Prim算法求图的最小生成树
public PrimMST(WeightedGraph graph){
G = graph;
assert( graph.E() >= 1 );
ipq = new IndexMinHeap<Weight>(graph.V());
// 算法初始化
marked = new boolean[G.V()];
edgeTo = new Edge[G.V()];
for( int i = 0 ; i < G.V() ; i ++ ){
marked[i] = false;
edgeTo[i] = null;
}
mst = new Vector<Edge<Weight>>();
// Prim
visit(0);
while( !ipq.isEmpty() ){
// 使用最小索引堆找出已经访问的边中权值最小的边
// 最小索引堆中存储的是点的索引, 通过点的索引找到相对应的边
int v = ipq.extractMinIndex();
assert( edgeTo[v] != null );
mst.add( edgeTo[v] );
visit( v );
}
// 计算最小生成树的权值
mstWeight = mst.elementAt(0).wt();
for( int i = 1 ; i < mst.size() ; i ++ )
mstWeight = mstWeight.doubleValue() + mst.elementAt(i).wt().doubleValue();
}
// 访问节点v
void visit(int v){
assert !marked[v];
marked[v] = true;
// 将和节点v相连接的未访问的另一端点, 和与之相连接的边, 放入最小堆中
for( Object item : G.adj(v) ){
Edge<Weight> e = (Edge<Weight>)item;
int w = e.other(v);
// 如果边的另一端点未被访问
if( !marked[w] ){
// 如果从没有考虑过这个端点, 直接将这个端点和与之相连接的边加入索引堆
if( edgeTo[w] == null ){
edgeTo[w] = e;
ipq.insert(w, e.wt());
}
// 如果曾经考虑这个端点, 但现在的边比之前考虑的边更短, 则进行替换
else if( e.wt().compareTo(edgeTo[w].wt()) < 0 ){
edgeTo[w] = e;
ipq.change(w, e.wt());
}
}
}
}
// 返回最小生成树的所有边
Vector<Edge<Weight>> mstEdges(){
return mst;
}
// 返回最小生成树的权值
Number result(){
return mstWeight;
}
// 测试 Prim
public static void main(String[] args) {
String filename = "testG1.txt";
int V = 8;
SparseWeightedGraph<Double> g = new SparseWeightedGraph<Double>(V, false);
ReadWeightedGraph readGraph = new ReadWeightedGraph(g, filename);
// Test Prim MST
System.out.println("Test Prim MST:");
PrimMST<Double> primMST = new PrimMST<Double>(g);
Vector<Edge<Double>> mst = primMST.mstEdges();
for( int i = 0 ; i < mst.size() ; i ++ )
System.out.println(mst.elementAt(i));
System.out.println("The MST weight is: " + primMST.result());
System.out.println();
}
}Kruskal算法
首先在所有边中找到一个权值最小的边,成为最小生成树一条边,因为总有一种切分可以满足这条边是最小权值横切边。按照这种方式,不断寻找最短边来生成最小生成树,只要新的边加入不构成环则是一条正确的横切边,如果构成环则放弃这条最小权值边,继续搜索剩余最小权值边,直到生成整个最下生成树。每次都要对边进行排序,时间复杂度是E log E,但是判断是否有环需要消耗时间,对于比较小的图可以使用此种算法。对于是否形成环,可以采用并查集这个数据结构来实现。


并查集实现
// Union-Find
public class UnionFind {
// rank[i]表示以i为根的集合所表示的树的层数
// 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不在是树的层数值
// 这也是我们的rank不叫height或者depth的原因, 他只是作为比较的一个标准
private int[] rank;
private int[] parent; // parent[i]表示第i个元素所指向的父节点
private int count; // 数据个数
// 构造函数
public UnionFind(int count){
rank = new int[count];
parent = new int[count];
this.count = count;
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for( int i = 0 ; i < count ; i ++ ){
parent[i] = i;
rank[i] = 1;
}
}
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
int find(int p){
assert( p >= 0 && p < count );
// path compression 1
while( p != parent[p] ){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
// 查看元素p和元素q是否所属一个集合
// O(h)复杂度, h为树的高度
boolean isConnected( int p , int q ){
return find(p) == find(q);
}
// 合并元素p和元素q所属的集合
// O(h)复杂度, h为树的高度
void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
// 根据两个元素所在树的元素个数不同判断合并方向
// 将元素个数少的集合合并到元素个数多的集合上
if( rank[pRoot] < rank[qRoot] ){
parent[pRoot] = qRoot;
}
else if( rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
else{ // rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot] += 1; // 此时, 我维护rank的值
}
}
}Kruskal实现类
import java.util.Vector;
// Kruskal算法求最小生成树
public class KruskalMST<Weight extends Number & Comparable> {
private Vector<Edge<Weight>> mst; // 最小生成树所包含的所有边
private Number mstWeight; // 最小生成树的权值
// 构造函数, 使用Kruskal算法计算graph的最小生成树
public KruskalMST(WeightedGraph graph){
mst = new Vector<Edge<Weight>>();
// 将图中的所有边存放到一个最小堆中
MinHeap<Edge<Weight>> pq = new MinHeap<Edge<Weight>>( graph.E() );
for( int i = 0 ; i < graph.V() ; i ++ )
for( Object item : graph.adj(i) ){
Edge<Weight> e = (Edge<Weight>)item;
if( e.v() <= e.w() )
pq.insert(e);
}
// 创建一个并查集, 来查看已经访问的节点的联通情况
UnionFind uf = new UnionFind(graph.V());
while( !pq.isEmpty() && mst.size() < graph.V() - 1 ){
// 从最小堆中依次从小到大取出所有的边
Edge<Weight> e = pq.extractMin();
// 如果该边的两个端点是联通的, 说明加入这条边将产生环, 扔掉这条边
if( uf.isConnected( e.v() , e.w() ) )
continue;
// 否则, 将这条边添加进最小生成树, 同时标记边的两个端点联通
mst.add( e );
uf.unionElements( e.v() , e.w() );
}
// 计算最小生成树的权值
mstWeight = mst.elementAt(0).wt();
for( int i = 1 ; i < mst.size() ; i ++ )
mstWeight = mstWeight.doubleValue() + mst.elementAt(i).wt().doubleValue();
}
// 返回最小生成树的所有边
Vector<Edge<Weight>> mstEdges(){
return mst;
}
// 返回最小生成树的权值
Number result(){
return mstWeight;
}
// 测试 Kruskal
public static void main(String[] args) {
String filename = "testG1.txt";
int V = 8;
SparseWeightedGraph<Double> g = new SparseWeightedGraph<Double>(V, false);
ReadWeightedGraph readGraph = new ReadWeightedGraph(g, filename);
// Test Kruskal
System.out.println("Test Kruskal:");
KruskalMST<Double> kruskalMST = new KruskalMST<Double>(g);
Vector<Edge<Double>> mst = kruskalMST.mstEdges();
for( int i = 0 ; i < mst.size() ; i ++ )
System.out.println(mst.elementAt(i));
System.out.println("The MST weight is: " + kruskalMST.result());
System.out.println();
}
}如果存在权值相等的横切边,根据算法的具体实现,每次选择一个边,此时图中存在多个最小生成树,这些生成树最后最小权值和是一样的,对于前面算法只能找到一种最小生成树,如果权值各不相同,就只存在一种最小生成树。
Vyssotsky's Algorithm
该算法是将边逐渐地添加到生成树中,一旦形成环,删除环中权值最大边。
时间复杂度
Lazy Prim O( E log E)
Prim O( E log V)
Kruskal O( E log E)
最短路径问题Shortest Path
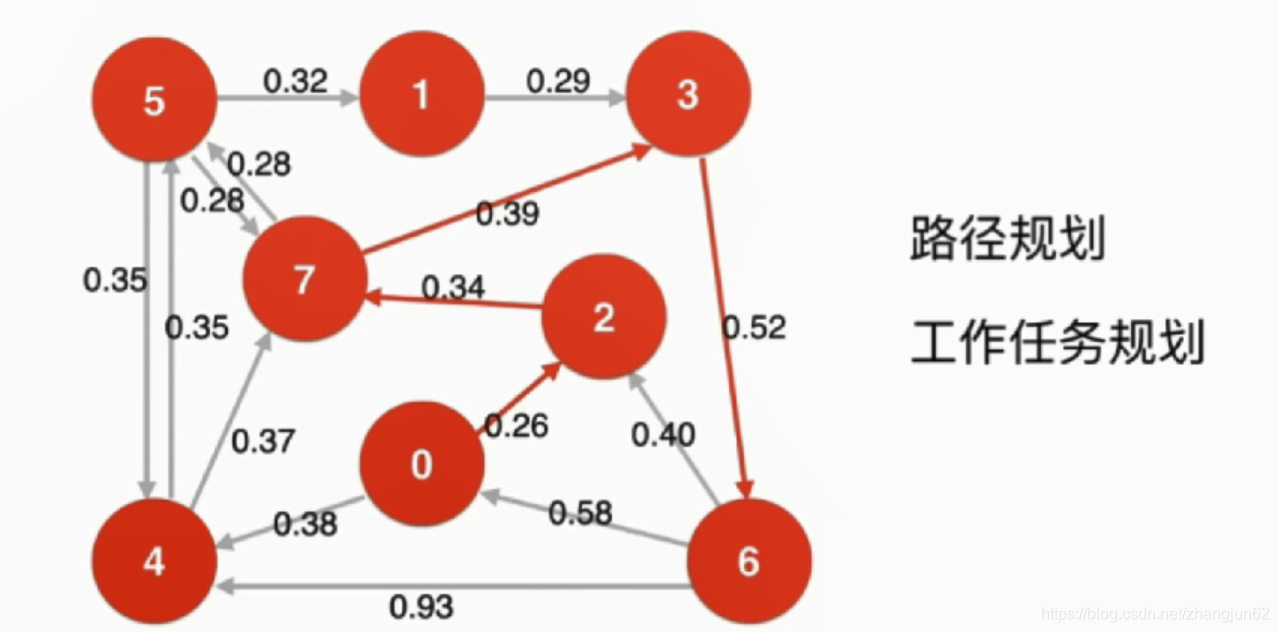
对于无权图,从起始点出发进行广度优先遍历,可以求出一个最短路径,其实求出的是从一个结点开始到其它所有结点的最短路径,形成以起始节点开始的最短路径树,解决的是单源最短路径问题。
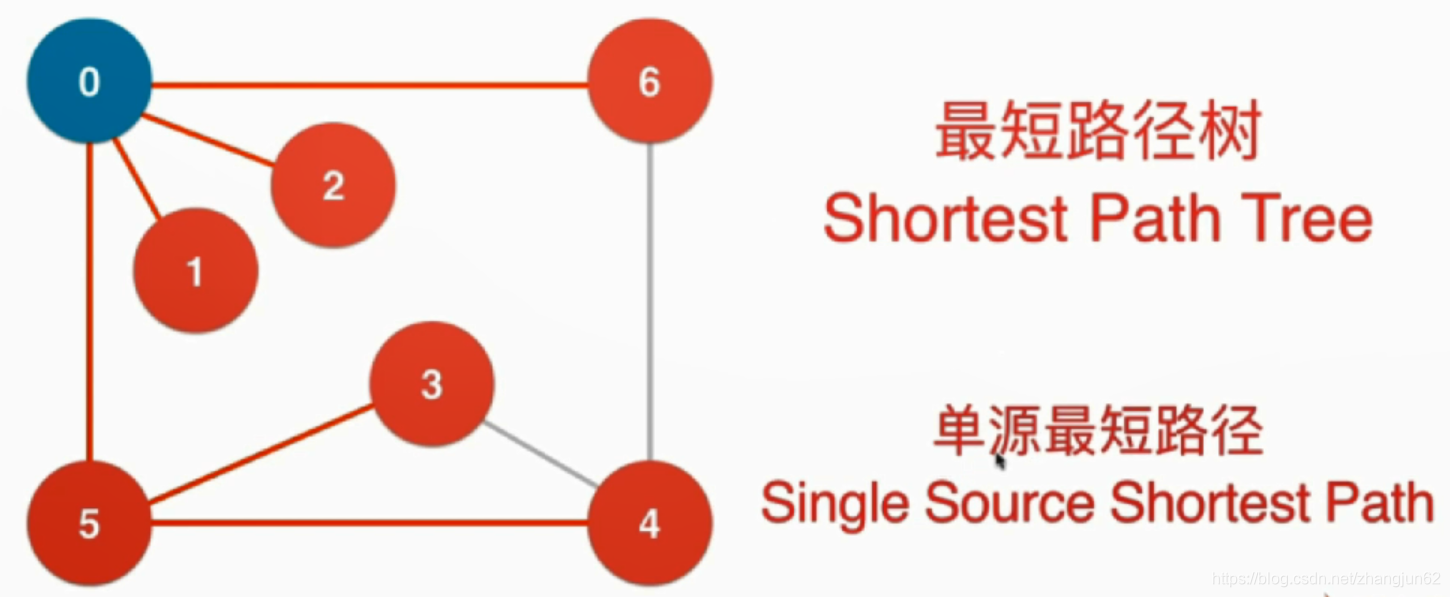
无权图最短路径

有权图的最短路径

松弛操作是求一个点到另一个点最短路径时考虑源点经过其它点再到目标点的路径是否还要小,不是以经过结点个数多少而是根据权值来判断最短路径,松弛操作是最短路径求解的核心。
Dijkstra单源最短路径算法
算法前提:图中不能有负权边。时间复杂度是O(E log (V))



实现此算法采用最小索引堆保存源点到每个点的最短路径,根据不断的遍历更新修改最短路径。
Dijkstra算法实现类
import java.util.Stack;
import java.util.Vector;
// Dijkstra算法求最短路径
public class Dijkstra<Weight extends Number & Comparable> {
private WeightedGraph G; // 图的引用
private int s; // 起始点
private Number[] distTo; // distTo[i]存储从起始点s到i的最短路径长度
private boolean[] marked; // 标记数组, 在算法运行过程中标记节点i是否被访问
private Edge<Weight>[] from; // from[i]记录最短路径中, 到达i点的边是哪一条
// 可以用来恢复整个最短路径
// 构造函数, 使用Dijkstra算法求最短路径
public Dijkstra(WeightedGraph graph, int s){
// 算法初始化
G = graph;
assert s >= 0 && s < G.V();
this.s = s;
distTo = new Number[G.V()];
marked = new boolean[G.V()];
from = new Edge[G.V()];
for( int i = 0 ; i < G.V() ; i ++ ){
distTo[i] = 0.0;
marked[i] = false;
from[i] = null;
}
// 使用索引堆记录当前找到的到达每个顶点的最短距离
IndexMinHeap<Weight> ipq = new IndexMinHeap<Weight>(G.V());
// 对于其实点s进行初始化
distTo[s] = 0.0;
from[s] = new Edge<Weight>(s, s, (Weight)(Number)(0.0));
ipq.insert(s, (Weight)distTo[s] );
marked[s] = true;
while( !ipq.isEmpty() ){
int v = ipq.extractMinIndex();
// distTo[v]就是s到v的最短距离
marked[v] = true;
// 对v的所有相邻节点进行更新
for( Object item : G.adj(v) ){
Edge<Weight> e = (Edge<Weight>)item;
int w = e.other(v);
// 如果从s点到w点的最短路径还没有找到
if( !marked[w] ){
// 如果w点以前没有访问过,
// 或者访问过, 但是通过当前的v点到w点距离更短, 则进行更新
if( from[w] == null || distTo[v].doubleValue() + e.wt().doubleValue() < distTo[w].doubleValue() ){
distTo[w] = distTo[v].doubleValue() + e.wt().doubleValue();
from[w] = e;
if( ipq.contain(w) )
ipq.change(w, (Weight)distTo[w] );
else
ipq.insert(w, (Weight)distTo[w] );
}
}
}
}
}
// 返回从s点到w点的最短路径长度
Number shortestPathTo( int w ){
assert w >= 0 && w < G.V();
assert hasPathTo(w);
return distTo[w];
}
// 判断从s点到w点是否联通
boolean hasPathTo( int w ){
assert w >= 0 && w < G.V() ;
return marked[w];
}
// 寻找从s到w的最短路径, 将整个路径经过的边存放在vec中
Vector<Edge<Weight>> shortestPath( int w){
assert w >= 0 && w < G.V();
assert hasPathTo(w);
// 通过from数组逆向查找到从s到w的路径, 存放到栈中
Stack<Edge<Weight>> s = new Stack<Edge<Weight>>();
Edge<Weight> e = from[w];
while( e.v() != this.s ){
s.push(e);
e = from[e.v()];
}
s.push(e);
// 从栈中依次取出元素, 获得顺序的从s到w的路径
Vector<Edge<Weight>> res = new Vector<Edge<Weight>>();
while( !s.empty() ){
e = s.pop();
res.add( e );
}
return res;
}
// 打印出从s点到w点的路径
void showPath(int w){
assert w >= 0 && w < G.V();
assert hasPathTo(w);
Vector<Edge<Weight>> path = shortestPath(w);
for( int i = 0 ; i < path.size() ; i ++ ){
System.out.print( path.elementAt(i).v() + " -> ");
if( i == path.size()-1 )
System.out.println(path.elementAt(i).w());
}
}
}处理负权边
对于负权边,Dijstra算法失效,但是仍然需要松弛操作。负权边的存在,可以产生负权环,对于拥有负权环的图,没有最短路径,因为绕着负权环一直转下去会使得权值趋于负无穷,无法收敛。

Bellman-Ford单源最短路径算法
算法前提:图中不能拥有负权环。对于这个前提条件,对于此算法不是算法开始就必须的,Bellman-Ford可以判断图中是否有负权环。时间复杂度是O(EV)。如果一个图中没有负权环,从一点到另外一点的最短路径,最多经过所有的V个顶点,有V-1条边,否则,存在顶点经过了两次,即存在负权环。
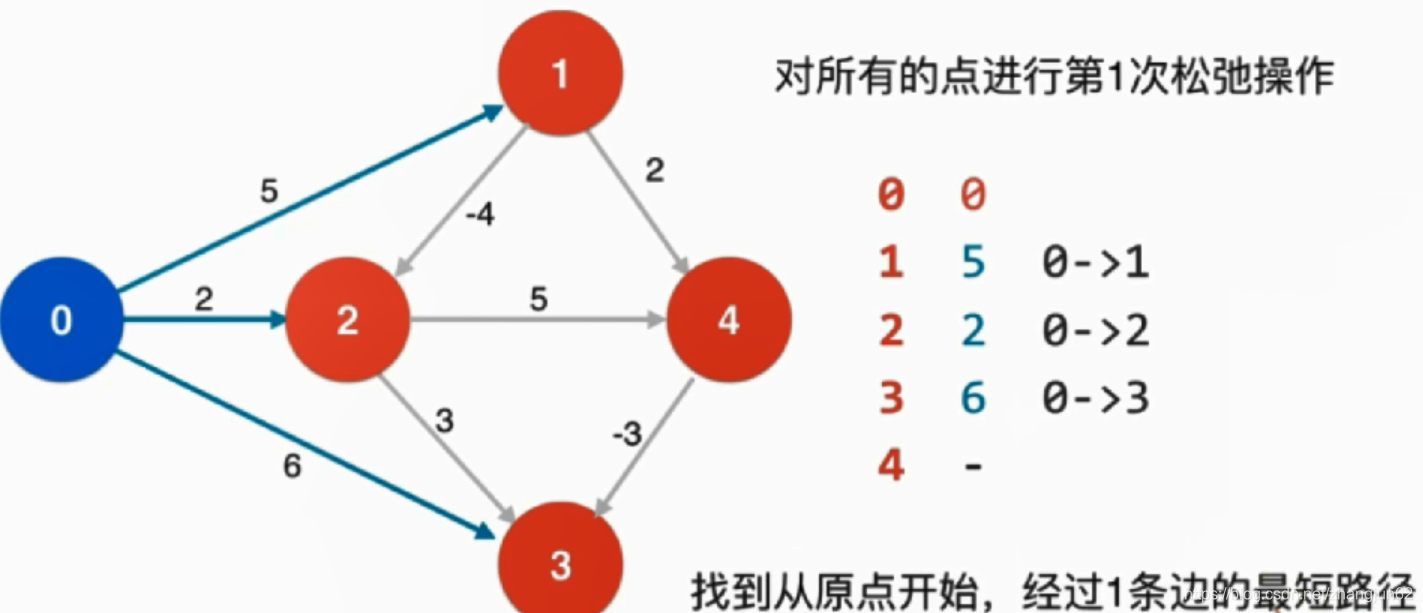

对一个点的一次松弛操作,就是找到经过这个点的另外一点路径,多一条边,权值更小。如果一个图中没有负权环,从一点到另外一点的最短路径,最多经过所有的V个顶点,有V-1条边。对所有点进行V-1次松弛操作,理论上就找到从源点到其他所有点的最短路径。如果还可以继续松弛,说明图中有负权环。
算法实现类
import java.util.Vector;
import java.util.Stack;
// 使用BellmanFord算法求最短路径
public class BellmanFord<Weight extends Number & Comparable> {
private WeightedGraph G; // 图的引用
private int s; // 起始点
private Number[] distTo; // distTo[i]存储从起始点s到i的最短路径长度
Edge<Weight>[] from; // from[i]记录最短路径中, 到达i点的边是哪一条
// 可以用来恢复整个最短路径
boolean hasNegativeCycle; // 标记图中是否有负权环
// 构造函数, 使用BellmanFord算法求最短路径
public BellmanFord(WeightedGraph graph, int s){
G = graph;
this.s = s;
distTo = new Number[G.V()];
from = new Edge[G.V()];
// 初始化所有的节点s都不可达, 由from数组来表示
for( int i = 0 ; i < G.V() ; i ++ )
from[i] = null;
// 设置distTo[s] = 0, 并且让from[s]不为NULL, 表示初始s节点可达且距离为0
distTo[s] = 0.0;
from[s] = new Edge<Weight>(s, s, (Weight)(Number)(0.0)); // 这里我们from[s]的内容是new出来的, 注意要在析构函数里delete掉
// Bellman-Ford的过程
// 进行V-1次循环, 每一次循环求出从起点到其余所有点, 最多使用pass步可到达的最短距离
for( int pass = 1 ; pass < G.V() ; pass ++ ){
// 每次循环中对所有的边进行一遍松弛操作
// 遍历所有边的方式是先遍历所有的顶点, 然后遍历和所有顶点相邻的所有边
for( int i = 0 ; i < G.V() ; i ++ ){
// 使用我们实现的邻边迭代器遍历和所有顶点相邻的所有边
for( Object item : G.adj(i) ){
Edge<Weight> e = (Edge<Weight>)item;
// 对于每一个边首先判断e->v()可达
// 之后看如果e->w()以前没有到达过, 显然我们可以更新distTo[e->w()]
// 或者e->w()以前虽然到达过, 但是通过这个e我们可以获得一个更短的距离, 即可以进行一次松弛操作, 我们也可以更新distTo[e->w()]
if( from[e.v()] != null && (from[e.w()] == null || distTo[e.v()].doubleValue() + e.wt().doubleValue() < distTo[e.w()].doubleValue()) ){
distTo[e.w()] = distTo[e.v()].doubleValue() + e.wt().doubleValue();
from[e.w()] = e;
}
}
}
}
hasNegativeCycle = detectNegativeCycle();
}
// 判断图中是否有负权环
boolean detectNegativeCycle(){
for( int i = 0 ; i < G.V() ; i ++ ){
for( Object item : G.adj(i) ){
Edge<Weight> e = (Edge<Weight>)item;
if( from[e.v()] != null && distTo[e.v()].doubleValue() + e.wt().doubleValue() < distTo[e.w()].doubleValue() )
return true;
}
}
return false;
}
// 返回图中是否有负权环
boolean negativeCycle(){
return hasNegativeCycle;
}
// 返回从s点到w点的最短路径长度
Number shortestPathTo( int w ){
assert w >= 0 && w < G.V();
assert !hasNegativeCycle;
assert hasPathTo(w);
return distTo[w];
}
// 判断从s点到w点是否联通
boolean hasPathTo( int w ){
assert( w >= 0 && w < G.V() );
return from[w] != null;
}
// 寻找从s到w的最短路径, 将整个路径经过的边存放在vec中
Vector<Edge<Weight>> shortestPath(int w){
assert w >= 0 && w < G.V() ;
assert !hasNegativeCycle ;
assert hasPathTo(w) ;
// 通过from数组逆向查找到从s到w的路径, 存放到栈中
Stack<Edge<Weight>> s = new Stack<Edge<Weight>>();
Edge<Weight> e = from[w];
while( e.v() != this.s ){
s.push(e);
e = from[e.v()];
}
s.push(e);
// 从栈中依次取出元素, 获得顺序的从s到w的路径
Vector<Edge<Weight>> res = new Vector<Edge<Weight>>();
while( !s.empty() ){
e = s.pop();
res.add(e);
}
return res;
}
// 打印出从s点到w点的路径
void showPath(int w){
assert( w >= 0 && w < G.V() );
assert( !hasNegativeCycle );
assert( hasPathTo(w) );
Vector<Edge<Weight>> res = shortestPath(w);
for( int i = 0 ; i < res.size() ; i ++ ){
System.out.print(res.elementAt(i).v() + " -> ");
if( i == res.size()-1 )
System.out.println(res.elementAt(i).w());
}
}
}Bellman-Ford算法的优化是利用队列数据结构完成,就是Queue-Based Bellman-Ford算法。
单源路径算法

所有对最短路径算法
Floyed算法,处理负权环的图,时间复杂度是O(V ^ 3)
最长路径算法
最长路径问题不能有正权环;无权图的最长路径问题是指数级难度的;对于有权图,不能使用Dijkstra求最长路径问题;可以使用Bellman-Ford算法。
























 2907
2907

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








