支持向量数据描述系列＜1＞

#1.目的

#2.困难

找到一个边界面包裹目标数据，使得边界内属于目标数据，边界外不属于目标数据，达到对目标数据的识别，本质上它是一种一分类分类器，能够对我和非我进行识别。
#3.解决方案
#4.效果

**

支持向量数据描述

**

摘要

数据描述是对训练目标数据进行描述，然后通过得到的数据描述判别新数据是否与训练数据相似。
我们的目的就是要找出这么一个函数描述目标数据。本文中这个函数是通过QP得到的一个球型边界面，球内的样本是目标数据，球外的样本是非目标数据。

1.引言
数据描述通过对目标训练样本进行训练，然后判断新样本是否与目标训练样本相似。
（1）用分类器的方法
如果新样本与训练样本相似，分类器才会得到可信的结果，未知区域样本的分类结果不可信。
要求提供与正常样本接近的非目标样本。
（2）用分布的方法
只注重于高密度区域，正常区域的分布很难描述
以上方法的困难在于当非目标样本难以获得时，以上方法很难实施。
（3）用边界面的方法描述
本文就是这个思路

2.理论
2.1正常的数据描述

SVDD与估计分类器的VC维比较类似，支持向量越多，VC维越复杂。
原始的优化问题为：


通过朗格朗日乘子法转变为对偶问题


C大于等于1，上式恒成立。

最终超球体的球心为样本的线性组合

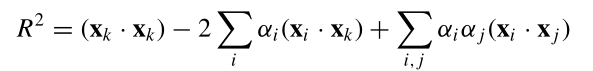
这个结果与SVC是类似的。

2.2加入负类样本
损失函数变为

通过朗格朗日乘子转变为对偶

加入负类样本后，部分负类样本可能变为支持向量。这个数据描述无法紧密的包裹目标数据

2.3灵活的描述
核函数的参数对SVDD的影响
线性核

远离原点的数据被认为是支持向量。
可以看到很多没有数据分布的区域被接受为目标区域。

高斯核

s越大，越接近于原始解。s越大，支持向量个数越少。
C越小，支持向量的个数越多。C越小，说明错了惩罚也很小导致更多的错误。C越小，超球体的体积越小。