前言
自学习基础整理,内容比较简单,结合理论基础和多篇博文、论文等做学习笔记如下,后文附参考博文和论文。
1.OFDM基础-时域理解
OFDM(Orthogonal Frequency Division Multiplexing)即正交频分复用技术,实际上OFDM是MCM(Multi Carrier Modulation),多载波调制的一种。通过频分复用实现高速串行数据的并行传输, 它具有较好的抗多径衰弱的能力,能够支持多用户接入。各子载波相互正交,所以扩频调制后的频谱可以相互重叠,不但减少了子载波间的相互干扰,还大大提高了频谱利用率。
OFDM主要思想是:将信道分成若干正交子信道,将高速数据信号转换成并行的低速子数据流,调制到在每个子信道上进行传输。正交信号可以通过在接收端采用相关技术来分开,这样可以减少子信道之间的相互干扰(ISI) 。每个子信道上的信号带宽小于信道的相关带宽,因此每个子信道上可以看成平坦性衰落,从而可以消除码间串扰,而且由于每个子信道的带宽仅仅是原信道带宽的一小部分,信道均衡变得相对容易。
在时域中,假设有信号 s i n ( t ) sin(t) sin(t)和 s i n ( 2 t ) sin(2t) sin(2t),如下图所示,其为正交, s i n ( t ) ∗ s i n ( 2 t ) sin(t)*sin(2t) sin(t)∗sin(2t)在 [ 0 , 2 π ] [0,2\pi] [0,2π]区间上的积分为0,在下面的图示中,在 [ 0 , 2 π ] [0,2\pi] [0,2π]的时长内,采用最易懂的幅度调制方式传送信号: s i n ( t ) sin(t) sin(t)传送信号 a a a,因此发送 a s i n ( t ) asin(t) asin(t),传送信号 b b b,因此发送 b s i n ( 2 t ) bsin(2t) bsin(2t)。
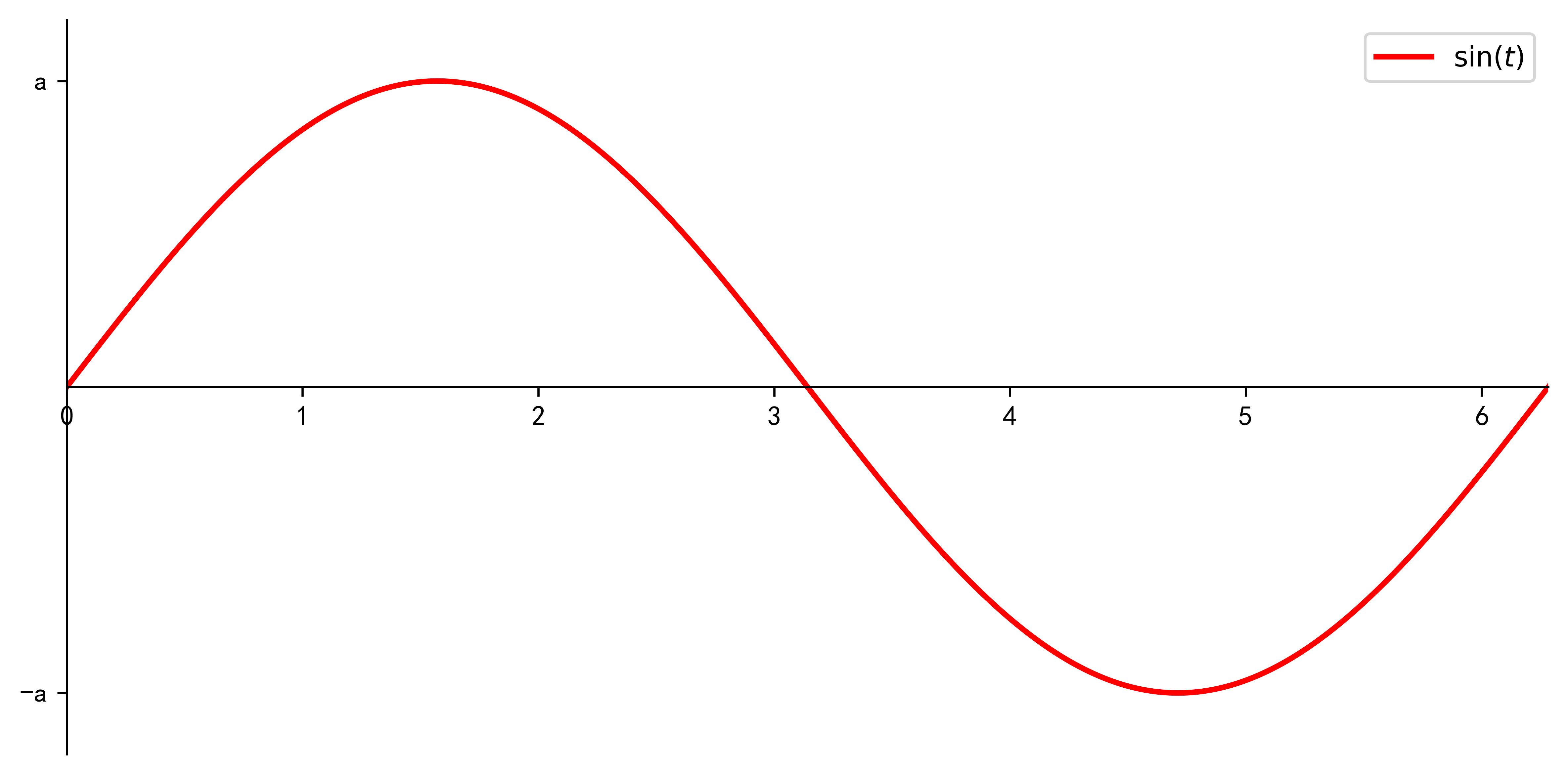
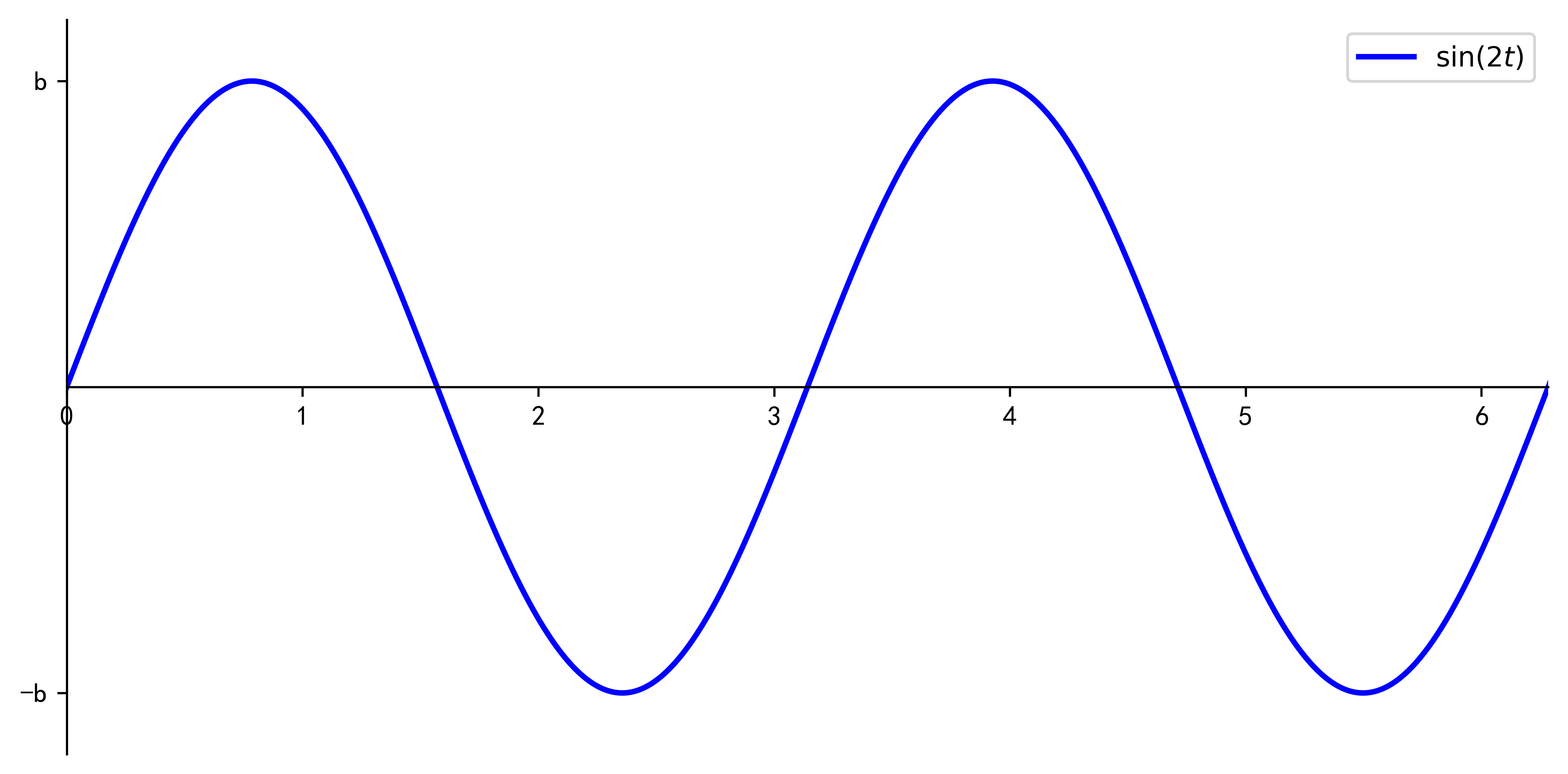
其中, s i n ( t ) sin(t) sin(t)和 s i n ( 2 t ) sin(2t) sin(2t)的用处是用来承载信号,是收发端预先规定好的信息,下文统一为子载波;调制在子载波上的幅度信号 a a a和 b b b,才是需要发送的信息。如下图为在信道中传送的信号为 a s i n ( t ) + b s i n ( 2 t ) asin(t)+bsin(2t) asin(t)+bsin(2t)。

在接收端,分别对接收到的信号作关于 s i n ( t ) sin(t) sin(t)和 s i n ( 2 t ) sin(2t) sin(2t)的积分检测,就可以得到 a a a和 b b b了。如下为接收信号乘 s i n ( t ) sin(t) sin(t),积分解码出








 本文详细介绍了OFDM(正交频分复用)技术的基础知识,包括时域理解,如OFDM的工作原理、符号间干扰和信道干扰的分析,以及ISI消除等。内容涵盖OFDM的实现步骤,如串并转换、调制解调、保护间隔、交织、信道编码等,并提及了多径效应和多径时延对OFDM系统的影响。
本文详细介绍了OFDM(正交频分复用)技术的基础知识,包括时域理解,如OFDM的工作原理、符号间干扰和信道干扰的分析,以及ISI消除等。内容涵盖OFDM的实现步骤,如串并转换、调制解调、保护间隔、交织、信道编码等,并提及了多径效应和多径时延对OFDM系统的影响。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1807
1807

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








