计算模型主要包括,图灵机、递归函数、λ演算、马尔科夫算法等。
图灵机
图灵机,又称确定型图灵机,是英国数学家阿兰·图灵于1936年提出的一种抽象计算模型,其更抽象的意义为一种数学逻辑机,可以看作等价于任何有限逻辑数学过程的终极强大逻辑机器。
图灵的基本思想[编辑]
图灵的基本思想是用机器来模拟人们用纸笔进行数学运算的过程,他把这样的过程看作下列两种简单的动作:
- 在纸上写上或擦除某个符号;
- 把注意力从纸的一个位置移动到另一个位置;
而在每个阶段,人要决定下一步的动作,依赖于(a)此人当前所关注的纸上某个位置的符号和(b)此人当前思维的状态。
为了模拟人的这种运算过程,图灵构造出一台假想的机器,该机器由以下几个部分组成:
- 一条无限长的纸带TAPE。纸带被划分为一个接一个的小格子,每个格子上包含一个来自有限字母表的符号,字母表中有一个特殊的符号
 表示空白。纸带上的格子从左到右依次被编号为0, 1, 2, ...,纸带的右端可以无限伸展。
表示空白。纸带上的格子从左到右依次被编号为0, 1, 2, ...,纸带的右端可以无限伸展。 - 一个读写头HEAD。该读写头可以在纸带上左右移动,它能读出当前所指的格子上的符号,并能改变当前格子上的符号。
- 一套控制规则TABLE。它根据当前机器所处的状态以及当前读写头所指的格子上的符号来确定读写头下一步的动作,并改变状态寄存器的值,令机器进入一个新的状态。
- 一个状态寄存器。它用来保存图灵机当前所处的状态。图灵机的所有可能状态的数目是有限的,并且有一个特殊的状态,称为停机状态。参见停机问题。
注意这个机器的每一部分都是有限的,但它有一个潜在的无限长的纸带,因此这种机器只是一个理想的设备。图灵认为这样的一台机器就能模拟人类所能进行的任何计算过程。
图灵机的正式定义[编辑]
一台图灵机是一个七元组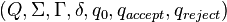 ,其中
,其中 都是有限集合,且满足
都是有限集合,且满足
 是状态集合;
是状态集合; 是输入字母表,其中不包含特殊的空白符
是输入字母表,其中不包含特殊的空白符 ;
; 为空白符;
为空白符; 是带字母表,其中
是带字母表,其中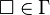 且
且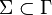 ;
;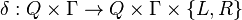 是转移函数,其中
是转移函数,其中 表示读写头是向左移还是向右移;
表示读写头是向左移还是向右移; 是起始状态;
是起始状态; 是接受状态。
是接受状态。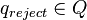 是拒绝状态,且
是拒绝状态,且 。
。
图灵机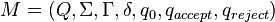 将以如下方式运作:
将以如下方式运作:
开始的时候将输入符号串  从左到右依此填在纸带的第
从左到右依此填在纸带的第 号格子上, 其他格子保持空白(即填以空白符
号格子上, 其他格子保持空白(即填以空白符 )。
)。  的读写头指向第0号格子,
的读写头指向第0号格子,  处于状态
处于状态 。 机器开始运行后,按照转移函数
。 机器开始运行后,按照转移函数 所描述的规则进行计算。 例如,若当前机器的状态为
所描述的规则进行计算。 例如,若当前机器的状态为 ,读写头所指的格子中的符号为
,读写头所指的格子中的符号为 , 设
, 设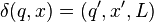 , 则机器进入新状态
, 则机器进入新状态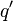 , 将读写头所指的格子中的符号改为
, 将读写头所指的格子中的符号改为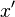 , 然后将读写头向左移动一个格子。 若在某一时刻,读写头所指的是第0号格子, 但根据转移函数它下一步将继续向左移,这时它停在原地不动。 换句话说,读写头始终不移出纸带的左边界。 若在某个时刻
, 然后将读写头向左移动一个格子。 若在某一时刻,读写头所指的是第0号格子, 但根据转移函数它下一步将继续向左移,这时它停在原地不动。 换句话说,读写头始终不移出纸带的左边界。 若在某个时刻 根据转移函数进入了状态
根据转移函数进入了状态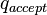 , 则它立刻停机并接受输入的字符串; 若在某个时刻
, 则它立刻停机并接受输入的字符串; 若在某个时刻 根据转移函数进入了状态
根据转移函数进入了状态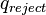 , 则它立刻停机并拒绝输入的字符串。
, 则它立刻停机并拒绝输入的字符串。
注意,转移函数 是一个部分函数, 换句话说对于某些
是一个部分函数, 换句话说对于某些 ,
, ,
,  可能没有定义, 如果在运行中遇到下一个操作没有定义的情况, 机器将立刻停机。
可能没有定义, 如果在运行中遇到下一个操作没有定义的情况, 机器将立刻停机。
图灵机的基本术语[编辑]
设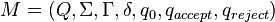 是一台图灵机,
是一台图灵机,
 的带描述(tape description)是一个函数
的带描述(tape description)是一个函数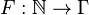 ,其中
,其中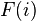 表示
表示 的带上第
的带上第 个格子中的符号;
个格子中的符号; 的格局(configuration)是一个三元组
的格局(configuration)是一个三元组 ,其中
,其中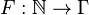 是当前的带描述,
是当前的带描述,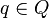 是当前的状态,
是当前的状态, 是当前读写头所处的位置;
是当前读写头所处的位置;- 设
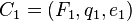 ,
, 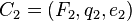 是
是 的格局,设
的格局,设 ,若满足
,若满足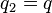 ,
,
以及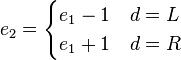
则称
 从格局
从格局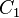 产生格局
产生格局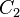 ,记作
,记作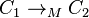 。
。 - 设
 为
为 的格局,若
的格局,若 则称
则称 为接受格局;若
为接受格局;若 则称
则称 为拒绝格局;接受格局和拒绝格局统称为停机格局。
为拒绝格局;接受格局和拒绝格局统称为停机格局。
设 是一台图灵机,将字符串
是一台图灵机,将字符串 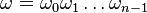 作为其输入,若存在格局序列
作为其输入,若存在格局序列 ,使得
,使得
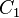 是
是 在输入
在输入 上的起始格局,即
上的起始格局,即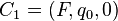 ,其中
,其中

 ,其中
,其中 ;
;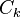 是接受格局。
是接受格局。
则称 接受字符串
接受字符串 ,且
,且 称为图灵机
称为图灵机 在输入
在输入 上的接受计算历史。同理,若
上的接受计算历史。同理,若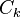 是拒绝格局,则称
是拒绝格局,则称 拒绝
拒绝 ,且
,且 称为图灵机
称为图灵机 在输入
在输入 上的拒绝计算历史。
上的拒绝计算历史。 所接受的所有字符串的集合称为
所接受的所有字符串的集合称为 的语言,记作
的语言,记作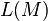 。
。
图灵机的例子[编辑]
设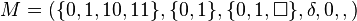
和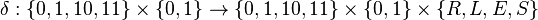 . 比如做一个以1的个数表示数值的加法运算, 在磁带上的数据是0000001110110000 , 就是3+2的意思。 程序
. 比如做一个以1的个数表示数值的加法运算, 在磁带上的数据是0000001110110000 , 就是3+2的意思。 程序 如下
如下
0,0 -> 0,0R
0,1 -> 1,1R
1,0 -> 10,1R
1,1 -> 1,1R
10,0 -> 11,0L
10,1 -> 10,1R
11,0 -> E
11,1 -> 0,0S
第一行程序0,0->0,0R意思就是如果机器读到0,就将其变成0,状态变为0,读写头向右移动一格. R就是向右移动一格,L就是向左移一格,E是错误,S是停机. xx,y -> aa,bb中xx是当前状态, y是当前格子的值, aa是程序下一步的状态, b是当前格的修改值.
虽然这里给出与上面不同形式的定义,但两者是等价的,这里的定义并不比上面的定义能完成更多的工作。
步数 状态 磁带 步数 状态 磁带
- - - - - - - - - - - - - - - - -
1 0 0000001110110000 9 1 0000001110110000
2 0 0000001110110000 10 1 0000001110110000
3 0 0000001110110000 11 10 0000001111110000
4 0 0000001110110000 12 10 0000001111110000
5 0 0000001110110000 13 10 0000001111110000
6 0 0000001110110000 14 11 0000001111110000
7 0 0000001110110000 15 0 0000001111100000(停机)
8 1 0000001110110000 -- 停机 --
通用图灵机[编辑]
对于任意一个图灵机,因为它的描述是有限的,因此我们总可以用某种方式将其编码为字符串。 我们用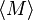 表示图灵机
表示图灵机 的编码。
的编码。
我们可以构造出一个特殊的图灵机,它接受任意一个图灵机 的编码
的编码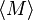 ,然后模拟
,然后模拟 的运作,这样的图灵机称为通用图灵机(Universal Turing Machine)。现代电子计算机其实就是这样一种通用图灵机,它能接受一段描述其他图灵机的程序,并运行程序实现该程序所描述的算法。
的运作,这样的图灵机称为通用图灵机(Universal Turing Machine)。现代电子计算机其实就是这样一种通用图灵机,它能接受一段描述其他图灵机的程序,并运行程序实现该程序所描述的算法。
图灵机的变体[编辑]
图灵机有很多变种,但可以证明这些变种的计算能力都是等价的,即它们识别同样的语言类。证明两个计算模型 和
和 的计算能力等价的基本思想是:用
的计算能力等价的基本思想是:用 和
和 相互模拟, 若
相互模拟, 若 可模拟
可模拟 且
且 可模拟
可模拟 ,显然他们的计算能力等价。注意这里我们暂时不考虑计算的效率,只考虑计算的理论上“可行性”。
,显然他们的计算能力等价。注意这里我们暂时不考虑计算的效率,只考虑计算的理论上“可行性”。
首先我们可以发现,改变图灵机的带字母表并不会改变其计算能力。例如我们可以限制图灵机的带字母表为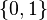 ,这并不会改变图灵机的计算能力,因为我们显然可以用带字母表为
,这并不会改变图灵机的计算能力,因为我们显然可以用带字母表为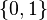 的图灵机模拟带字母表为任意有限集合
的图灵机模拟带字母表为任意有限集合 的图灵机。
的图灵机。
另一个要注意的是,如果我们允许图灵机的纸带两端都可以无限伸展,这并不能增加图灵机的计算能力,因为我们显然可以用只有纸带一端能无限伸展的图灵机来模拟这种纸带两端都可以无限伸展的图灵机。
如果我们允许图灵机的读写头在某一步保持原地不动,那也不会增加其计算能力,因为我们可以用向左移动一次再向右移动一次来代替在原地不动。
其它的常见图灵机变种包括:
图灵可计算性[编辑]
其它等价的计算模型[编辑]
除了图灵机以外,人们还发明了很多其它的计算模型。包括:
然而这些模型无一例外地都和图灵机的计算能力等价,因此邱奇,图灵和哥德尔 提出了著名的邱奇-图灵论题:一切直觉上能计算的函数都可用图灵机计算,反之亦然。
λ演算
λ演算(英语:lambda calculus,λ-calculus)是一套用于研究函数定义、函数应用和递归的形式系统。它由阿隆佐·邱奇和他的学生斯蒂芬·科尔·克莱尼在20世纪30年代引入。邱奇运用λ演算在1936年给出判定性问题(Entscheidungsproblem)的一个否定的答案。这种演算可以用来清晰地定义什么是一个可计算函数。关于两个lambda演算表达式是否等价的命题无法通过一个“通用的算法”来解决,这是不可判定性能够证明的头一个问题,甚至还在停机问题之先。Lambda演算对函数式编程语言有巨大的影响,比如Lisp语言、ML语言和Haskell语言。
Lambda演算可以被称为最小的通用程序设计语言。它包括一条变换规则(变量替换)和一条函数定义方式,Lambda演算之通用在于,任何一个可计算函数都能用这种形式来表达和求值。因而,它是等价于图灵机的。尽管如此,Lambda演算强调的是变换规则的运用,而非实现它们的具体机器。可以认为这是一种更接近软件而非硬件的方式。
本文讨论的是邱奇的“无类型lambda演算”,此后,已经研究出来了一些有类型lambda演算。
目录
[隐藏]历史[编辑]
最开始,邱奇试图创制一套完整的形式系统作为数学的基础,当他发现这个系统易受罗素悖论的影响时,就把lambda演算单独分离出来,用于研究可计算性,最终导致了他对判定性问题的否定回答。
非形式化的描述[编辑]
在λ演算中,每个表达式都代表一个函数,这个函数有一个参数,并且返回一个值。不论是参数和返回值,也都是一个单参的函数。可以这么说,λ演算中,只有一种“类型”,那就是这种单参函数。
函数是通过λ表达式匿名地定义的,这个表达式说明了此函数将对其参数进行什么操作。例如,“加2”函数f(x)= x + 2可以用lambda演算表示为λx.x + 2 (或者λy.y + 2,参数的取名无关紧要)而f(3)的值可以写作(λx.x + 2) 3。函数的应用(application)是左结合的:f x y =(f x) y。
考虑这么一个函数:它把一个函数作为参数,这个函数将被作用在3上:λf.f 3。如果把这个(用函数作参数的)函数作用于我们先前的“加2”函数上:(λf.f 3)(λx.x+2),则明显地,下述三个表达式:
- (λf.f 3)(λx.x+2) 与 (λx.x + 2) 3 与 3 + 2
是等价的。有两个参数的函数可以通过lambda演算这么表达:一个单一参数的函数的返回值又是一个单一参数函数的参数(参见Currying)。例如,函数f(x, y) = x - y可以写作λx.λy.x - y。下述三个表达式:
- (λx.λy.x - y) 7 2 与 (λy.7 - y) 2 与 7 - 2
也是等价的。然而这种lambda表达式之间的等价性无法找到一个通用的函数来判定。
并非所有的lambda表达式都可以规约至上述那样的确定值,考虑
- (λx.x x)(λx.x x)
或
- (λx.x x x)(λx.x x x)
然后试图把第一个函数作用在它的参数上。 (λx.x x)被称为ω 组合子,((λx.x x)(λx.x x))被称为Ω,而((λx.x x x) (λx.x x x))被称为Ω2,以此类推。
若仅形式化函数作用的概念而不允许lambda表达式,就得到了组合子逻辑。
形式化定义[编辑]
|
| 本条目包含过多行话或专业术语,可能需要简化或提出进一步解释。 |
形式化地,我们从一个标识符(identifier)的可数无穷集合开始,比如{a, b, c, ..., x, y, z, x1, x2, ...},则所有的lambda表达式可以通过下述以BNF范式表达的上下文无关文法描述:
- <表达式> ::= <标识符>
- <表达式> ::=(λ<标识符> .<表达式>)
- <表达式> ::=(<表达式> <表达式>)
头两条规则用来生成函数,而第三条描述了函数是如何作用在参数上的。通常,lambda抽象(规则2)和函数作用(规则3)中的括号在不会产生歧义的情况下可以省略。如下假定保证了不会产生歧义:(1)函数的作用是左结合的,和(2)lambda操作符被绑定到它后面的整个表达式。例如,表达式 (λx.x x)(λy.y) 可以简写成λ(x.x x) λy.y 。
类似λx.(x y)这样的lambda表达式并未定义一个函数,因为变量y的出现是自由的,即它并没有被绑定到表达式中的任何一个λ上。一个lambda表达式的自由变量的集合是通过下述规则(基于lambda表达式的结构归纳地)定义的:
- 在表达式V中,V是变量,则这个表达式里自由变量的集合只有V。
- 在表达式λV .E中(V是变量,E是另一个表达式),自由变量的集合是E中自由变量的集合减去变量V。因而,E中那些V被称为绑定在λ上。
- 在表达式 (E E')中,自由变量的集合是E和E'中自由变量集合的并集。
在lambda表达式的集合上定义了一个等价关系(在此用==标注),“两个表达式其实表示的是同一个函数”这样的直觉性判断即由此表述,这种等价关系是通过所谓的“alpha-变换规则”和“beta-归约规则”。
归约[编辑]
|
| 本条目包含过多行话或专业术语,可能需要简化或提出进一步解释。 |
α-变换[编辑]
Alpha-变换规则表达的是,被绑定变量的名称是不重要的。比如说λx.x和λy.y是同一个函数。尽管如此,这条规则并非像它看起来这么简单,关于被绑定的变量能否由另一个替换有一系列的限制。
Alpha-变换规则陈述的是,若V与W均为变量,E是一个lambda表达式,同时E[V:=W]是指把表达式E中的所有的V的自由出现都替换为W,那么在W不是 E中的一个自由出现,且如果W替换了V,W不会被E中的λ绑定的情况下,有
- λV.E == λW.E[V:=W]
这条规则告诉我们,例如λx.(λx.x) x这样的表达式和λy.(λx.x) y是一样的。
β-归约[编辑]
Beta-归约规则表达的是函数作用的概念。它陈述了若所有的E'的自由出现在E [V:=E']中仍然是自由的情况下,有
- ((λV.E) E') == E [V:=E']
成立。
==关系被定义为满足上述两条规则的最小等价关系(即在这个等价关系中减去任何一个映射,它将不再是一个等价关系)。
对上述等价关系的一个更具操作性的定义可以这样获得:只允许从左至右来应用规则。不允许任何beta归约的lambda表达式被称为Beta范式。并非所有的lambda表达式都存在与之等价的范式,若存在,则对于相同的形式参数命名而言是唯一的。此外,有一个算法用户计算范式,不断地把最左边的形式参数替换为实际参数,直到无法再作任何可能的规约为止。这个算法当且仅当lambda表达式存在一个范式时才会停止。Church-Rosser定理说明了,当且仅当两个表达式等价时,它们会在形式参数换名后得到同一个范式。
η-变换[编辑]
前两条规则之后,还可以加入第三条规则,eta-变换,来形成一个新的等价关系。Eta-变换表达的是外延性的概念,在这里外延性指的是,两个函数对于所有的参数得到的结果都一致,当且仅当它们是同一个函数。Eta-变换可以令λx .f x和f相互转换,只要x不是f中的自由出现。下面说明了为何这条规则和外延性是等价的:
若f与g外延地等价,即,f a == g a对所有的lambda表达式a成立,则当取a为在f中不是自由出现的变量x时,我们有f x == g x,因此λx .f x == λx .g x,由eta-变换f == g。所以只要eta-变换是有效的,会得到外延性也是有效的。
相反地,若外延性是有效的,则由beta-归约,对所有的y有(λx .f x) y == f y,可得λx .f x == f,即eta-变换也是有效的。
lambda演算中的算术[编辑]
在lambda演算中有许多方式都可以定义自然数,但最常见的还是邱奇数,下面是它们的定义:
-
0 = λf.λx.x -
1 = λf.λx.f x -
2 = λf.λx.f (f x) -
3 = λf.λx.f (f (f x))
以此类推。直观地说,lambda演算中的数字n就是一个把函数f作为参数并以f的n次幂为返回值的函数。换句话说,邱奇整数是一个高阶函数 -- 以单一参数函数f为参数,返回另一个单一参数的函数。
(注意在邱奇原来的lambda演算中,lambda表达式的形式参数在函数体中至少出现一次,这使得我们无法像上面那样定义0)在邱奇整数定义的基础上,我们可以定义一个后继函数,它以n为参数,返回n + 1:
-
SUCC = λn.λf.λx.f(n f x)
加法是这样定义的:
-
PLUS = λm.λn.λf.λx.m f (n f x)
PLUS可以被看作以两个自然数为参数的函数,它返回的也是一个自然数。你可以试试验证
-
PLUS 2 3
与5是否等价。乘法可以这样定义:
-
MULT = λm.λn.m(PLUS n)0,
即m乘以n等于在零的基础上n次加m。另一种方式是
-
MULT = λm.λn.λf.m(n f)
正整数n的前驱元(predecessesor)PRED n = n - 1要复杂一些:
-
PRED = λn.λf.λx.n(λg.λh.h(g f))(λu.x)(λu.u)
或者
-
PRED = λn.n(λg.λk.(g 1)(λu.PLUS(g k) 1) k)(λl.0) 0
注意(g 1)(λu.PLUS(g k) 1) k表示的是,当g(1)是零时,表达式的值是k,否则是g(k)+ 1。
逻辑与谓词[编辑]
习惯上,下述两个定义(称为邱奇布尔值)被用作TRUE和FALSE这样的布尔值:
- TRUE := λx.λy.x
-
FALSE := λx.λy.y
- (注意 FALSE等价于前面定义邱奇数零)
接着,通过这两个λ-项,我们可以定义一些逻辑运算:
- AND := λp q.p q FALSE
- OR := λp q.p TRUE q
- NOT := λp.p FALSE TRUE
- IFTHENELSE := λp x y.p x y
我们现在可以计算一些逻辑函数,比如:
-
AND TRUE FALSE
- ≡(λp q.p q FALSE) TRUE FALSE →β TRUE FALSE FALSE
- ≡(λx y.x) FALSE FALSE →β FALSE
我们见到AND TRUE FALSE等价于FALSE。
“谓词”是指返回布尔值的函数。最基本的一个谓词是ISZERO,当且仅当其参数为零时返回真,否则返回假:
- ISZERO := λn.n(λx.FALSE) TRUE
运用谓词与上述TRUE和FALSE的定义,使得"if-then-else"这类语句很容易用lambda演算写出。
有序对[编辑]
有序对(2-元组)数据类型可以用TRUE、FALSE和IF来定义。
- CONS := λx y.λp.IF p x y
- CAR := λx.x TRUE
- CDR := λx.x FALSE
链表数据类型可以定义为,要么是为空列表保留的值(e.g.FALSE),要么是CONS一个元素和一个更小的列表。
递归[编辑]
递归是使用函数自身的函数定义;在表面上,lambda演算不允许这样。但是这种印象是误解。考虑个例子,阶乘函数f(n)递归的定义为
- f(n):= if n = 0 then 1 else n·f(n-1)。
在lambda演算中,你不能定义包含自身的函数。要避免这样,你可以开始于定义一个函数,这里叫g,它接受一个函数f作为参数并返回接受n作为参数的另一个函数:
- g := λf n.(if n = 0 then 1 else n·f(n-1))。
函数g返回要么常量1,要么函数f对n-1的n次应用。使用ISZERO谓词,和上面描述的布尔和代数定义,函数g可以用lambda演算来定义。
但是,g自身仍然不是递归的;为了使用g来建立递归函数,作为参数传递给g的f函数必须有特殊的性质。也就是说,作为参数传递的f函数必须展开为调用带有一个参数的函数g -- 并且这个参数必须再次f函数!
换句话说,f必须展开为g(f)。这个到g的调用将接着展开为上面的阶乘函数并计算下至另一层递归。在这个展开中函数f将再次出现,并将被再次展开为g(f)并继续递归。这种函数,这里的f = g(f),叫做g的不动点,并且它可以在lambda演算中使用叫做悖论算子或不动点算子来实现,它被表示为Y -- Y组合子:
- Y = λg.(λx.g(x x))(λx.g(x x))
在lambda演算中,Y g是g的不动点,因为它展开为g(Y g)。现在,要完成我们对阶乘函数的递归调用,我们可以简单的调用 g(Y g)n,这里的n是我们要计算它的阶乘的数。
比如假定n = 5,它展开为:
- (λn.(if n = 0 then 1 else n·((Y g)(n-1)))) 5
- if 5 = 0 then 1 else 5·(g(Y g,5-1))
- 5·(g(Y g)4)
- 5·(λn.(if n = 0 then 1 else n·((Y g)(n-1))) 4)
- 5·(if 4 = 0 then 1 else 4·(g(Y g,4-1)))
- 5·(4·(g(Y g)3))
- 5·(4·(λn.(if n = 0 then 1 else n·((Y g)(n-1))) 3))
- 5·(4·(if 3 = 0 then 1 else 3·(g(Y g,3-1))))
- 5·(4·(3·(g(Y g)2)))
- ...
等等,递归的求值算法的结构。所有递归定义的函数都可以看作某个其他适当的函数的不动点,因此,使用Y所有递归定义的函数都可以表达为lambda表达式。特别是,我们现在可以明晰的递归定义自然数的减法、乘法和比较谓词。
可计算函数和lambda演算[编辑]
自然数的函数F: N → N是可计算函数,当且仅当存在着一个lambda表达式f,使得对于N中的每对x, y都有F(x) = y当且仅当f x == y,这里的x和y分别是对应于x和y的邱奇数。这是定义可计算性的多种方式之一;关于其他方式很它们的等价者的讨论请参见邱奇-图灵论题。
递归函数
在数理逻辑和计算机科学中,递归函数或μ-递归函数是一类从自然数到自然数的函数,它是在某种直觉意义上是"可计算的"。事实上,在可计算性理论中证明了递归函数精确的是图灵机的可计算函数。递归函数有关于原始递归函数,并且它们的归纳定义(见下)建造在原始递归函数之上。但是,不是所有递归函数都是原始递归函数—最著名的这种函数是阿克曼函数。
所有递归函数的集合叫做R。
定义[编辑]
μ-递归函数(或偏μ-递归函数)是接受自然数的有限元组并并返回一个单一自然数的偏函数。它们是包括初始函数并闭合在复合、原始递归和μ算子下的最小的偏函数类。
包括初始函数并闭合在复合和原始递归下的(就是说使用前五个函数定义的)最小的函数类是原始递归函数类。所有原始递归函数都是全函数。需要第六个或"μ算子"是因为不是所有全函数都可以只用五个原始递归函数来计算(比如阿克曼函数)。在这些实例中μ算子终止运算。它充当无界查找算子,无界但仍然(通过全函数定义)被某种方式(比如归纳证明)证明为最终生成一个数并终止运算。
但是,如果无界μ算子自身是偏函数 -- 就是说存在某个数它不能为其返回一个数 -- 使用它的函数将也是偏函数 -- 对某些数没有定义。在这些实例中,因为它是无界的,μ算子将永远查找,永不通过生成一个数而终止运算。(某些算法可以采用可以生成指示“不可判定”的符号"u"并以此终止运算的u-算子(cf Kleene (1952) pp. 328ff))。换句话说:使用偏μ算子的偏μ-递归函数可能不是全函数。全μ-递归函数的集合是全函数的偏μ-递归函数的子集。
前三个函数叫做"初始"或"基本"函数: ( Kleene (1952) p. 219):
-
- (1) 常数函数:对于每个自然数n和所有的k:
-
 。
。
-
- 有时这个常数通过重复使用后继函数和叫做"初始对象0 (零)"的对象来生成 (Kleene (1952) p.?)
-
- (2) 后继函数S: "从已经生成的对象到另一个对象n+1或n'(n的后继者)" (ibid)。
- S(x) ≡ def f(x) = x' = x +1
- (3) 投影函数Pik (也叫做恒等函数Iik ):对于所有自然数i使得
 :
:
-
P
i
k
 =
def
=
def
 .
.
- (4) 复合算子:复合也叫做代换,接受一个函数
 和函数
和函数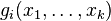 对每个i有
对每个i有 ,并返回映射x1, ... xk到
,并返回映射x1, ... xk到
-
 的一个函数。
的一个函数。
- (5) 原始递归算子:接受函数
 和
和 并返回唯一的函数
并返回唯一的函数 使得
使得
-
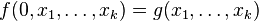 ,
,
-
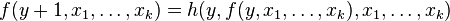 。
。
- (6) μ算子: μ算子接受一个函数
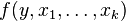 并返回函数
并返回函数 ,它的参数是x1 , . . ., xk。这个函数
,它的参数是x1 , . . ., xk。这个函数 要么是从自然数{ 0, 1, ... n }到自然数{ 0, 1, ... n }的数论函数,要么是运算于谓词(输出{ t, f })上生成{ 0, 1 }的表示函数。
要么是从自然数{ 0, 1, ... n }到自然数{ 0, 1, ... n }的数论函数,要么是运算于谓词(输出{ t, f })上生成{ 0, 1 }的表示函数。
-
在任何一个情况下:这个函数μ
y f返回最小的自然数
 使得,如果这样的
y存在,则
f(0,
x
1,
x
2,...,
x
k),
f(1,
x
1,
x
2,...,
x
k), ...,
f(
y,
x
1,
x
2,...,
x
k)都是有定义的,并且
f(
y,
x
1,
x
2,...,
x
k) = 0;如果这样的
y不存在,则μ
y f是对特定参数
x
1,...,
x
k是未定义的。
使得,如果这样的
y存在,则
f(0,
x
1,
x
2,...,
x
k),
f(1,
x
1,
x
2,...,
x
k), ...,
f(
y,
x
1,
x
2,...,
x
k)都是有定义的,并且
f(
y,
x
1,
x
2,...,
x
k) = 0;如果这样的
y不存在,则μ
y f是对特定参数
x
1,...,
x
k是未定义的。
强等于算子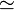 被用来比较偏μ-递归函数。这是对所有偏函数f和g定义的所以
被用来比较偏μ-递归函数。这是对所有偏函数f和g定义的所以
成立,当且仅当对于参数的任何选择要么两个函数都有定义并且它们的值相等要么两个函数都是未定义的。
同其他模型的等价性[编辑]
在可计算性模型的等价中在对特定输入不终止的图灵机和对这个输入得到未定义结果的相应偏递归函数之间是平行/并列的。无界查找运算是不能通过原始递归的规则定义的,因为它们不提供"无限循环"(未定义值)的机制。
范式定理[编辑]
范式定理源于Kleene声称对于每个k有原始递归函数 和
和 使得对于任何k个自由变量的μ-递归函数
使得对于任何k个自由变量的μ-递归函数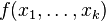 有一个e使得
有一个e使得
-
 。
。
数e被叫做函数f的索引或哥德尔数。这个结果的一个结论是任何μ-递归函数都可以使用把μ算子应用于(全)原始递归函数的一个单一实例来定义。
Minsky (1967)(同样Boolos-Burgess-Jeffrey (2002) pp. 94-95)观察到上面定义的U在本质上是通用图灵机的μ-递归等价物:
- “要构造U就是写下通用递归函数U(n, x)的定义,它正确的解释数n并计算x的适当的函数。要直接构造U涉及与我们在构造通用图灵机的研究中本质上同量的努力, 和本质上同样的想法” (italics in original, Minsky (1967) p. 189)。
邱奇-图灵论题
邱奇-图灵论题(邱奇-图灵猜想,邱奇论题,邱奇猜想,图灵论题)是一个关于可计算性理论的假设。该假设论述了关于函数特性的,可有效计算的函数值(用更现代的表述来说--在算法上可计算的)。简单来说,邱奇-图灵论题认为“任何在算法上可计算的问题同样可由图灵机计算”。是
20世纪上半叶,对可计算性进行公式化表示的尝试有:
- 美国数学家阿隆佐·邱奇创建了称为λ演算的方法来定义函数
- 英国数学家阿兰·图灵创建了可对输入进行运算的理论机器模型,现在被称为通用图灵机
- 邱奇以及数学家斯蒂芬·科尔·克莱尼和逻辑学家J.B. Rosser一起定义了一类函数, 这种函数的值可使用递归方法计算
这三个理论在直觉上似乎是等价的--它们都定义了同一类函数。因此,计算机科学家和数学家们相信,可计算性的精确定义已经出现。邱奇-图灵论题的非正式表述说:如果某个算法是可行的,那这个算法同样可以被图灵机,以及另外两个理论所实现。
虽然这三个理论被认为三是等价的,但是其中的前提假设--“能够有效计算”是一个模糊的定义。因此,虽然这个假说已接近完全,但仍然不能由公式证明。
假说前提[编辑]
已知的三种计算过程(递归,λ演算和图灵机)都是等价的--这三种方法定义了同一类函数。这导致数学家和计算机科学家相信可计算性的概念可由上述三种等价的计算过程描述。简单来讲,邱奇-图灵论题认为如果某种方法(算法)可进行运算,那么该运算也可被图灵机执行(也可被递归定义的函数或λ函数执行)。
邱奇-图灵论题是对计算特性进行描述的一种陈述,故而不能被严格证明。虽然上面提到的三种计算过程可被证明为等价的,但是邱奇-图灵论题最根本的前提--声称一个函数是“可有效计算的”究竟意味着什么--在某种意义上是不甚明确的直觉结果。所以,该论题依然是一个假想。
尽管邱奇-图灵论题不能被证明,到目前为止它仍然受到近乎全面的接受。
正式阐述[编辑]
Rosser于1939年对“可有效计算性”进行了如下的解读:“很明显CC和RC(邱奇和Rosser的论据)的成立依赖于对‘有效性’的严格定义。‘有效的方法’主要是指该方法的每一步都可被事先确定,而且该方法可在有限的步数之内生成结果”。因此,‘有效性’实际上包含两层含义:
- 产生一种确定的,或者所需的效果
- 能够产生计算结果
接下来, 术语“可有效演算的”意味着“由任何直观上有效的方法产生的”,而术语“可有效计算的”意味着“由图灵机或任何等价的机械设备产生的”。图灵本人对此的定义由他在1939年的博士论文“基于有序数的逻辑系统”的脚注中给出:
- “ †我们应该使用‘可计算函数’来表示一个可被机器计算的函数, 使用‘可有效演算的’来指代那些并未特别指明的直观想法。”
这可以转述如下:
- 任何可有效演算的函数都是可计算函数。
图灵则是如此描述的:
- “当一个函数的值可由某种纯机械计算步骤得到时, 它就是可有效演算的函数...应该这样认识: 可计算性和可有效演算性是不同的。”
等价形式[编辑]
本论题的另外一种说法就是逻辑和数学中的有效或机械方法可由图灵机来表示。通常我们假定这些方法必须满足以下的要求:
- 一个方法由有限多简单和精确的指令组成,这些指令可由有限多的符号来描述。
- 该方法总会在有限的步骤内产生出一个结果。
- 基本上人可以仅用纸张和铅笔来执行。
- 该方法的执行不需人类的智慧来理解和执行这些指令。
此类方法的一个范例便是用于确定两个自然数的最大公约数的欧基里德算法。
“有效方法”这个想法在直觉上是清楚的,但却没有在形式上加以定义,因为什么是“一个简单而精确的指令”和什么是“执行这些指令所需的智力”这两个问题并没有明确的答案。(如需欧几里得算法之外的范例,请参见数论中的有效结果。)
起源[编辑]
在他1936年的论文“论可计算数字,及其在判定性问题(德语:Entscheidungsproblem)中的应用”中,阿兰·图灵试图通过引入图灵机来形式地展示这一想法。在此篇论文中,他证明了“判定性问题”是无法解决的。几个月之前,阿隆佐·邱奇在“关于判定性问题的解释”(A Note on the Entscheidungsproblem)一文中证明出了一个相似的论题,但是他采用递归函数和Lambda可定义函数来形式地描述有效可计算性。Lambda可定义函数由阿隆佐·邱奇和斯蒂芬·克莱尼(Church 1932, 1936a, 1941, Kleene 1935)提出,而递归函数由库尔特·哥德尔(Kurt Gödel)和雅克斯·赫尔不兰特(Jacques Herbrand,Gödel 1934, Herbrand 1932)提出。这两个机制描述的是同一集合的函数,正如邱奇和克林(Church 1936a, Kleene 1936)所展示的正整数函数那样。在听说了邱奇的建议后,图灵很快就证明了他的图灵机实际上描述的是同一集合的函数(Turing 1936, 263ff).y
影响[编辑]
之后用于描述有效计算的许多其他机制也被提了出来,比如寄存器机、埃米尔·波斯特(Emill Post)的波斯特系统,组合子逻辑以及马尔可夫算法(Markov 1960)等。所有这些体系都已被证明在计算上和图灵机拥有基本相同的能力;类似的系统被称为图灵完全。因为所有这些不同的试图描述算法的努力都导致了等价的结果,所以现在普遍认为邱奇-图灵论题是正确的。但是,该论题不具有数学定理一般的地位,也无法被证明;说是定理不如说是个将可计算性等同于图灵机的提议。如果能有一个方法能被普遍接受为一个有效的算法但却无法在图灵机上允许,则该论题也是可以被驳斥的。
在20世纪初期,数学家们经常使用一种非正式的说法即可有效计算,所以为这个概念寻找一个好的形式描述也是十分重要的。当代的数学家们则使用图灵可计算(或简写为可计算)这一定义良好的概念。由于这个没有定义的用语在使用中已经淡去,所以如何定义它的问题已经不是那么重要了。
哲学内涵[编辑]
邱奇-图灵论题对于心智哲学(philosophy of mind)有很多寓意,但是对于该论题的很多哲学解读存在曲解。哲学学者B. Jack Copeland认为关于图灵机是否可模拟确定的物理过程的问题仍没有得到解答。他进一步声称关于这些物理过程是否在人类的智能机制中起到作用的问题也是未决的。有很多重要而悬而未决的问题也涵盖了邱奇-图灵论题和物理学及超计算(hypercomputation)的可能性之间的关系。应用到物理学上,该论题有很多可能的意义:
- 宇宙是一台图灵机(由此,在物理上对非递归函数的计算是不可能的)。该论述被定义为大邱奇-图灵论题。
- 宇宙不是一台图灵机(也就是说,物理的定律不是图灵可计算的),但是不可计算的物理事件却不能阻碍创建超计算机(hypercomputer)的可能性。比如,一个在物理上包含实数而非可计算实数的宇宙就可以被划为此类。
- 宇宙是一台超计算机,而且建造物理设备来实现这一特性并以之计算非递归函数是可能的。比如,一个悬而未决的问题是我们无法确定量子力学(quantum mechanical)的事件是否图灵可计算的,尽管诸如量子图灵机之类的严格模型实际上等价于确定性图灵机(但并不一定在效率上等价)。约翰·卢卡斯和名气更大一点的罗格·本罗泽(Roger Penrose)曾经建议说人的心灵可能是量子力学和非算法计算的结果, 尽管并没有科学证据支持这一提议。
实际上在这三类之外或其中还有许多其他的技术上的可能性,但这三类只是为了阐述这一概念。
不可计算函数[编辑]
我们可以正式定义不可计算的函数。一个有名的例子是海狸很忙(Busy Beaver)函数。该函数接受输入n,返回具有n个状态的图灵机在停机之前所能打印的最大符号数量。找到海狸很忙函数的上限等价于解决停机问题,该问题已被确定不能使用图灵机解决。由于海狸很忙函数不能被图灵机计算, 邱奇-图灵论题断言该函数不能使用任何方法进行有效计算。更多信息可参考文章Busy Beaver。
存在一些模型可用于计算(邱奇-图灵)不可计算函数:即所谓的超计算机。Mark Burgin认为类似归纳性图灵机的超递归算法(super-recursive algorithms)可用于反证邱奇-图灵论题。他的论述依赖于对算法更广泛的定义, 这种定义上的扩展使得一些归纳性图灵机包含的不可计算函数变得可计算。这种对邱奇-图灵论题的解读与计算机科学的常规解读不同,把超递归算法归于邱奇-图灵意义上的算法的这种看法并未受到相关领域的广泛接受。
参考文献:维基百科
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








