矩阵的特征值和特征向量是线性代数以及矩阵论中非常重要的一个概念。在遥感领域也是经常用到,比如多光谱以及高光谱图像的主成分分析要求解波段间协方差矩阵或者相关系数矩阵的特征值和特征向量。
根据普通线性代数中的概念,特征值和特征向量可以用传统的方法求得,但是实际项目中一般都是用数值分析的方法来计算,这里介绍一下雅可比迭代法求解特征值和特征向量。
雅克比方法用于求实对称阵的全部特征值、特征向量。
对于实对称阵 A,必有正交阵 U,使
U TA U = D。
其中 D 是对角阵,其主对角线元 li 是 A 的特征值. 正交阵 U 的第 j 列是 A 的属于 li 的特征向量。
原理:Jacobi 方法用平面旋转对矩阵 A 做相似变换,化A 为对角阵,进而求出特征值与特征向量。
既然用到了旋转,这里就介绍一下旋转矩阵。
对于 p ≠ q,下面定义的 n 阶矩阵Upq 是平面旋转矩阵。
容易验证 Upq是正交阵。对于向量x,Upq x 相当于把坐标轴Oxp和 Oxq 于所在的平面内旋转角度 j .
变换过程: 在保证相似条件下,使主对角线外元素趋于零!
记 n 阶方阵A = [aij], 对 A 做下面的变换:
A1= UpqTAUpq,
A1 仍然是实对称阵,因为,UpqT =Upq-1,知A1与 A 的特征值相同。
前面说了雅可比是一种迭代算法,所以每一步迭代时,需要求出旋转后新的矩阵,那么新的矩阵元素如何求,这里给出具体公式如下:
由上面的一组公式可以看到:
(1)矩阵A1 的第p 行、列与第 q 行、列中的元素发生了变化,其它行、列中的元素不变。
(2)p、q分别是前一次的迭代矩阵A的非主对角线上绝对值最大元素的行列号
(3) j是旋转角度,可以由下面的公式计算:
归纳可以得到雅可比迭代法求解矩阵特征值和特征向量的具体步骤如下:
(1) 初始化特征向量为对角阵V,即主对角线的元素都是1.其他元素为0。
(2) 在A的非主对角线元素中,找到绝对值最大元素 apq 。
(3) 用式(3.14)计算tan2j,求 cosj, sinj 及矩阵Upq .
(4) 用公式(1)-(4)求A1;用当前特征向量矩阵V乘以矩阵Upq得到当前的特征向量V。
(5) 若当前迭代前的矩阵A的非主对角线元素中最大值小于给定的阈值e时,停止计算;否则, 令A = A1 , 重复执行(2) ~ (5)。 停止计算时,得到特征值 li≈(A1) ij ,i,j= 1,2,…,n.以及特征向量V。
(6) 这一步可选。根据特征值的大小从大到小的顺序重新排列矩阵的特征值和特征向量。
到现在为止,每一步的计算过程都十分清楚了,写出代码也就不是难事了,具体代码如下:
/**
* @brief 求实对称矩阵的特征值及特征向量的雅克比法
* 利用雅格比(Jacobi)方法求实对称矩阵的全部特征值及特征向量
* @param pMatrix 长度为n*n的数组,存放实对称矩阵
* @param nDim 矩阵的阶数
* @param pdblVects 长度为n*n的数组,返回特征向量(按列存储)
* @param dbEps 精度要求
* @param nJt 整型变量,控制最大迭代次数
* @param pdbEigenValues 特征值数组
* @return
*/
bool CPCAAlg::JacbiCor(double * pMatrix,int nDim, double *pdblVects, double *pdbEigenValues, double dbEps,int nJt)
{
for(int i = 0; i < nDim; i ++)
{
pdblVects[i*nDim+i] = 1.0f;
for(int j = 0; j < nDim; j ++)
{
if(i != j)
pdblVects[i*nDim+j]=0.0f;
}
}
int nCount = 0; //迭代次数
while(1)
{
//在pMatrix的非对角线上找到最大元素
double dbMax = pMatrix[1];
int nRow = 0;
int nCol = 1;
for (int i = 0; i < nDim; i ++) //行
{
for (int j = 0; j < nDim; j ++) //列
{
double d = fabs(pMatrix[i*nDim+j]);
if((i!=j) && (d> dbMax))
{
dbMax = d;
nRow = i;
nCol = j;
}
}
}
if(dbMax < dbEps) //精度符合要求
break;
if(nCount > nJt) //迭代次数超过限制
break;
nCount++;
double dbApp = pMatrix[nRow*nDim+nRow];
double dbApq = pMatrix[nRow*nDim+nCol];
double dbAqq = pMatrix[nCol*nDim+nCol];
//计算旋转角度
double dbAngle = 0.5*atan2(-2*dbApq,dbAqq-dbApp);
double dbSinTheta = sin(dbAngle);
double dbCosTheta = cos(dbAngle);
double dbSin2Theta = sin(2*dbAngle);
double dbCos2Theta = cos(2*dbAngle);
pMatrix[nRow*nDim+nRow] = dbApp*dbCosTheta*dbCosTheta +
dbAqq*dbSinTheta*dbSinTheta + 2*dbApq*dbCosTheta*dbSinTheta;
pMatrix[nCol*nDim+nCol] = dbApp*dbSinTheta*dbSinTheta +
dbAqq*dbCosTheta*dbCosTheta - 2*dbApq*dbCosTheta*dbSinTheta;
pMatrix[nRow*nDim+nCol] = 0.5*(dbAqq-dbApp)*dbSin2Theta + dbApq*dbCos2Theta;
pMatrix[nCol*nDim+nRow] = pMatrix[nRow*nDim+nCol];
for(int i = 0; i < nDim; i ++)
{
if((i!=nCol) && (i!=nRow))
{
int u = i*nDim + nRow; //p
int w = i*nDim + nCol; //q
dbMax = pMatrix[u];
pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta;
pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta;
}
}
for (int j = 0; j < nDim; j ++)
{
if((j!=nCol) && (j!=nRow))
{
int u = nRow*nDim + j; //p
int w = nCol*nDim + j; //q
dbMax = pMatrix[u];
pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta;
pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta;
}
}
//计算特征向量
for(int i = 0; i < nDim; i ++)
{
int u = i*nDim + nRow; //p
int w = i*nDim + nCol; //q
dbMax = pdblVects[u];
pdblVects[u] = pdblVects[w]*dbSinTheta + dbMax*dbCosTheta;
pdblVects[w] = pdblVects[w]*dbCosTheta - dbMax*dbSinTheta;
}
}
//对特征值进行排序以及重新排列特征向量,特征值即pMatrix主对角线上的元素
std::map<double,int> mapEigen;
for(int i = 0; i < nDim; i ++)
{
pdbEigenValues[i] = pMatrix[i*nDim+i];
mapEigen.insert(make_pair( pdbEigenValues[i],i ) );
}
double *pdbTmpVec = new double[nDim*nDim];
std::map<double,int>::reverse_iterator iter = mapEigen.rbegin();
for (int j = 0; iter != mapEigen.rend(),j < nDim; ++iter,++j)
{
for (int i = 0; i < nDim; i ++)
{
pdbTmpVec[i*nDim+j] = pdblVects[i*nDim + iter->second];
}
//特征值重新排列
pdbEigenValues[j] = iter->first;
}
//设定正负号
for(int i = 0; i < nDim; i ++)
{
double dSumVec = 0;
for(int j = 0; j < nDim; j ++)
dSumVec += pdbTmpVec[j * nDim + i];
if(dSumVec<0)
{
for(int j = 0;j < nDim; j ++)
pdbTmpVec[j * nDim + i] *= -1;
}
}
memcpy(pdblVects,pdbTmpVec,sizeof(double)*nDim*nDim);
delete []pdbTmpVec;
return 1;
}








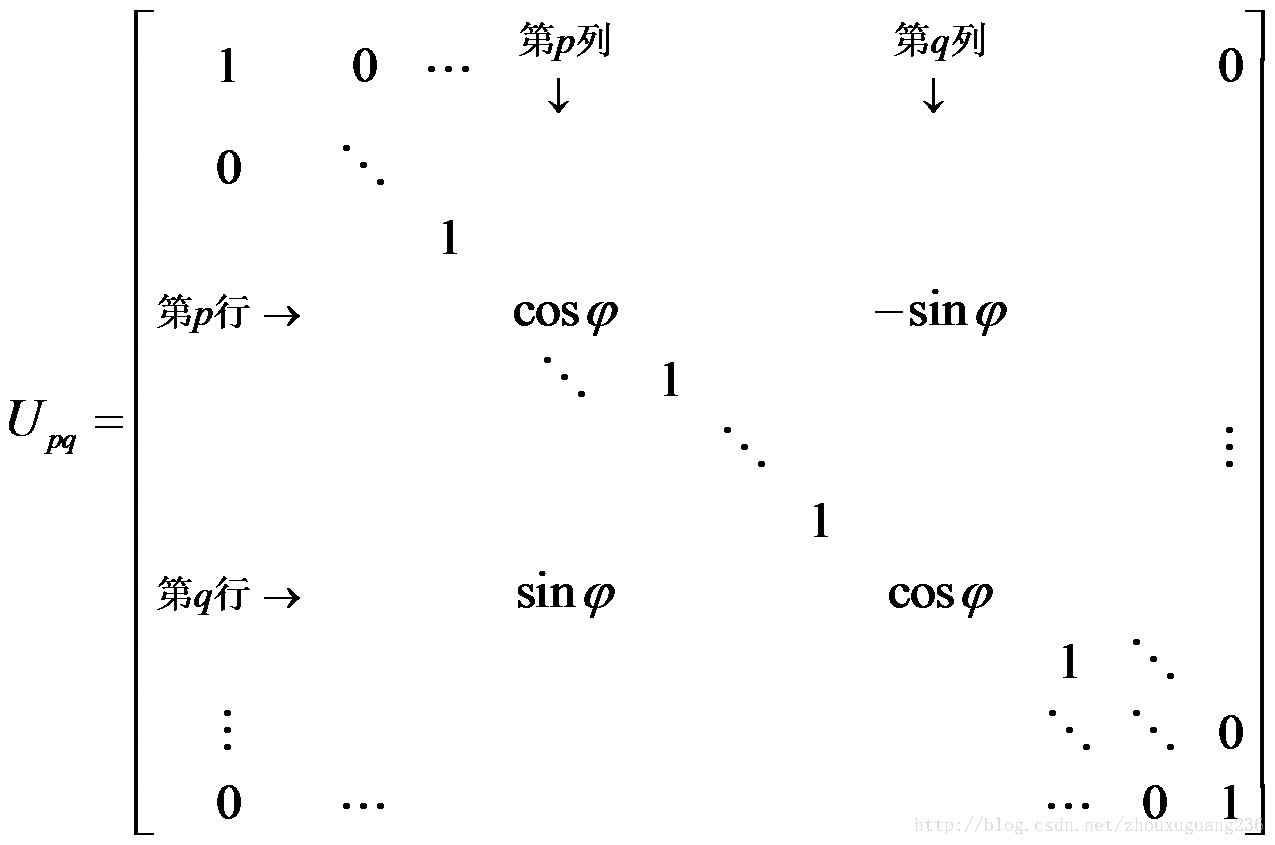
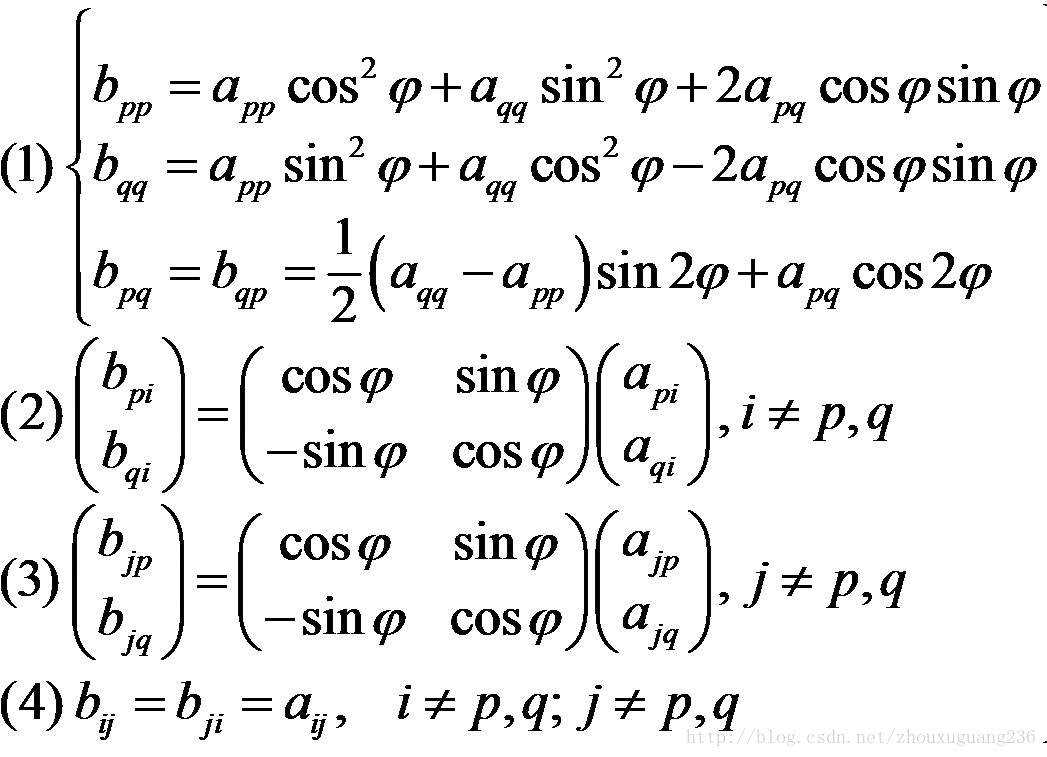
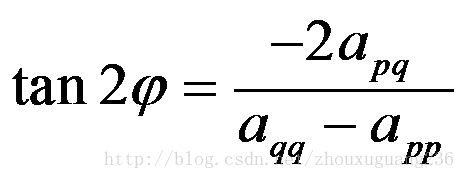














 5531
5531











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








