圆的Bresenham算法的opengL实现

源代码实现如下：

// Bresenham_circile.cpp : 定义控制台应用程序的入口点。
//


#include "stdafx.h"
#include<stdlib.h>
#include <GL/glut.h>

/* initialization: */
void myinit(void)
{
 
/* attributes */

      glClearColor(1.0, 1.0, 1.0, 0.0); /* white background */
      glColor3f(1.0, 0.0, 0.0); /* draw in red */

/* set up viewing: */
/* 500 x 500 window with origin lower left */

      glMatrixMode(GL_PROJECTION);
      glLoadIdentity();
      gluOrtho2D(0.0, 500.0, 0.0, 500.0);
      glMatrixMode(GL_MODELVIEW);
}
void  plot_circle_points(int xc,int yc,int x,int y)
{
      glBegin(GL_POINTS);
      glVertex3f(xc+x,yc+y,0); 
      glVertex3f(xc-x,yc+y,0);
      glVertex3f(xc+x,yc-y,0);
      glVertex3f(xc-x,yc-y,0);
      glVertex3f(xc+y,yc+x,0);
      glVertex3f(xc-y,yc+x,0);
      glVertex3f(xc+y,yc-x,0);
      glVertex3f(xc-y,yc-x,0);
      glEnd();     
}
void drawcircle(int xc,int yc,int radius)
{
     int x,y,p;
     x=0;
     y=radius;
     p=3-2*radius;
     glClear(GL_COLOR_BUFFER_BIT);
     glBegin(GL_POINTS);
     while(x<y)
     {
          plot_circle_points(xc,yc,x,y);
          if(p<0)
                 p=p+4*x+6;
          else
          {
                 p=p+4*(x-y)+10;
                 y-=1;                 
          }
          x+=1;          
     }     
     if(x==y)
          plot_circle_points(xc,yc,x,y);
}


/* the display callback: */
void display( void )
{
    glClear(GL_COLOR_BUFFER_BIT);  /*clear the window */

    /*----------------------------------------*/
    /*  viewport stuff                        */
    /*----------------------------------------*/
    /* set up a viewport in the screen window */
    /* args to glViewport are left, bottom, width, height */
    glViewport(0, 0, 500, 500);
    /* NB: default viewport has same coords as in myinit, */
    /* so this could be omitted: */

    
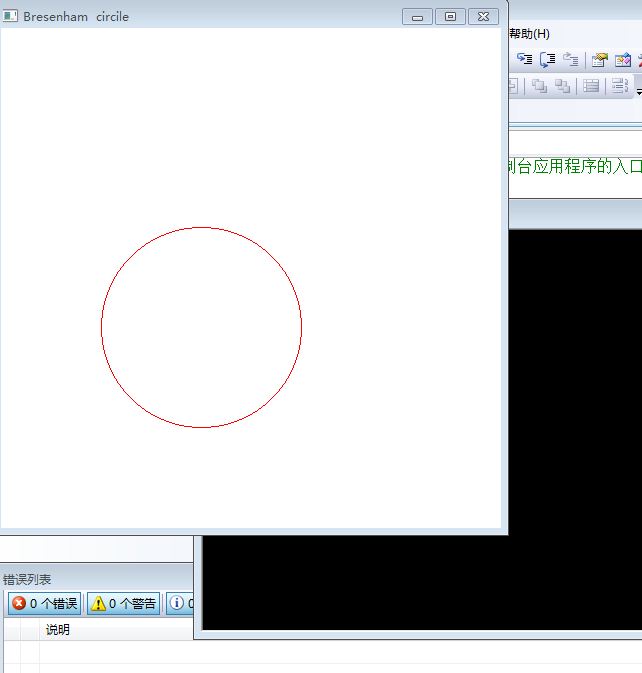
  drawcircle(200,200,100);

    /* and flush that buffer to the screen */
    glFlush(); 
 }

int main(int argc, char** argv)
{

/* Standard GLUT initialization */

    glutInit(&argc,argv);
    glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB); /* default, not needed */
    glutInitWindowSize(500,500); /* 500 x 500 pixel window */
    glutInitWindowPosition(0,0); /* place window top left on display */
    glutCreateWindow("Bresenham  circile"); /* window title */
    glutDisplayFunc(display); /* display callback invoked when window opened */
     myinit(); /* set attributes */
    glutMainLoop(); /* enter event loop */
}

 

 

 

 设要显示圆的圆心在原点(0，0)，半径为R，初始点的坐标为(0，R)，顺时针生成八分之一圆，令：F(x，y)=x²+y²-R²

则圆的方程为：

F(x，y)=0

(2-27)

当点(x，y)在圆内时，则F(x，y)<0；
当点(x，y)在圆外时，则F(x，y)>0；
当点(x，y)在圆上时，则F(x，y)=0；

现以下图的AB弧为例，来说明正负画圆法(顺时针生成圆)。

　　假设当前点为P_i(x_i，y_i)，取下一个点P_i+1(x_i+1，y_i+1)的原则是：
　　1、当F(x_i，y_i)≤0时：取x_i+1= x_i+1，y_i+1= y_i。即向右走一步，从圆内走向圆外。对应图(a)中的从P_i到P_i+1。
　　2、当F(x_i，y_i)>0时：取x_i+1= x_i，y_i+1= y_i-1。即向下走一步，从圆外走向圆内。对应图(b)中的从P_i到P_i+1。

　　由于向圆内或向圆外走取决于F(x_i，y_i)的正负，因此称为正负法。

　　下面分两种情况求出F(x_i，y_i)的递推公式：
　　(1) 当F(x_i，y_i)≤0时，向右走，取x_i+1=x_i+1，y_i+1=y_i，则

F(x i+1，y i+1)

= F(x i+1，y i) =(x i+1) 2+y i 2- R 2 =(x i 2+y i 2- R 2)+2x i+1 = F(x i，y i)+2x i+1

(2-28)

　　(2) 当F(x_i，y_i)>0时，向下走，取x_i+1=x_i，y_i+1=y_i-1，则

F(x i+1，y i+1)

= F(x i，y i-1) =x i 2+(y i-1) 2- R 2 =(x i 2+y i 2- R 2)-2y i+1 = F(x i，y i)-2y i+1

(2-29)

　　初始时，x=0，y=R，故

F(0，R)=(02+R2)-R2=0

(2-30)

　　公式(2-28)、(2-29)和(2-30)就构成正负画圆算法的核心。

　　给象素坐标(x，y)及F赋初始值后，进入循环画点；

　　画点后，根据F的符号进行F值的递推和下一个点的获取，直到x>y为止。

　　同前面介绍的一样，利用圆的八分对称性，循环一次，画八个点。

注意：初值不同、圆的生成方向不同时，当前点和下一个点的获取原则是不同的，见下图。

　　例如，初始点(R，0)，逆时针生成圆，从图（b）可知：

　　若当前点P_i在圆内，则下一点P_i+1(x_i，y_i+1)，即向上走一步；
　　若当前点P_i在圆外，则下一点P_i+1(x_i-1，y_i)，即向左走一步；

(a) 顺时针生成圆　　　 　　　　(b) 逆时针生成圆

 

// 顺时针生成圆
void PNARC(int x0,int y0,int r,int color)
{
　int x=0,y=r,f=0;
　while(x<=y)
　{
　　putdot(x0,y0,x,y,color);
　　if(f<=0)
　　{
　　　f=f+2*x+1;
　　　x++;
　　}
　　else
　　{
　　　f=f-2*y+1;
　　　y--;
　　}
　}
}