PTA 03-树3 Tree Traversals Again 最优解法——实时输出法分析

PTA-mooc完整题目解析及AC代码库：PTA（拼题A）-浙江大学中国大学mooc数据结构全AC代码与题目解析（C语言）

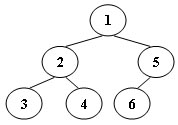
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: “Push X” where X is the index of the node being pushed onto the stack; or “Pop” meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop     
    

Sample Output:

3 4 2 6 5 1

题目解析

输入分析

第一行给出树的结点个数N，后面2*N行给出具体的对于该树的入栈、出栈访问过程

输出分析

输出给定树结构的后序遍历序列

解法分析

网上大多数做法有两种：

1. 根据前序和中序遍历序列求出后序遍历序列；
2. 构建一棵完整的树，然后利用中序遍历序列来求

这里我没有使用这两种做法，而是只使用一个栈结构，在读入入栈和出栈的操作过程时，实时输出后序序列。

关键点分析

非递归输出后序遍历序列时，因为父节点是最后输出的，因此在其输出时它的右子节点一定已经输出完毕，但在访问时为了访问到它的右子结点，已经将父节点出栈，所以这里产生了一个问题：当输出右子节点后，再想要输出的父节点已经出栈，访问不到了

因此为了解决这个问题有两种做法：

1. 为每一个结点增加一个变量域用来标识其是否为父节点
2. 将每一个父节点存入到另一个临时栈中（较复杂）

因为第二种方法还需判断临时栈中的每一个父节点与现有栈出栈的元素是否为父子关系，故需使用额外变量域表示这种联系，实现较为麻烦，因此此处使用第一种方法

算法思路

实际该题思路非常简单，使用一个栈模拟该树访问的入栈、出栈顺序即可。每一个结点都有一个father变量域来标识是否为父节点

判断某个结点是否为父节点的方法是：当Pop该结点时，后一条操作是Push，则说明Pop出来的结点为父节点，后一个要Push的结点为其右孩子

因此，可分为三种情况：

1. 遇到Push操作，直接push该元素
2. 遇到Pop操作，若下一条是Push命令，则Pop出该元素后，将其father标识为1，然后重新Push进栈中
3. 遇到Pop操作，若下一条是Pop命令，则Pop出该元素后，还需判断此时栈顶元素是不是其父节点，即此时的栈顶元素的father是否为1，然后将此时所有在栈顶的父节点已经出栈输出

---

Talk is cheap, show me the code.（废话不多说，上代码）

#include <stdio.h>
#include <stdlib.h>

#define ElementType int
typedef struct Node NodeType;
struct Node {
    ElementType index;
    int father;    // 是否为父结点
};
NodeType Error = {-1, 0};

#define MaxSize 30
typedef struct SNode *Stack;
struct SNode {
    NodeType Data[MaxSize];
    int Top;
}stack;

void makeEmpty()
{
    stack.Top = -1;
}

void Push(NodeType item)
{
    if (stack.Top == MaxSize - 1) return;
    else stack.Data[++(stack.Top)] = item;
}

NodeType Pop()
{
    if (stack.Top == -1) return Error;
    else return (stack.Data[(stack.Top)--]);
}

NodeType getTopItem()
{
    if (stack.Top == -1) return Error;
    else return (stack.Data[(stack.Top)]);
}

void printPostorder(int N)
{
    int i, flag;
    char preStr[5] = {'\0'}, str[5] = {'\0'};
    NodeType preNode, node, tmp;

    makeEmpty();

    flag = 0;
    scanf("%s %d", preStr, &preNode.index);
    for (i = 1; i < 2 * N; ++i) {
        scanf("%s", str);
        if (str[1] == 'u')
            scanf("%d", &node.index);
        if (preStr[1] == 'u') {   // 只要前一次是push就可直接压栈
            preNode.father = 0;
            Push(preNode);
        }
        else {  // 前一次为pop时
            if (str[1] == 'o') {    // 第二次也为pop时可以安全出栈并输出
                tmp = Pop();
                if (flag) printf(" ");
                printf("%d", tmp.index);
                flag = 1;
                // 如果此时栈顶元素是父节点，则依次输出所有栈顶的父节点
                tmp = getTopItem();
                while (tmp.father) {
                    Pop();
                    if (flag) printf(" ");
                    printf("%d", tmp.index);
                    tmp = getTopItem();
                }
            }
            else {  // 第二次为push时，说明此时的栈顶元素是有右孩子的父节点，需要pop出来修改其father字段再push回栈中
                tmp = Pop();
                tmp.father = 1;
                Push(tmp);
            }
        }
        preStr[1] = str[1]; // 由于每次只根据第二个字符判断是push还是pop，所以只更改第二个字符即可
        preNode = node;
    }
    // 输出栈中所有剩余结点
    tmp = Pop();
    while (tmp.index > 0) {
        if (flag) printf(" ");
        printf("%d", tmp.index);
        tmp = Pop();
    }
}

int main()
{
    int N;
    scanf("%d", &N);

    printPostorder(N);

    return 0;
}