Android 坐标系与视图坐标系图解

1.Android坐标系

在Android中，将屏幕的最左上角顶点作为Android坐标系的原点

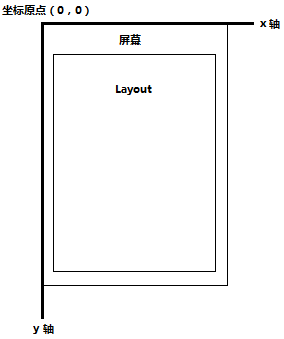
从原点向右是X轴的正方向，从原点向下是Y轴的正方向

View提供了getLocationOnScreen( int[] location)方法来获取在整个屏幕内的绝对坐标，该坐标值为View左上角的坐标。注意该View的坐标值是从屏幕左上角开始获取的，所以也包括了通知栏的高度
该方法的具体实现

    /**
     * <p>Computes the coordinates of this view on the screen. The argument
     * must be an array of two integers. After the method returns, the array
     * contains the x and y location in that order.</p>
     *
     * @param location an array of two integers in which to hold the coordinates
     */
    public void getLocationOnScreen(@Size(2) int[] location) {
        getLocationInWindow(location);

        final AttachInfo info = mAttachInfo;
        if (info != null) {
            location[0] += info.mWindowLeft;
            location[1] += info.mWindowTop;
        }
    }

可看到，传入的int[]数组中，location[0]代表的是X轴坐标，location[1]代表的Y轴坐标
这里还有个getLocationInWindow方法，作用是获取View在当前窗口内的绝对坐标
我们在通过MotionEvent类中的getRawX()，getRawY()方法获取的坐标同样也属于这种Android坐标系里的坐标

2.视图坐标系

Android中的视图坐标系，描述的是子视图与其父视图中的位置关系
和Android坐标系一样，视图坐标系也是以原点向右为X轴正方向，以原点向下为Y轴正方向，与Android坐标系不同的是，视图坐标系的原点是以父视图左上角的位置为原点

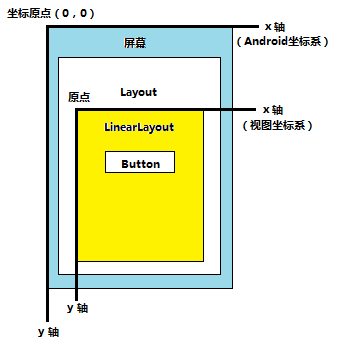
如上图中，对于Button来说，父视图LinearLayout左上角就是视图坐标系的原点(0,0)
我们通过MotionEvent类中的getX()、getY()方法所获得的就是视图坐标系的坐标

在Android中，系统提供了很多获取坐标值、相对距离等方法

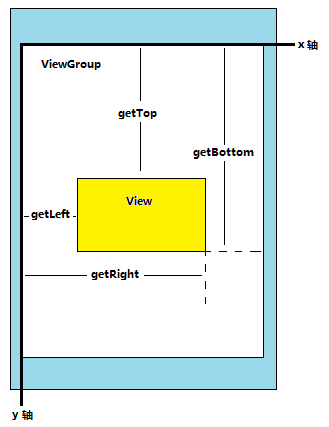
View提供的API

• getTop()：获取View顶边到其父布局顶边的距离
• getLeft()：获取View左边到其父布局左边的距离
• getRight()：获取View右边到其父布局左边的距离
• getBottom()：获取View底边到其父布局顶边的距离

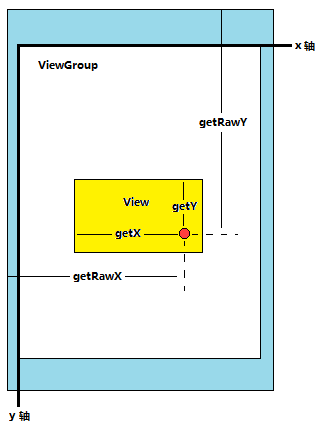
MotionEvent提供的API

• getX()：获取点击位置离View左边的距离
• getY()：获取点击位置离View顶边的距离
• getRawX()：获取点击位置离屏幕左边的距离
• getRawY()：获取点击位置离屏幕顶边的距离