【难】三者最小公倍数问题

暑假里乐乐报名参加了游泳、绘画和跆拳道等三个兴趣班，其中游泳班每隔2天上一次课，绘画班每隔3天上一次课，跆拳道每隔6天上一次课。已知7月1日乐乐在这三个兴趣班都上了课，则他在7、8两个月中不用上这三个兴趣班的天数是（）天。

A 25

B 26

C 28

D 27【正确答案】

解析

每隔2天上一次游泳班相当于每3天上一次，每隔3天上一次绘画班相当于每4天上一次，每隔6天上一次跆拳道课相当于每7天上一次。7、8月一共是31+31=62天，去掉7月1日三个班都上了，剩下61天。在剩下的61天中：上游泳班的天数有61÷3=20……1，即20天；上绘画班的次数有61÷4=15……1，即15天；上跆拳道班的有61÷7=8……5，即8天。同时上游泳班和绘画班的周期为3和4的最小公倍数12，则有61÷12=5……1，即5天；同时上绘画班和跆拳道的周期为4和7的最小公倍数28，则有61÷28=2……5，即2天；同时上游泳班和跆拳道的周期为3和7的最小公倍数21，则有61÷21=2……19，即2天。同时上三种培训班的周期为3，4，7的最小公倍数84，61天里不会出现。则7、8两个月不用上兴趣班的天数为61-（20+15+8-5-2-2）=61-34=27天。故正确答案为D。

这种题还是很难的，而且坑很多，每隔n天来一次等同于每n+1天来一次。还要知道七八月总共62天。答案4个选项都接近也增加了猜的难度。

这种题不建议穷举法，因为62还是蛮多的，全列出来比较耗时间，一般30以下的数量可以穷举。所以要么走算法，要么不做。

首先3、4、7的最小公倍数=84>62，因此不再存在3个课同一天上的情况，也就是说从7月2号开始的61天内，每天只有上0节、1节、2节的情况。现在要求0节的总天数。这不就是经典的三者容斥问题吗？但是不含中间三者共同重合部分。

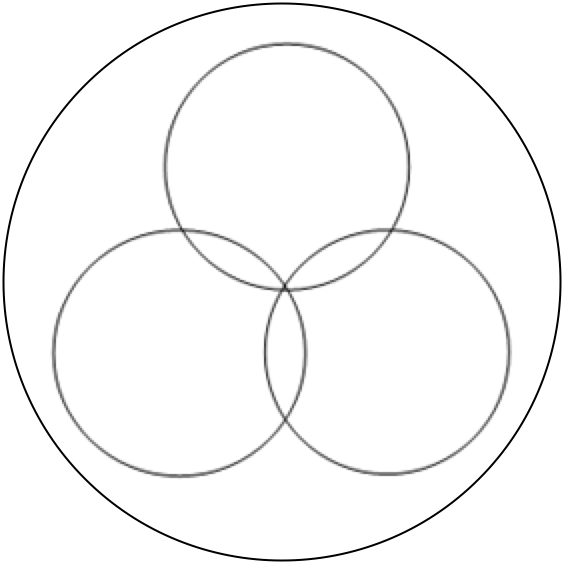
用总天数61分别减去三种课各自占据的天数，再分别加上每2种课公共的部分，其中天数要用61除之，向下取整。这里面计算量还挺大的，要多加练习。