题目描述:
Given n, how many structurally unique BST’s (binary search trees) that store values 1…n?
For example,
Given n = 3, there are a total of 5 unique BST’s.
动态规划来解决这道题:
我设bsTreeNum[i]表示共有i个节点时,能产生的BST树的个数
n == 0 时,空树的个数必然为1,因此bsTreeNum[0] = 1
n == 1 时,只有1这个根节点,数量也为1,因此bsTreeNum[1] = 1
n == 2时,
bsTreeNum[2] = bsTreeNum[0] * bsTreeNum[1] +bsTreeNum[1] * bsTreeNum[0]
n == 3时,
bsTreeNum[3] = bsTreeNum[0] * bsTreeNum[2] + bsTreeNum[1] * bsTreeNum[1] +bsTreeNum[2] * bsTreeNum[0]
同时,当根节点元素为 1, 2, 3, 4, 5, …, i, …, n时,基于以下原则的BST树具有唯一性:
以i为根节点时,其左子树构成为[0,…,i-1],其右子树构成为[i+1,…,n]构成
因此,dp[i] = sigma(dp[0…k] * dp[k+1…i]) 0 <= k < i - 1
我们得到了递推关系式,这是解决DP问题的关键!!!!
package suda.alex.leetcode;
import java.util.Scanner;
public class UniqueBSTree {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scanner = new Scanner(System.in);
System.out.println("input n:");
int n = scanner.nextInt();
System.out.println("the number of BST is:" + numTrees(n));
}
public static int numTrees(int n) {
if(n == 0){
return 1;
}
int[] bsTreeNum = new int[n+1];
bsTreeNum[0] = 1;
bsTreeNum[1] = 1;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
bsTreeNum[i] += bsTreeNum[j]*bsTreeNum[i-j-1];
}
}
return bsTreeNum[n];
}
}








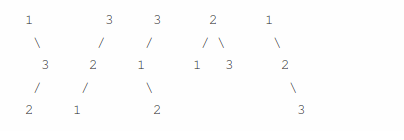














 92
92

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








