【LeetCode】5. Longest Palindromic Substring

最新推荐文章于 2024-10-11 23:48:39 发布

zjwreal

最新推荐文章于 2024-10-11 23:48:39 发布

阅读量1.5k

点赞数 1

分类专栏： LeetCode 文章标签： DP

本文链接：https://blog.csdn.net/zjwreal/article/details/80933232

版权

LeetCode 专栏收录该内容

297 篇文章 3 订阅

订阅专栏

5. Longest Palindromic Substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: "babad"

Output: "bab"

Note: "aba" is also a valid answer.

Example:

Input: "cbbd"

Output: "bb"

思路

最长回文子串。就是给定一个字符串S，找出其中的最长回文子串，并返回该子串。

解法1：暴力枚举时间复杂度 $O(n^3)$

解法2：中心扩展法时间复杂度 $O(n^2)$ 空间复杂度 $O(1)$

解法3：动态规划时间复杂度 $O(n^2)$ 空间复杂度 $O(n^2)$

解法4：Manacher算法时间复杂度 $O(N)$ 空间复杂度 $O(n)$

解法1：暴力枚举

遍历该字符串的每一个子串，判断是不是回文串，最后给出最长回文子串。

时间复杂度 $O(n^3)$ ，运行超时

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.size();
        if(len <= 1) return s;
        int maxlen = 0;
        string max_sub_string = "";
        for(int i = 0;i<len;i++){
            for(int j = i ; j < len ;j++){
                string sub_string = s.substr(i,j-i+1);
                if(isPalindrome(sub_string)){
                    if(sub_string.size()>maxlen){
                        maxlen = sub_string.size();
                        max_sub_string = sub_string;
                    }
                }
            }
        }
        return max_sub_string;
    }
    bool isPalindrome(string s){
        int slen = s.size();
        for(int i = 0;i<(slen+1)/2;i++){
            if(s[i]!=s[slen-1-i])
                return false;
        }
        return true;
    }
};

解法2：中心扩展法

优化：枚举回文串的中点

从某一个字符开始，左右向外扩展得到一个更长的子串，看是否是回文子串，如果是回文子串，则继续向外遍历，知道遇到非回文子串或者超出子串范围。需要注意针对一个字符向外扩张时，需要同时偶数字符个数回文子串和奇数字符个数回文子串两种情况。

时间复杂度 $O(n^2)$

空间复杂度 $O(1)$

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.size();
        if(len <= 1) return s;
        int maxlen = 0, left = 0,right = 0,substr_left,substr_right,substr_len;
        string max_sub_string = "";
        for(int i = 1;i<len;++i){
            left = i -1 ;
            right = i;
            // even Palindrome  eg. "abba"
            while(left >=0 && right < len && s[left]==s[right]){
                --left;
                ++right;
            }
            substr_left = left +1;
            substr_right = right -1;
            substr_len = substr_right -substr_left +1 ;
            if(substr_len > maxlen){
                max_sub_string = s.substr(substr_left,substr_len);
                maxlen = substr_len;
            }

            // odd Palindrome eg. "abcba"
            left = i-1;
            right = i+1;
            while(left >=0 && right < len && s[left]==s[right]){
                --left;
                ++right;
            }
            substr_left = left +1;
            substr_right = right -1;
            substr_len = substr_right -substr_left +1 ;
            if(substr_len > maxlen){
                max_sub_string = s.substr(substr_left,substr_len);
                maxlen = substr_len;
            }   
        }
        return max_sub_string;
    }
};

解法3：动态规划

时间复杂度 $O(n^2)$

空间复杂度 $O(n^2)$

首先写出动态转移方程：P[ i, j ] ← ( P[ i+1, j-1 ] and Si = Sj ) 显然，如果一个子串是回文串，并且如果从它的左右两侧分别向外扩展的一位也相等，那么这个子串就可以从左右两侧分别向外扩展一位。

其中的base case是

P[ i, i ] ← true
P[ i, i+1 ] ← ( Si = Si+1 )

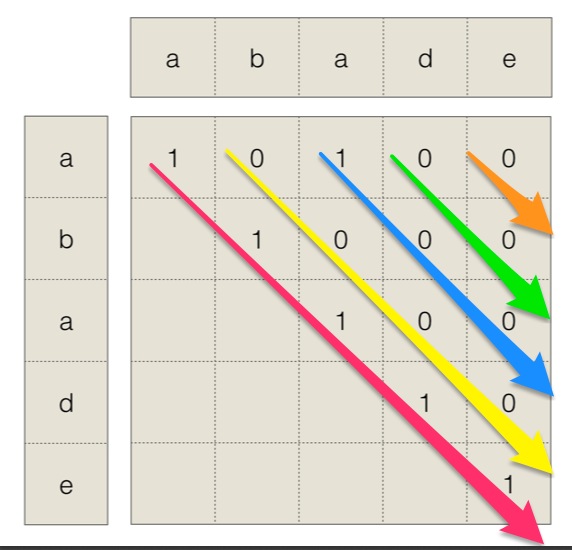
假设有个字符串是adade，现在要找到其中的最长回文子串。使用上面的动态转移方程，有如下的过程:

按照红箭头->黄箭头->蓝箭头->绿箭头->橙箭头的顺序依次填入矩阵，通过这个矩阵记录从i到j是否是一个回文串。

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.size();
        if(len <= 1) return s;
        int maxlen = 1 ,begin;
        bool dp[len][len]; // dp[i][j] == true -> s[i..j] is palindrome
        memset(dp,0,sizeof(dp));
        for(int i = 0; i<len ;i++){
            dp[i][i] = true; 
        }
        for(int i =0 ; i< len -1;i++){
            if(s[i]==s[i+1]){
                dp[i][i+1] = true;
                maxlen = 2;
                begin = i;
            }
        }
        for(int substr_len = 3; substr_len <= len ;substr_len ++){
            for(int i =0; i <= len -substr_len; i++){
                int j = i + substr_len -1 ;
                if(s[i] == s[j] && dp[i+1][j-1] == true){ 
                    dp[i][j] = true ;
                    begin = i;
                    maxlen = substr_len;
                }
            }
        }
        return s.substr(begin,maxlen);
    }
};

解法4：Manacher算法

时间复杂度 $O(n)$

空间复杂度 $O(n)$

Manacher算法

该算法首先对字符串进行预处理，在字符串的每个字符前后都加入一个特殊符号，比如字符串 abcd 处理成 #a#b#c#d#,为了避免处理越界，在字符串首尾加上不同的两个特殊字符(c类型的字符串尾部不用加，因为自带‘\0’)，这样预处理后最终变成$#a#b#c#d#^，经过这样处理后有个好处是原来的偶数长度和奇数长度的回文在处理后的字符串中都是奇数长度。假设处理后的字符串为s。

对于已经预处理好的字符串我们用数组p[i]来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]）,以字符串“12212321”为例，p数组如下

s：   $   #  1  #  2  #  2  #  1  #  2  #  3  #  2  #  1  #  ^ 
p：       1  2  1  2   5  2  1  4  1   2  1  6  1   2  1  2  1

可以看出，P[i]-1正好是原字符串中回文串的总长度, 如果p数组已知，遍历p数组找到最大的p[i]就可以求出最长回文的长度，也可以求出回文的位置

下面给出求p[]数组的方法：

设id是当前求得的最长回文子串中心的位置，mx为当前最长回文子串的右边界（回文子串不包括该右边界），即mx = id + p[id]。记j = 2*id – i ，即 j 是 i 关于 id 的对称点。

1、当i < mx 时，如下图。此时可以得出一个非常神奇的结论p[i] >= min(p[2*id - i], mx - i)，下面我们来解释这个结论

如何根据p[j]来求p[i]呢，又要分成两种情况

（1.1）当mx – i > p[j], 这时候以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以 P[i] 至少等于 p[j], 后面的再继续匹配。如下图

*注：这里其实p[i]一定等于p[j],后面不用再匹配了。因为如果p[i]后面还可以继续匹配，根据对称性，p[j]也可以继续扩展了*

（1.2）当mx – i <= p[j]，以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] 至少等于 mx - i，至于mx之后的部分是否对称，就只能老老实实去匹配了。

注：如果mx – i < p[j] ，这时p[i]一定等于mx - i, 因为如果p[i]在mx之后还可以继续匹配，根据对称性，mx之后匹配的点(包括mx)一定会出现在my的前面，这说明p[id]也可以继续扩展了

class Solution {
public:
    string longestPalindrome(string s) {
        if(s.size() <= 1) return s;
        int id=0,mx=0;
        // Manacher Algorithm
        string str = preProcess(s);
        int len = str.size();
        vector<int> p(len,0);
        for(int i =1; i< len-1;i++){
            p[i] = mx > i ? min(p[2*id -i],mx-i):1; //mx为当前最长回文子串的右边界
            while(str[i+p[i]] == str[i-p[i]]) // 计算P[i] 
                p[i]++;
            if( i + p[i] > mx){
                mx = i+ p[i];
                id = i;
            }
        }
        // 遍历p，寻找最大回文长度 
        int maxlen =0,index =0;
        for(int i =1;i<len-1;i++){
            if(p[i] > maxlen){
                maxlen = p[i];
                index = i;
            }
        }
        return s.substr((index - maxlen)/2,maxlen-1);   //p[i]-1为原字符串中的回文子串长度 
    }
    string preProcess(string &s){
        int n = s.size();
        string res;
        res.push_back('$');
        res.push_back('#');
        for(int i = 0; i<n ;i++){
            res.push_back(s[i]);
            res.push_back('#');
        }
        res.push_back('^');
        return res;
    }
};