题目：struc2vec: Learning Node Representations from Structural Identity
作者：Leonardo F. R. Ribeiro, Pedro H. P. Saverese, Daniel R. Figueiredo
来源：KDD 2017
传统的graph embedding方法如DeepWalk，LINE，SDNE等都是基于近邻相似假设的（Homohily，同质性），两个顶点的共同邻居越多则越相似。然而在一些场景中，两个不是近邻的顶点也可能拥有很高的相似性，可能这些节点在邻域中的角色相似，例如星型结构的中心节点，社区结构之间的桥接节点等。struc2vec就是针对捕捉节点的结构化角色相似度（structural role proximity）提出的模型。
模型
struc2vec总体流程如下：
（1）根据不同距离的邻居信息，分别计算计算节点对的结构相似度 f k ( u , v ) f_k(u,v) fk(u,v) （第k层u和v节点的结构相似度）
（2）构造多层带权有向图 M，其中每层都是带权无向图，层与层之间是有向的
（3）在M中随机游走，构造上下文序列
（4）skip-gram训练序列，得到每个节点的表示
相似度定义
struc2vec从空间结构相似性的角度定义顶点相似度。下图中如果在基于近邻相似的模型中，顶点u和顶点v是不相似的，第一他们不直接相连，第二他们不共享任何邻居顶点。
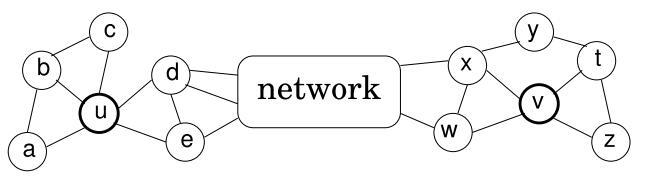
但是在struc2vec的假设中，顶点u和顶点v是具有空间结构相似的。他们的度数分别为5和4，分别连接3个和2个三角形结构，通过2个顶点(d,e;x,w)和网络的其他部分相连。
直观来看，如果两个顶点的度相同，那么这两个顶点的结构是相似的，若各自邻接顶点仍然具有相同度数，那么他们的相似度就更高。
顶点对距离定义
令 表示到顶点u距离为k的顶点集合，则
表示是u的直接相连近邻集合。
令 表示顶点集合S的有序度序列。
通过比较两个顶点之间距离为k的环路上的有序度序列可以推出一种层次化衡量结构相似度的方法。
令 表示顶点u和v之间距离为k（这里的距离k实际上是指距离小于等于k的节点集合）的环路上的结构距离(注意是距离，不是相似度)。
其中 是衡量有序度序列
和
的距离的函数，并且
。
注意到的计算是在
上加上一个非负的值，因此该函数关于k是一个单调不降的函数。并且这个函数只有在两个节点同时存在k跳邻域的时候才有定义。
下面给出一个具体例子：
下面就是如何定义有序度序列之间的比较函数了，由于 和
的长度不同，并且可能含有重复元素。所以文章采用了**Dynamic Time Warping(DTW)**来衡量两个有序度序列。
一句话，DTW可以用来衡量两个不同长度且含有重复元素的的序列的距离（距离的定义可以自己设置）。
基于DTW，定义元素之间的距离函数
至于为什么使用这样的距离函数，这个距离函数实际上惩罚了当两个顶点的度数都比较小的时候两者的差异。举例来说， 情况下的距离为1，
情况下的距离差异为0.0099。这个特性正是我们想要的。
构建层次带权图
根据上一节的距离定义，对于每一个 我们都可以计算出两个顶点之间的一个距离，现在要做的是通过上一节得到的顶点之间的有序度序列距离来构建一个层次化的带权图（用于后续的随机游走）。
每一层是一个带权完全图（任意两个节点都有边相连），因此有 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1) 条边
我们定义在某一层k中两个顶点的边权为
这样定义的边权都是小于1的，当且仅当距离为0的是时候，边权为1。
通过有向边将属于不同层次的同一顶点连接起来，具体来说，对每个顶点，都会和其对应的上层顶点还有下层顶点相连。边权定义为
其中 是第k层与u相连的边的边权大于平均边权的边的数量。
，
就是第k层所有边权的平均值。
第k层所有边权的平均值。
实际上表示了第k层中，有多少节点是与节点u相似的，如果u与很多节点都相似，说明此时一定处于低层次，考虑的信息太少，那么
将会很大，即
，对于这种情况，就不太适合将本层中的节点作为上下文了，应该考虑跳到更高层去找合适的上下文，所以高层的权重更大。
采样获取顶点序列
使用有偏随机游走在构造出的图 中进行顶点序列采样。 每次采样时，首先决定是在当前层游走，还是切换到上下层的层游走。
具体的，假设随机游走走到了，那么它下一步可能的走向是
（见上图左半边）。留在本层继续游走的概率为q，自然跳层的概率就是1-q。
若决定在当前层游走，设当前处于第k层，则从顶点u到顶点v的概率为：
(6)
p
k
(
u
,
v
)
=
e
−
f
k
(
u
,
v
)
Z
k
(
u
)
p_{k}(u, v)=\frac{e^{-f_{k}(u, v)}}{Z_{k}(u)}\tag{6}
pk(u,v)=Zk(u)e−fk(u,v)(6)
其中分母
(7)
Z
k
(
u
)
=
∑
v
∈
V
v
≠
u
e
−
f
k
(
u
,
v
)
Z_{k}(u)=\sum_{v \in V \atop v \neq u} e^{-f_{k}(u, v)}\tag{7}
Zk(u)=v̸=uv∈V∑e−fk(u,v)(7)
是第k层中关于顶点u的归一化因子。
通过在图M中进行随机游走，每次采样的顶点更倾向于选择与当前顶点结构相似的顶点。因此，采样生成的上下文顶点很可能是结构相似的顶点，这与顶点在图中的位置无关。
若决定切换不同的层，则以如下的概率选择 层或
层，
(8)
p
k
(
u
k
,
u
k
+
1
)
=
w
(
u
k
,
u
k
+
1
)
w
(
u
k
,
u
k
+
1
)
+
w
(
u
k
,
u
k
−
1
)
p
k
(
u
k
,
u
k
−
1
)
=
1
−
p
k
(
u
k
,
u
k
+
1
)
\begin{aligned} p_{k}\left(u_{k}, u_{k+1}\right) &=\frac{w\left(u_{k}, u_{k+1}\right)}{w\left(u_{k}, u_{k+1}\right)+w\left(u_{k}, u_{k-1}\right)} \\ p_{k}\left(u_{k}, u_{k-1}\right) &=1-p_{k}\left(u_{k}, u_{k+1}\right) \end{aligned}{\tag 8}
pk(uk,uk+1)pk(uk,uk−1)=w(uk,uk+1)+w(uk,uk−1)w(uk,uk+1)=1−pk(uk,uk+1)(8)
注意到当层数越高，因为考虑的邻域更广，节点间的结构相似性计算越苛刻，因此在底层计算出两个节点结构相似的，在高层则不一定相似，并且高层很多节点之间的可能根本没有定义。这就导致如果随机游走在某个节点u跳到了更高的层，那么在随机游走的序列中，其左边的节点是k层，而右边的节点是k+1层的。而左右两边的取值范围是不同的。换言之，某个节点可能会出现在左边，但不会出现在右边，因为虽然它跟中间那个节点u在k层是相似的，但在k+1层可能无定义或者
太大导致随机游走在k=1层走到这个节点的概率几乎可以忽略。
另外从源码可以发现，当在节点u处跳层时，只会添加一次节点，而不会将
都添加到随机游走中。
优化
了解了算法的流程后，逐步分析算法的复杂性
DTW计算序列距离： ，通过一定的优化可以降到
，
l
l
l是序列的最大长度。
度序列的长度：
第k层一共要计算 个节点对，第k层的复杂度：
总共k层：
这个复杂度太高了，为此作者提供了3种优化算法：
OPT1 有序度序列长度优化
前面提到过对于每个顶点在每一层都有一个有序度序列，而每一个度序列的空间复杂度为O(n)。
文章提出一种压缩表示方法，对于序列中出现的每一个度，计算该度在序列里出现的次数。压缩后的有序度序列存储的是**(度数，出现次数)**这样的二元组。比如{1,1,1,1,2,2,5,5,5,8}压缩成{(1,4),(2,2),(5,3),(8,1)}。
同时修改距离函数为：
为度数，
为度的出现次数。
OPT2 相似度计算优化
在原始的方法中，我们需要计算每一层k中，任意两个顶点之间的相似度。事实上，这是不必要的。因为两个度数相差很大的顶点，即使在 的时候他们的距离也已经非常大了，那么在随机游走时这样的边就几乎不可能被采样到，所以我们也没必要计算这两个顶点之间的距离。
文章给出的方法是在计算顶点u和其他顶点之间的距离时，只计算那些与顶点u的度数接近的顶点的距离。具体来说，在顶点u对应的有序度序列中进行二分查找，查找的过程就是不断逼近顶点u的度数的过程，只计算查找路径上的顶点与u的距离。 这样每一次需要计算的边的数量从 数量级缩减到
。
OPT3 限制层次带权图层数
层次带权图M中的层数是由图的直径 决定的。但是对很多图来说，图的直径会远远大于顶点之间的平均距离。
当k接近 时，环上的度序列
长度也会变得很短，
和
会变得接近。
因此将图中的层数限制为 ，使用最重要的一些层来评估结构相似度。
这样的限制显著降低构造M时的计算和存储开销。
4247
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
