假定:裁剪窗口为矩形窗口,左下点坐标为(xl, yb), 右上点坐标为(xr, yt)。
直线段的裁剪
直线段与窗口的位置关系有以下几种情况:
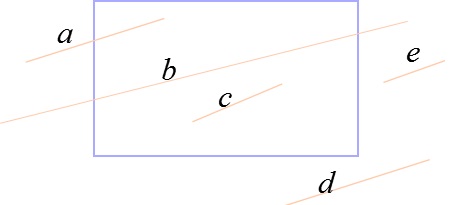
⑵ 直线段两个端点在窗口外,且与窗口不相交(线段d和e);
⑷ 直线段一个端点在窗口内,一个端点在窗口外(线段a)。
编码裁剪算法(也称Cohen-Sutherland算法)
该算法基于以下考虑:每一线段或者整个位于窗口内部,或者被窗口分割而使其中的一部分舍弃。
算法步骤:
第1步:确定一条线段是否整个位于窗口内,若是,则取之;
第2步:确定该线段是否整个位于窗口外,若是,则弃之;
第3步:若第1、2步判断均不成立,则通过窗口边界所在的直线将线段分成两部分,再对每一部分进行第1、2步的测式。
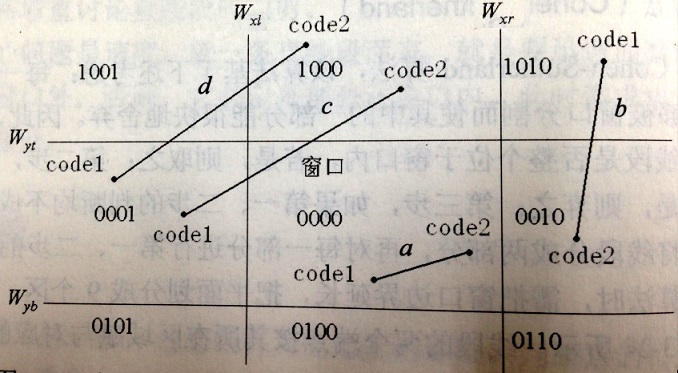
区域编码:
实现该算法时,需延长窗口边界,把平面划分为9个区域,每个区域用4位二进制代码表示。线段的两个端点按其所在区域赋与对应的代码,4位代码的意义如下(从右到左):
编码规则可知:
①若两个端点编码都为0000,则直线段全部位于窗口内;
②若两个端点编码的位逻辑乘(按位与)不为0,则整条线段位于窗口外;
③若线段不能由以上两种测试决定,则可能部分可见,需求交点,把线段再分割。
分割方法:
计算出直线段与窗口某一边界(或边界延长线)的交点,再用上述①、 ②两种条件判别分割后的两条线段,舍弃位于窗口外的一段。
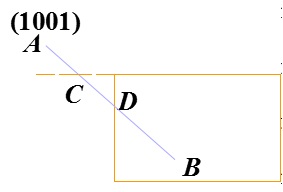
例:用编码裁剪算法对AB线段裁剪,可以在C点分割,对AC、CB进行判别,舍弃AC,再分割于D点,对CD、DB作判别,舍弃CD,而DB全部位于窗口内,算法结束。
线段编码不同分布情况下裁剪线段可见性分析:
①线段a全部在窗口内,则全部显示,不需要求交点;
②线段b全部在窗口外(在窗口同侧),则全部不显示,不需要求交点;
③线段c一部分在窗口内,一部分在窗口外,则需要先求交点,再显示两交点之间的线段;
④线段d全部在窗口外(跨越三个区域),则只需要求交点一次即可判定剩下的线段全部在窗口外。
关于算法实现过程中的几点说明:
1)一般按固定顺序检测区号的各位是否为0。可按左→右→下→上或上→下→右→左的顺序。
2)欲舍弃窗口外的子线段,只要用交点的坐标值取代被舍弃端点的坐标即可。
3)当需要求交点时,不必把线段与每条窗口边界都求交,只要按顺序检测到端点区码的某位不为0时,才把线段与对应的窗口边界求交。
编码裁剪算法的特点:
编码方法直观方便,速度较快,是一种较好的裁剪方法,但有两个问题有待进一步解决:
①采用位逻辑乘(按位与)的运算,在有些高级语言中不便进行;
②全部舍弃的判断只适合于那些仅在窗口同侧的线段(如线段b),对于跨越三个区域的线段(如线段d),则不能一次作出判别而舍弃它们。
中点分割裁剪算法
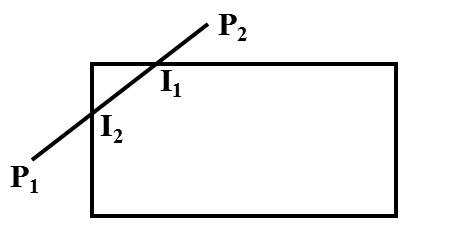
基本思想:分别寻找直线段两个端点各自对应的最远可见点,这两个最远可见点之间的线段即为要输出的可见段。
线段P1、P2的端点P1的最远可见点为I1,端点P2的最远可见点为I2,则线段I1、I2为输出的可见部分。
中点分割裁剪算法的步骤:
以找出直线段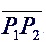
⑴ 判断直线段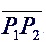
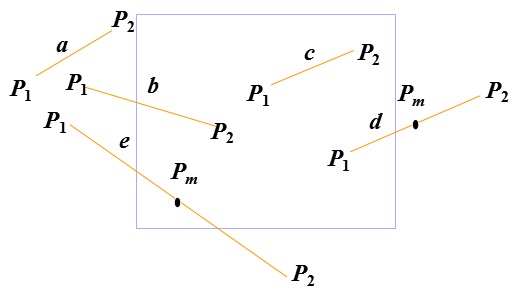
⑵ 判断P2点是否可见,若是,则P2点即为距P1点最远的可见点(图中b),返回;否则,继续⑶。
⑶ 将直线段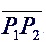
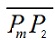
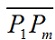
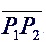
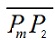
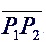
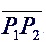
重复上述过程,直到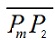
找到了距P1点的最远可见点后,把两个端点对调一下,即对直线段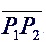
中点分割裁剪算法的特点:
该算法中求线段中点可以由加法和移位来实现(除2运算可用移位完成),避免使用了乘除法。因此,该算法易于用硬件来实现。如果允许两个找最远可见点的过程平行进行,则裁剪速度更快。
























 3120
3120

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








