1.一个实验
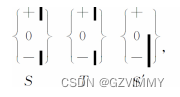
一束粒子穿S装置(包含两段等距相反的均匀磁场),因某种性质(自旋为1的粒子)会分成三束,挡住下面两束后穿过完全相同的装置结果如下:

结果记为:

旋转装置:

概率应满足归一性:

然后做下述实验:

测试结果:
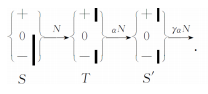

(T不放挡板时没有粒子通过,相当于没有用T改变基础态)

结论:

用i/j标识+/0/-等基础态,我们得到下面三个基本结论:


这里的A是任意的,其中可以加挡板/旋转角度/增加电场磁场。
一旦确认下来,在1的基础上(自旋为1),可以用9个数字的矩阵表示:

这就是我们后面大量提及的算符。
2.认识自旋
磁偶极矩:
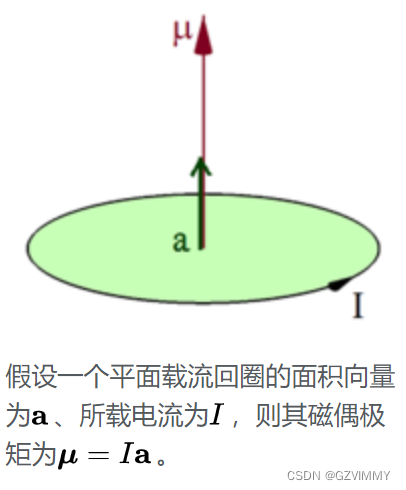
电子是带 (−1e) 的 带电粒子 ,单位为基本电荷,他的角动量来自两种方向,自旋和轨道方向。从经典电磁学中知,电荷会产生磁偶极矩,并产生磁极,而两端产生的磁极性机率是一样的。这个电子就有如一个磁铁一样。其中一个结果是当外加一个磁场时,而产生一个转矩,磁矩方向是依据场的方向。
如果电子被视为一个古典的带电粒子,透过转动可知角动量L,和磁偶极矩μ 得下式:

me代表的是电子的不变质量,请注意角动量L在此可以是自旋角动量,轨道角动量,或是总角动量。

用任何方法也无法测量电子的角动量和磁偶极矩,但是却可以测量沿着定轴的分量,如:

自旋为1/2的情况:

3.泡利算符

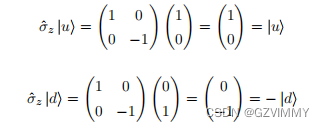
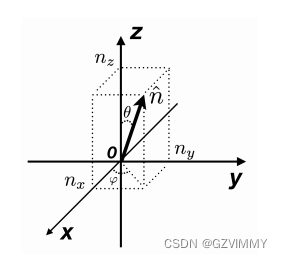

操作流程如下:

Y轴的情况自行推导,这个给出最后的结论:

有了这个我们就可以计算任意的角度概率了


归纳起来就是:

因为它有个很巧妙的应用:









 本文探讨量子力学中的算符概念,通过实验解释电子自旋现象,展示磁偶极矩和角动量的关系,并介绍了自旋为1/2的特殊情况。此外,还提及了泡利算符在计算不同角度概率中的应用。
本文探讨量子力学中的算符概念,通过实验解释电子自旋现象,展示磁偶极矩和角动量的关系,并介绍了自旋为1/2的特殊情况。此外,还提及了泡利算符在计算不同角度概率中的应用。

















 582
582

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








