Kmeans（K均值）与Kmeans++和KNN（K近邻）算法比较

最新推荐文章于 2023-04-20 14:37:12 发布

zll0927

最新推荐文章于 2023-04-20 14:37:12 发布

阅读量1.5w

点赞数 17

本文链接：https://blog.csdn.net/zll0927/article/details/17000675

版权

K-Means介绍

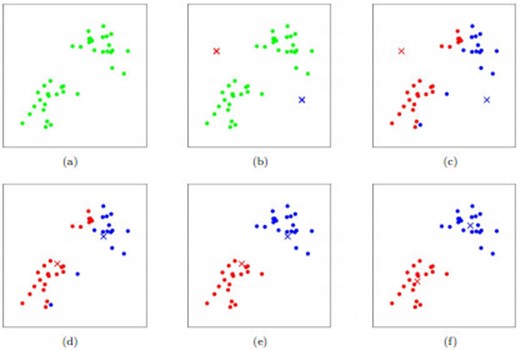
K-means算法是聚类分析中使用最广泛的算法之一。它把n个对象根据他们的属性分为k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。其聚类过程可以用下图表示：

如图所示，数据样本用圆点表示，每个簇的中心点用叉叉表示。(a)刚开始时是原始数据，杂乱无章，没有label，看起来都一样，都是绿色的。(b)假设数据集可以分为两类，令K=2，随机在坐标上选两个点，作为两个类的中心点。(c-f)演示了聚类的两种迭代。先划分，把每个数据样本划分到最近的中心点那一簇；划分完后，更新每个簇的中心，即把该簇的所有数据点的坐标加起来去平均值。这样不断进行”划分—更新—划分—更新”，直到每个簇的中心不在移动为止。

该算法过程比较简单，但有些东西我们还是需要关注一下，此处，我想说一下"求点中心的算法"

一般来说，求点群中心点的算法你可以很简的使用各个点的X/Y坐标的平均值。也可以用另三个求中心点的的公式：

1）Minkowski Distance 公式 —— λ 可以随意取值，可以是负数，也可以是正数，或是无穷大。

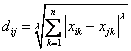
2）Euclidean Distance 公式 —— 也就是第一个公式 λ=2 的情况

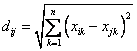
3）CityBlock Distance 公式 —— 也就是第一个公式 λ=1 的情况

这三个公式的求中心点有一些不一样的地方，我们看下图（对于第一个 λ 在 0-1之间）。

（1）Minkowski Distance （2）Euclidean Distance （3）CityBlock Distance

上面这几个图的大意是他们是怎么个逼近中心的，第一个图以星形的方式，第二个图以同心圆的方式，第三个图以菱形的方式。

Kmeans算法的缺陷

聚类中心的个数K 需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适
Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。（可以使用Kmeans++算法来解决）

针对上述第2个缺陷，可以使用Kmeans++算法来解决

K-Means ++ 算法

k-means++算法选择初始seeds的基本思想就是：初始的聚类中心之间的相互距离要尽可能的远。

从输入的数据点集合中随机选择一个点作为第一个聚类中心
对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
重复2和3直到k个聚类中心被选出来
利用这k个初始的聚类中心来运行标准的k-means算法

从上面的算法描述上可以看到，算法的关键是第3步，如何将D(x)反映到点被选择的概率上，一种算法如下：

先从我们的数据库随机挑个随机点当“种子点”
对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。
重复2和3直到k个聚类中心被选出来
利用这k个初始的聚类中心来运行标准的k-means算法

可以看到算法的第三步选取新中心的方法，这样就能保证距离D(x)较大的点，会被选出来作为聚类中心了。至于为什么原因比较简单，如下图所示：

假设A、B、C、D的D(x)如上图所示，当算法取值Sum(D(x))*random时，该值会以较大的概率落入D(x)较大的区间内，所以对应的点会以较大的概率被选中作为新的聚类中心。

k-means++代码：http://rosettacode.org/wiki/K-means%2B%2B_clustering

KNN(K-Nearest Neighbor)介绍

算法思路：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。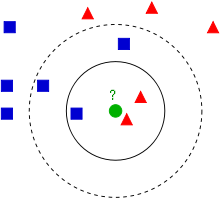

看下面这幅图：

KNN的算法过程是是这样的：

从上图中我们可以看到，图中的数据集是良好的数据，即都打好了label，一类是蓝色的正方形，一类是红色的三角形，那个绿色的圆形是我们待分类的数据。

如果K=3，那么离绿色点最近的有2个红色三角形和1个蓝色的正方形，这3个点投票，于是绿色的这个待分类点属于红色的三角形

如果K=5，那么离绿色点最近的有2个红色三角形和3个蓝色的正方形，这5个点投票，于是绿色的这个待分类点属于蓝色的正方形

我们可以看到，KNN本质是基于一种数据统计的方法！其实很多机器学习算法也是基于数据统计的。

KNN是一种memory-based learning，也叫instance-based learning，属于lazy learning。即它没有明显的前期训练过程，而是程序开始运行时，把数据集加载到内存后，不需要进行训练，就可以开始分类了。

具体是每次来一个未知的样本点，就在附近找K个最近的点进行投票。

再举一个例子，Locally weighted regression (LWR)也是一种 memory-based 方法，如下图所示的数据集。

用任何一条直线来模拟这个数据集都是不行的，因为这个数据集看起来不像是一条直线。但是每个局部范围内的数据点，可以认为在一条直线上。每次来了一个位置样本x，我们在X轴上以该数据样本为中心，左右各找几个点，把这几个样本点进行线性回归，算出一条局部的直线，然后把位置样本x代入这条直线，就算出了对应的y，完成了一次线性回归。也就是每次来一个数据点，都要训练一条局部直线，也即训练一次，就用一次。LWR和KNN很相似，都是为位置数据量身定制，在局部进行训练。

KNN和K-Means的区别

KNN	K-Means
1.KNN是分类算法 2.监督学习 3.喂给它的数据集是带label的数据，已经是完全正确的数据	1.K-Means是聚类算法 2.非监督学习 3.喂给它的数据集是无label的数据，是杂乱无章的，经过聚类后才变得有点顺序，先无序，后有序
没有明显的前期训练过程，属于memory-based learning	有明显的前期训练过程
K的含义：来了一个样本x，要给它分类，即求出它的y，就从数据集中，在x附近找离它最近的K个数据点，这K个数据点，类别c占的个数最多，就把x的label设为c	K的含义：K是人工固定好的数字，假设数据集合可以分为K个簇，由于是依靠人工定好，需要一点先验知识

相似点：都包含这样的过程，给定一个点，在数据集中找离它最近的点。即二者都用到了NN(Nears Neighbor)算法，一般用KD树来实现NN。