多元数组乘法的操作过程
1.点乘操作:各个矩阵对应元素做乘法
首先要搞清楚四个对应的概念
tf.matmul()为矩阵的乘法
tf.multiply()为矩阵的点乘
np.dot()为矩阵的乘法
np.multiply()为矩阵的点乘
import numpy as np
a = [[[0,1,2],[3,4,5]]]
np_a = np.array(a)
print(np_a.shape)
b = [[[6],[7]],[[8],[9]],[[10],[11]]]
np_b = np.array(b)
print(np_b.shape)
results1 = np_a*np_b
print(results1.shape)
results2 = np_b*np_a
print(results2.shape)
results3 = np.multiply(np_a,np_b)
print('results1 = ')
print(results1)
print('results2 = ')
print(results2)
print('results3 = ')
print(results3)
这里面的a.shape = (1,2,3),b.shape=(3,2,1),此时无论是
a
∗
b
a*b
a∗b还是
b
∗
a
b*a
b∗a,结果都为(3,2,3),也就是说点乘的结果与乘法的顺序无关,这里我们观察一下矩阵乘法的操作过程:
a
=
[
[
[
0
,
1
,
2
]
,
[
3
,
4
,
5
]
]
]
a = [[[0,1,2],[3,4,5]]]
a=[[[0,1,2],[3,4,5]]],
b
=
[
[
[
6
]
,
[
7
]
]
,
[
[
8
]
,
[
9
]
]
,
[
[
10
]
,
[
11
]
]
]
b = [[[6],[7]],[[8],[9]],[[10],[11]]]
b=[[[6],[7]],[[8],[9]],[[10],[11]]],此时
a
∗
b
的
结
果
为
a*b的结果为
a∗b的结果为
[
[
[
0
,
6
,
12
]
,
[
21
,
28
,
35
]
]
,
[
[
0
,
8
,
16
]
,
[
27
,
36
,
45
]
]
,
[
[
0
,
10
,
20
]
,
[
33
,
44
,
55
]
]
]
[[[0,6,12],[21,28,35]],[[0,8,16],[27,36,45]],[[0,10,20],[33,44,55]]]
[[[0,6,12],[21,28,35]],[[0,8,16],[27,36,45]],[[0,10,20],[33,44,55]]]
此时得到结果是分别使用矩阵进行相乘:
[
0
,
1
,
2
]
∗
[
6
]
=
[
0
,
6
,
12
]
[0,1,2]*[6] = [0,6,12]
[0,1,2]∗[6]=[0,6,12],
[
3
,
4
,
5
]
∗
[
7
]
=
[
21
,
28
,
35
]
[3,4,5]*[7] = [21,28,35]
[3,4,5]∗[7]=[21,28,35],…最终得到一个(3,2,3)的对应数组。
变换一下对应的维度,a.shape = (3,2,3),b.shape = (1,2,3),相乘之后仍然能够得到对应的结果:
import numpy as np
a = [[[0,1,2],[3,4,5]],[[0,1,2],[3,4,5]],[[0,1,2],[3,4,5]]]
np_a = np.array(a)
print(np_a.shape)
#b = [[[6,6],[7,7]],[[8,8],[9,9]],[[10,10],[11,11]]]
b = [[[0,1,2],[3,4,5]]]
np_b = np.array(b)
print(np_b.shape)
results1 = np_a*np_b
print(results1.shape)
results2 = np_b*np_a
print(results2.shape)
results3 = np.multiply(np_a,np_b)
print('results1 = ')
print(results1)
print('results2 = ')
print(results2)
print('results3 = ')
print(results3)
这里我们再次变换一下a的维度和b的维度,来查看最后结果的变化。
x = np.array([1])
y = np.array([[1,2],[3,4]])
results = x*y
print(results)
这里的x = (1,1),y = (2,2),此时两矩阵点乘的结果为(2,2)
当我们将a的维度变化为(2,2,3),b的维度变化为(6,2,1)的时候,矩阵相乘会相应的报错,此时的维度不符合题目要求。
总结一下点乘的规律:若w为
m
∗
1
m*1
m∗1的矩阵,x为
m
∗
n
m*n
m∗n的矩阵,那么通过点乘结果就会得到一个
m
∗
n
m*n
m∗n的矩阵
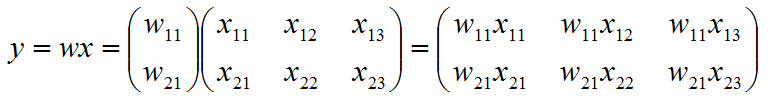 若w为
1
∗
n
1*n
1∗n的矩阵,x为
m
∗
n
m*n
m∗n的矩阵,那么通过点乘结果也会产生一个
m
∗
n
m*n
m∗n的矩阵
若w为
1
∗
n
1*n
1∗n的矩阵,x为
m
∗
n
m*n
m∗n的矩阵,那么通过点乘结果也会产生一个
m
∗
n
m*n
m∗n的矩阵
 若w为
m
∗
n
m*n
m∗n的矩阵,x为
m
∗
n
m*n
m∗n的矩阵,那么通过点乘结果就会得到一个
m
∗
n
m*n
m∗n的矩阵
若w为
m
∗
n
m*n
m∗n的矩阵,x为
m
∗
n
m*n
m∗n的矩阵,那么通过点乘结果就会得到一个
m
∗
n
m*n
m∗n的矩阵
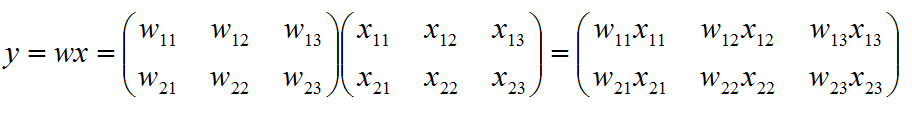 总而言之就是,点乘矩阵的最左的维度和最右的维度要么为1,要么相同,其他维度相乘的时候才能进行点乘,点乘的结果维度中间维度相同,最左最右的维度为两侧的最大维度
总而言之就是,点乘矩阵的最左的维度和最右的维度要么为1,要么相同,其他维度相乘的时候才能进行点乘,点乘的结果维度中间维度相同,最左最右的维度为两侧的最大维度
2.矩阵乘法操作:按照矩阵乘法的规则做运算
若w为
m
∗
p
m*p
m∗p的矩阵,x为
p
∗
n
p*n
p∗n的矩阵,那么通过矩阵相乘结果就会得到一个
m
∗
n
m*n
m∗n的矩阵,只有当w的列数==x的行数时,才能进行乘法运算:
 接下来我们来探讨多维矩阵的乘法,首先我们查看(1,2,3)矩阵与(1,3,2)矩阵相乘:
接下来我们来探讨多维矩阵的乘法,首先我们查看(1,2,3)矩阵与(1,3,2)矩阵相乘:
import numpy as np
x = np.array([[[1,2,3],[4,5,6]]])
y = np.array([[[1,2],[3,4],[5,6]]])
print(x.shape)
print(y.shape)
results = np.dot(x,y)
print(results)
这里出现的x.shape = (1,2,3),y.shape = (1,3,2),此时使用results = np.dot(x,y)之后乘积的结果为(1,2,1,2)。
对于多维矩阵的乘法,这里我们看对应的几个例子,就能够很好的理解多维矩阵乘法的操作:
1.如果a.shape = (1,2,3,4,5),b.shape = (5,4),则np.dot(a,b)的结果为(1,2,3,4,4)
2.如果a.shape = (1,2,3,4,5),b.shape = (6,5,4),则np.dot(a,b)的结果为(1,2,3,4,6,4)
这里的
(
1
,
2
,
3
,
4
,
5
)
∗
(
6
,
5
,
4
)
=
(
1
,
2
,
3
,
4
,
6
,
4
)
(1,2,3,4,5)*(6,5,4) = (1,2,3,4,6,4)
(1,2,3,4,5)∗(6,5,4)=(1,2,3,4,6,4),可以通过
(
1
,
2
,
3
,
4
,
5
)
∗
(
5
,
4
)
(1,2,3,4,5)*(5,4)
(1,2,3,4,5)∗(5,4)来理解
下面我使用一段图形化说明,来说明一下矩阵乘法的过程中维度的变化
这里设计a.shape = (1,2,3),b.shape = (4,3,2)
这里的
a
∗
b
=
(
1
,
2
,
3
)
∗
(
4
,
3
,
2
)
=
(
1
,
2
,
4
,
2
)
a*b = (1,2,3)*(4,3,2) = (1,2,4,2)
a∗b=(1,2,3)∗(4,3,2)=(1,2,4,2),
首先我们分析最后一列的列数是2,这里的列数对应着b的列数,对应的情况如下:
 这里对应的列数为2正好是b对应的列数,由此可以看出最后一个维度。注意上面一波数组全是由[0 1 2]乘以对应的矩阵乘出来的,对应的图片如下:
这里对应的列数为2正好是b对应的列数,由此可以看出最后一个维度。注意上面一波数组全是由[0 1 2]乘以对应的矩阵乘出来的,对应的图片如下:
 [0 1 2]乘以倒数第二维的结果
[0 1 2]乘以倒数第二维的结果
 [0 1 2]乘以最后一维的结果
[0 1 2]乘以最后一维的结果
 通过上面4个图片的显示可以看出,倒数第二个维度的对应坐标也是由[0 1 2]依次乘上对应的b维度的倒数第三维得到,(中间一个维度3在做乘法)
通过上面4个图片的显示可以看出,倒数第二个维度的对应坐标也是由[0 1 2]依次乘上对应的b维度的倒数第三维得到,(中间一个维度3在做乘法)
 两个矩阵相乘的过程之中消耗掉了,因为
[
0
,
1
,
2
]
[0,1,2]
[0,1,2]中的对应3列正好对应着
两个矩阵相乘的过程之中消耗掉了,因为
[
0
,
1
,
2
]
[0,1,2]
[0,1,2]中的对应3列正好对应着
[
18
,
19
]
[18,19]
[18,19]
[
20
,
21
]
[20,21]
[20,21]
[
22
,
23
]
[22,23]
[22,23]
中的3行,所以相乘之后三行乘以三列就消耗掉了,而由于对于b数组而言,最后两维度正好是b对应的两个维度,所以最后两个维度就是(4,2)。
同理,第二个矩阵的维度如果为(3,4,2)的情况下,倒数第三个维度会在(4,2)的基础上依次向前顺沿一个数值3,我们这里再看前面的数值维度是如何形成的。

 可以看出这里的第一个括号正好是相乘矩阵的第一个中括号,对应着第一个维度1
可以看出这里的第一个括号正好是相乘矩阵的第一个中括号,对应着第一个维度1
 第二个括号为之前相乘矩阵的第二个中括号,代表着矩阵维度2。
第二个括号为之前相乘矩阵的第二个中括号,代表着矩阵维度2。
这样前面两个维度就很好地确定下来了,由此可以总结出相应的规律:前面的维度由第一个矩阵确定,后面的维度由第二个矩阵确定。
3.matmul乘法的研究。
上文有提到过tf.matmul与np.dot函数的操作类似,是关于矩阵的乘法操作,首先这里使用几个小程序感受一下tf.matmul()函数的操作:
import numpy as np
import tensorflow as tf
x = np.array([[[1,2,3],[4,5,6]]])
y = np.array([[[1,2],[3,4],[5,6]]])
tranpose_y = tf.transpose(y)
results = tf.matmul(x,y)
print(results)
x.shape = (1,2,3),y.shape = (1,3,2),此时得到的结果正是正常矩阵相乘的结果
 但是如果使用两个相同的矩阵使用transpose_b = True操作完成之后
但是如果使用两个相同的矩阵使用transpose_b = True操作完成之后
x = np.array([[[1,2,3],[4,5,6]]])
y = np.array([[[1,2,3],[4,5,6]]])
results = tf.matmul(x,y,transpose_b = True)
print('results = ')
print(results)
 transpose_a:如果True,a在乘法之前转置
transpose_a:如果True,a在乘法之前转置
transpose_b:如果True,b在乘法之前转置
1.如果transpose_b参数设置为False,那么x的最后一维要跟y的倒数第二维相等,即
tf.matmul(x,y,transpose_b = False)
x.shape = [...,x1,x2]
y.shape = [...,y1,y2]
x2 = y1
2.如果transpose_b参数设置为True,那么x的最后一维要跟y的最后一维相等,transpose_b = True
tf.matmul(x,y,transpose_b = True)
x.shape = [...,x1,x2]
y.shape = [...,y1,y2]
x2 = y2






















 8269
8269











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








