模拟退火算法从某一较高的温度出发,这个温度称为初始温度,伴随着温度参数的不断下降,算法中的解趋于稳定,但是,可能这样的稳定解是一个局部最优解,此时,模拟退火算法中会以一定的概率跳出这样的局部最优解,以寻找目标函数的全局最优解。如上图中所示,若此时寻找到了A点处的解,模拟退火算法会以一定的概率跳出这个解,如跳到了D点重新寻找,这样在一定程度上增加了寻找到全局最优解的可能性。
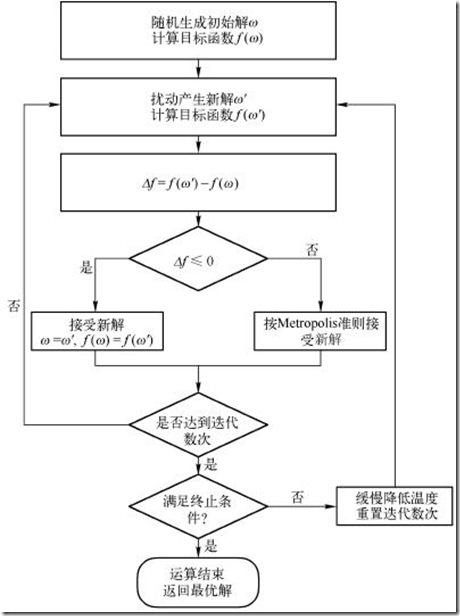
模拟退火算法流程
模拟退火算法C++实现
//simulated annealing
//F(x) = 6x^7+8x^6+7x^3+5x^2-xy
//x在0~100之间,输入y,求F最小值
#include <iostream>
#include <time.h>
#include <math.h>
#define ITERS 10 //迭代次数
#define T 100 //温度上界
#define Tmin 1e-8 //温度下界
#define delta 0.98
#define INF 1e99 //double范围正负1.7e308
using namespace std;
double random()
{
double a = rand()*1.0 / RAND_MAX; //随机数生成在0~1之间
if (rand() & 1) //x&1结果不是0就是1
a *= -1; //结果在-1~1之间
return a;
}
double F(double x, double y)
{
return 6 * pow(x, 7) + 8 * pow(x, 6) + 7 * pow(x, 3) + 5 * pow(x, 2) - x*y;
}
double SA(double y)
{
double result = INF;
double result_new = INF;
double t = T;
srand(time(NULL));
double x[ITERS];
for (int i = 0; i < ITERS; i++)
x[i] = fabs(random()) * 100; //初始化数组
while (t>Tmin)
{
for (int i = 0; i < ITERS; i++)
{
result = F(x[i], y); //计算目标函数
double x_new = x[i] + random()*t; //扰动在邻域内产生新解
if (x_new>=0 && x_new<=100)
{
result_new = F(x_new, y); //新解的目标函数值
if (result_new - result < 0)
{
x[i] = x_new; //一定接受下降
}
else
{
double p = exp(-(result_new - result) / t);
if (fabs(random()) < p)
x[i] = x_new; //以概率接受新解
}
}
}
t *= delta;
}
for (int i = 0; i < ITERS; i++)
{
if (result > F(x[i], y))
result = F(x[i], y);
}
return result;
}
int main()
{
double y;
cout << "input y:";
cin >> y;
cout << endl;
cout << "result: " << SA(y) << endl;
return 0;
}




















 675
675

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








