【CFD理论】扩散项-02
- 非正交修正
- 非正交 non orthogonal
- skewness和non-orthogonal的区别
- 三种分解方法:
- minimum correction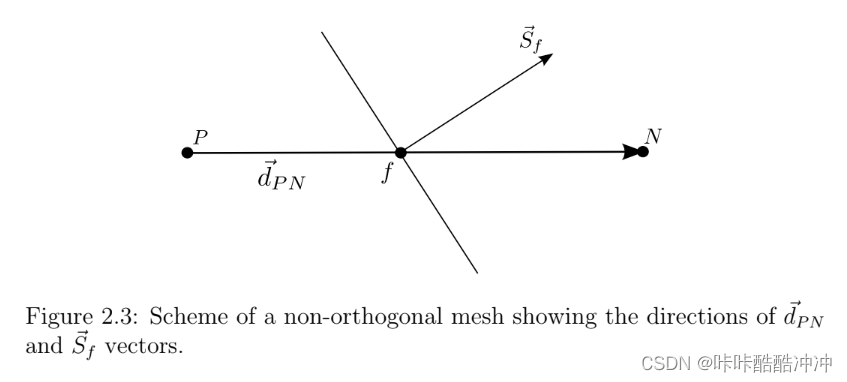
- orthogonal correction approach
- over-relaxed approach
- Algebraic Equation for Non-orthogonal Meshes
- Example 2
- bondary conditions for non-orthogonal grids
- skewness
- under relaxation
- 【补充内容】Fluid Mechanics 101- non-orthogonal corrector2
非正交修正
最小修正(minimum correction)
正交修正(orthogonal correction)
超松弛 (over-relaxed)
非正交 non orthogonal
扩散项有限体积法回顾:
∫
V
(
∇
⋅
(
D
∇
ϕ
)
+
Q
)
d
V
=
0
⇒
∑
f
∫
f
D
∇
ϕ
⋅
d
S
+
Q
p
V
p
=
0
⇒
∑
f
D
(
∇
ϕ
)
f
⋅
S
f
+
Q
p
V
P
=
0
\begin{aligned} & \int_V (\nabla \cdot (D\nabla\phi)+Q)dV=0\\ &\Rightarrow \sum_f \int_f D\nabla \phi \cdot d\boldsymbol S+Q_pV_p=0\\ &\Rightarrow \sum_f D(\nabla \phi)_f \cdot \boldsymbol S_f+Q_pV_P=0 \end{aligned}
∫V(∇⋅(D∇ϕ)+Q)dV=0⇒f∑∫fD∇ϕ⋅dS+QpVp=0⇒f∑D(∇ϕ)f⋅Sf+QpVP=0
skewness和non-orthogonal的区别

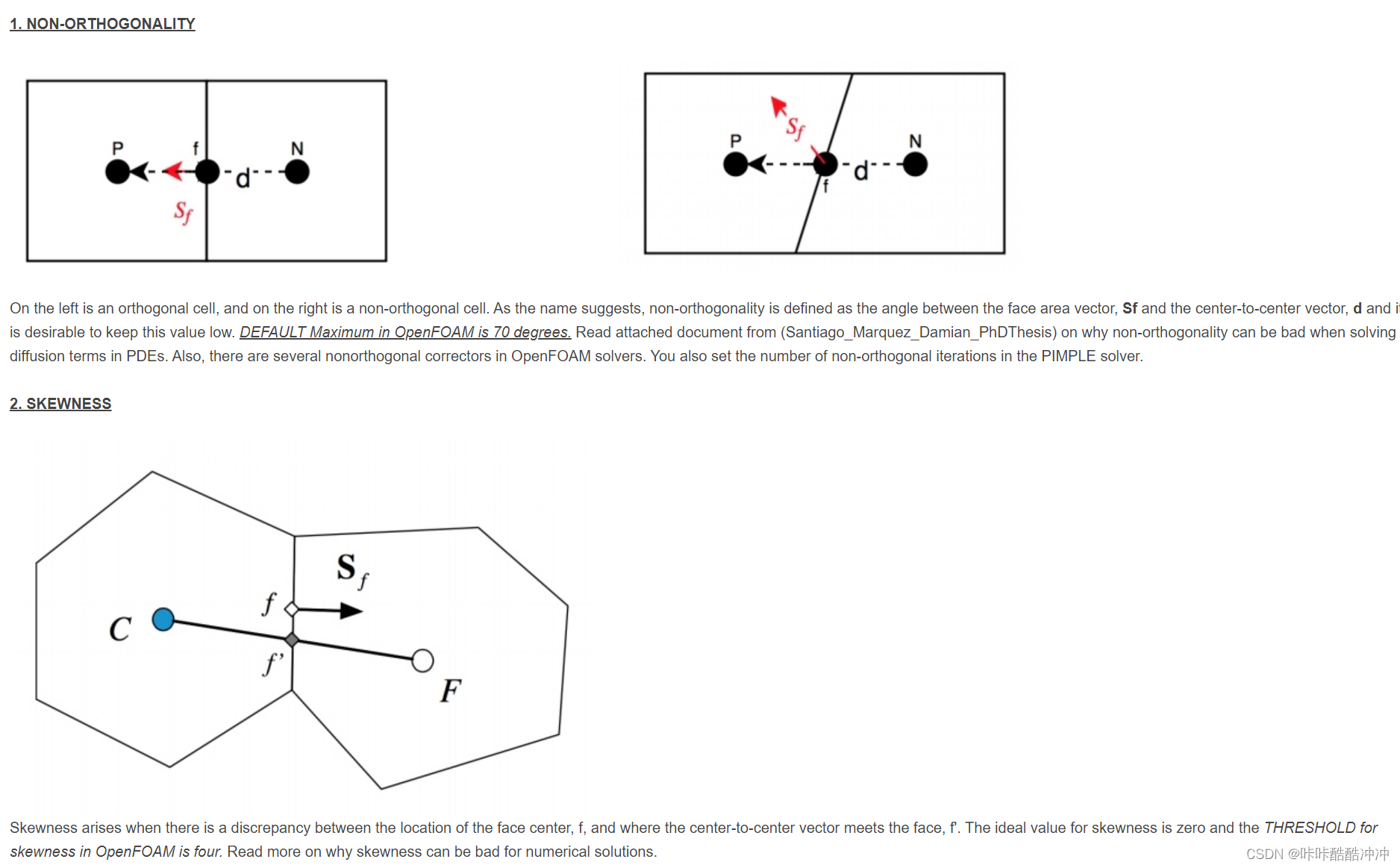
网格正交的扩散项
(
∇
ϕ
)
⋅
S
f
⃗
=
∣
S
f
⃗
∣
(
ϕ
N
−
ϕ
P
)
∣
d
P
N
⃗
∣
(\nabla\phi)\cdot \vec{S_f}=\frac{\left|\vec{S_f}\right|(\phi_N-\phi_P)}{\left|\vec{d_{PN}}\right|}
(∇ϕ)⋅Sf=∣
∣dPN∣
∣∣
∣Sf∣
∣(ϕN−ϕP)
三种分解方法:
- 最小修正(minimum correction)
- 正交修正(orthogonal correction)
- 超松弛(over-relaxed)
minimum correction
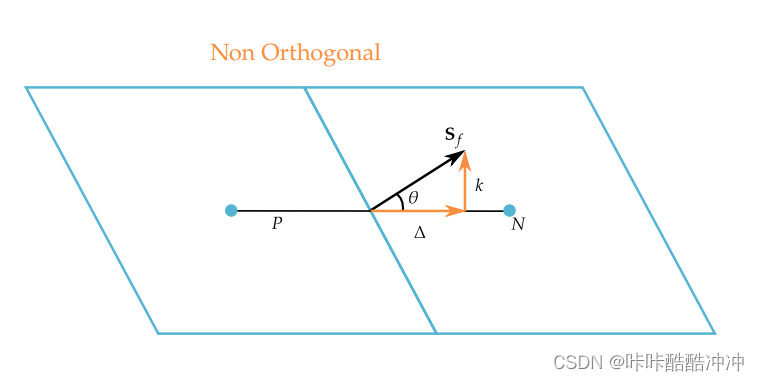
S
f
=
Δ
⃗
+
k
⃗
Δ
⃗
=
∣
S
⃗
f
∣
⋅
c
o
s
θ
⋅
P
N
⃗
∣
P
N
∣
(
∇
ϕ
)
f
⋅
S
f
=
(
∇
ϕ
)
f
⋅
Δ
+
(
Δ
ϕ
)
f
⋅
k
\begin{aligned} & \boldsymbol S_f=\vec \Delta + \vec k \\ & \vec \Delta=\left| \vec S_f\right|\cdot cos \theta \cdot \frac{\vec {PN}}{\left | PN\right |}\\ &(\nabla \phi)_f \cdot \boldsymbol S_f\\ &=(\nabla\phi)_f\cdot \Delta+(\Delta \phi)_f\cdot \boldsymbol k\\ &\\ \end{aligned}
Sf=Δ+kΔ=∣
∣Sf∣
∣⋅cosθ⋅∣PN∣PN(∇ϕ)f⋅Sf=(∇ϕ)f⋅Δ+(Δϕ)f⋅k
orthogonal correction approach
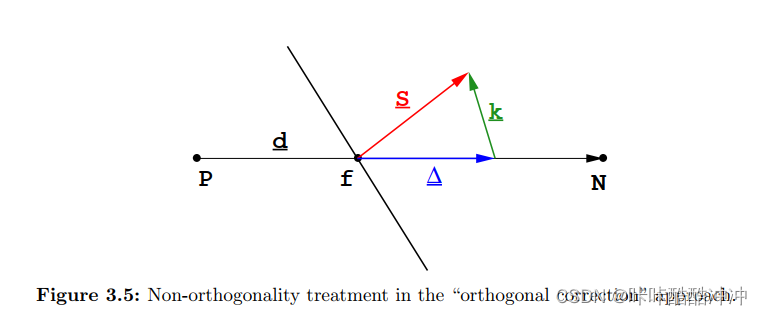
S
f
=
Δ
⃗
+
k
⃗
Δ
⃗
=
∣
S
⃗
f
∣
⋅
P
N
⃗
∣
P
N
∣
(
∇
ϕ
)
f
⋅
S
f
=
(
∇
ϕ
)
f
⋅
Δ
+
(
Δ
ϕ
)
f
⋅
k
\begin{aligned} & \boldsymbol S_f=\vec \Delta + \vec k \\ & \vec \Delta=\left| \vec S_f\right|\cdot \frac{\vec {PN}}{\left | PN\right |}\\ &(\nabla \phi)_f \cdot \boldsymbol S_f\\ &=(\nabla\phi)_f\cdot \Delta+(\Delta \phi)_f\cdot \boldsymbol k\\ &\\ \end{aligned}
Sf=Δ+kΔ=∣
∣Sf∣
∣⋅∣PN∣PN(∇ϕ)f⋅Sf=(∇ϕ)f⋅Δ+(Δϕ)f⋅k
over-relaxed approach
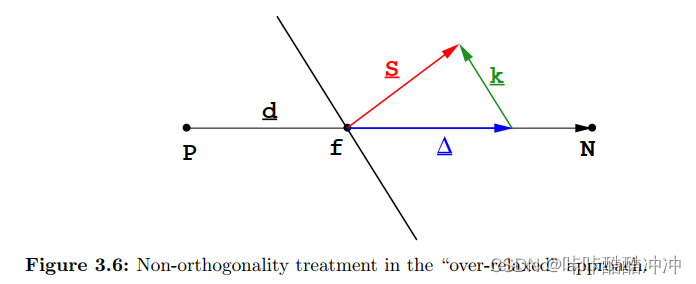
S
f
=
Δ
⃗
+
k
⃗
Δ
⃗
=
∣
S
⃗
f
∣
c
o
s
θ
⋅
P
N
⃗
∣
P
N
∣
=
P
N
⃗
∣
S
f
∣
2
S
f
⋅
P
N
⃗
(
∇
ϕ
)
f
⋅
S
f
=
(
∇
ϕ
)
f
⋅
Δ
+
(
Δ
ϕ
)
f
⋅
k
\begin{aligned} & \boldsymbol S_f=\vec \Delta + \vec k \\ & \vec \Delta=\frac{\left| \vec S_f\right|}{cos\theta}\cdot \frac{\vec {PN}}{\left | PN\right |}=\frac{ \vec{PN}\left |\boldsymbol S_f\right |^2}{\boldsymbol S_f \cdot \vec{PN}}\\ &(\nabla \phi)_f \cdot \boldsymbol S_f\\ &=(\nabla\phi)_f\cdot \Delta+(\Delta \phi)_f\cdot \boldsymbol k\\ &\\ \end{aligned}
Sf=Δ+kΔ=cosθ∣
∣Sf∣
∣⋅∣PN∣PN=Sf⋅PNPN∣Sf∣2(∇ϕ)f⋅Sf=(∇ϕ)f⋅Δ+(Δϕ)f⋅k
Algebraic Equation for Non-orthogonal Meshes
∑
f
(
D
∇
ϕ
)
⋅
S
f
=
∑
f
(
(
D
∇
ϕ
)
f
⋅
(
Δ
+
k
)
)
=
∑
f
(
D
∇
ϕ
)
f
⋅
Δ
+
∑
f
(
D
∇
ϕ
)
f
⋅
k
=
∑
f
(
D
ϕ
N
−
ϕ
P
P
N
)
∣
Δ
∣
+
∑
f
(
D
∇
ϕ
)
⋅
k
\begin{aligned} & \sum_f (D\nabla \phi)\cdot\boldsymbol S_f=\sum _f((D\nabla \phi)_f\cdot (\Delta+\boldsymbol k))\\ & =\sum_f(D\nabla \phi)_f\cdot\Delta+\sum_f(D\nabla \phi)_f\cdot\boldsymbol k \\ & =\sum_f(D\frac{\phi_N-\phi_P}{PN})\left|\Delta\right|+\sum_f(D\nabla\phi)\cdot \boldsymbol k \end{aligned}
f∑(D∇ϕ)⋅Sf=f∑((D∇ϕ)f⋅(Δ+k))=f∑(D∇ϕ)f⋅Δ+f∑(D∇ϕ)f⋅k=f∑(DPNϕN−ϕP)∣Δ∣+f∑(D∇ϕ)⋅k
a
N
=
D
P
N
∣
Δ
∣
f
a
P
=
∑
f
D
P
N
∣
Δ
∣
f
b
P
=
S
P
V
P
+
∑
f
(
D
∇
ϕ
)
⋅
k
a
p
ϕ
p
+
∑
f
a
N
ϕ
N
=
b
P
\begin{aligned} & a_N=\frac{D}{PN}\left|\Delta\right|_f\\ & a_P=\sum_f \frac{D}{PN}\left|\Delta\right|_f\\ & b_P=S_PV_P+\sum_f(D\nabla\phi)\cdot \boldsymbol k\\ & a_p\phi_p+\sum_f a_N\phi_N=b_P \end{aligned}
aN=PND∣Δ∣faP=f∑PND∣Δ∣fbP=SPVP+f∑(D∇ϕ)⋅kapϕp+f∑aNϕN=bP
Example 2
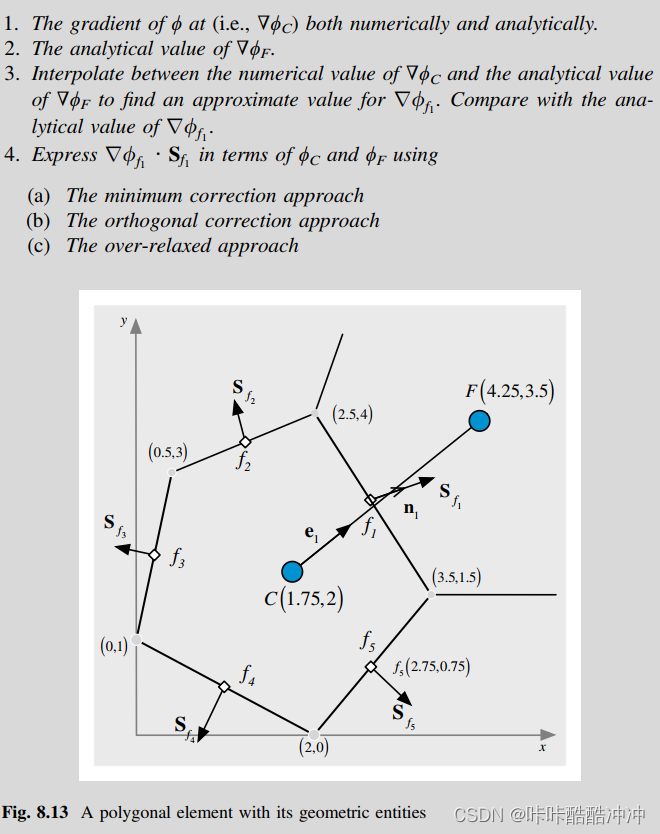
1.
ϕ
=
x
2
+
y
2
+
x
2
y
2
∇
ϕ
=
∂
ϕ
∂
x
i
+
∂
ϕ
∂
y
j
=
(
2
x
+
2
x
y
2
)
i
+
(
2
y
+
2
x
2
y
)
j
C
(
1.75
,
2
)
a
n
a
l
y
t
i
c
a
l
v
a
l
u
e
:
∇
ϕ
C
=
(
2
∗
1.75
+
2
∗
1.75
∗
2
2
)
i
+
(
2
∗
2
+
2
∗
2
∗
1.7
5
2
)
j
=
17.5
i
+
16.25
j
n
u
m
e
r
i
c
a
l
v
a
l
u
e
:
∇
ϕ
C
=
1
V
C
∑
f
ϕ
f
S
f
=
1
8.625
[
84.625
(
2.5
i
+
j
)
+
42.0625
(
−
i
+
2
j
)
+
4.3125
(
−
2
i
+
0.5
j
)
+
1.5
(
−
i
+
2
j
)
+
12.37890625
(
1.5
i
−
1.5
j
)
]
=
20.63111
i
+
17.31454
j
\begin{aligned} & \phi=x^2+y^2+x^2y^2\\ & \nabla \phi=\frac{\partial \phi}{\partial x}\boldsymbol i+ \frac{\partial \phi}{\partial y}\boldsymbol j=(2x+2xy^2)\boldsymbol i+(2y+2x^2y)\boldsymbol j\\ & C(1.75,2)\\ & analytical\ value:\\ & \nabla \phi_C= (2*1.75+2*1.75*2^2)\boldsymbol i +(2*2+2*2*1.75^2)\boldsymbol j=17.5\boldsymbol i +16.25\boldsymbol j\\ & numerical \ value:\\ & \nabla\phi_C=\frac{1}{V_C}\sum_f\phi_f\boldsymbol S_f\\ & =\frac{1}{8.625}\left[ 84.625(2.5\boldsymbol i+\boldsymbol j)+ 42.0625(- \boldsymbol i+2\boldsymbol j)+ 4.3125(- 2\boldsymbol i+0.5\boldsymbol j)+ 1.5(- \boldsymbol i+2\boldsymbol j)+ 12.37890625(1.5\boldsymbol i-1.5\boldsymbol j) \right]\\ & =20.63111\boldsymbol i+17.31454\boldsymbol j\\ \end{aligned}
ϕ=x2+y2+x2y2∇ϕ=∂x∂ϕi+∂y∂ϕj=(2x+2xy2)i+(2y+2x2y)jC(1.75,2)analytical value:∇ϕC=(2∗1.75+2∗1.75∗22)i+(2∗2+2∗2∗1.752)j=17.5i+16.25jnumerical value:∇ϕC=VC1f∑ϕfSf=8.6251[84.625(2.5i+j)+42.0625(−i+2j)+4.3125(−2i+0.5j)+1.5(−i+2j)+12.37890625(1.5i−1.5j)]=20.63111i+17.31454j
∇ ϕ F = 112.625 i + 133.4375 j \begin{aligned} & \nabla \phi_F=112.625\boldsymbol i+133.4375\boldsymbol j\\ \end{aligned} ∇ϕF=112.625i+133.4375j
插值
∇
ϕ
f
1
\nabla \phi_{f1}
∇ϕf1:
∇
ϕ
f
1
=
g
f
1
∇
ϕ
F
+
(
1
−
g
f
1
)
∇
ϕ
C
\nabla \phi_{f1}=g_{f1}\nabla \phi_F+(1-g_{f1})\nabla \phi_C
∇ϕf1=gf1∇ϕF+(1−gf1)∇ϕC
∇
ϕ
F
=
112.625
i
+
133.4375
j
\nabla \phi_F=112.625\boldsymbol i+133.4375\boldsymbol j
∇ϕF=112.625i+133.4375j
numerical value of the gradient at C:
∇
ϕ
C
=
20.63111
i
+
17.31454
j
\nabla \phi_C=20.63111\boldsymbol i+17.31454\boldsymbol j
∇ϕC=20.63111i+17.31454j
g
f
1
=
d
C
f
1
d
C
f
1
+
d
f
1
F
=
0.5
g_{f1}=\frac{d_{Cf1}}{d_{Cf1}+d_{f1F}}=0.5
gf1=dCf1+df1FdCf1=0.5
numerical value:
∇
ϕ
f
1
=
66.628055
i
+
75.37602
j
\nabla \phi_{f1}=66.628055\boldsymbol i+75.37602\boldsymbol j
∇ϕf1=66.628055i+75.37602j
analytical value:
f
1
(
3
,
2.75
)
f_1(3,2.75)
f1(3,2.75)
∇
ϕ
f
1
=
(
2
x
+
2
x
y
2
)
i
+
(
2
y
+
2
y
x
2
)
j
\nabla \phi_{f1}=(2x+2xy^2)\boldsymbol i +(2y+2yx^2)\boldsymbol j
∇ϕf1=(2x+2xy2)i+(2y+2yx2)j
∇
ϕ
f
1
=
51.375
i
+
55
j
\nabla \phi_{f1}=51.375\boldsymbol i +55\boldsymbol j
∇ϕf1=51.375i+55j
−
∇
ϕ
f
1
⋅
S
f
1
=
E
f
1
ϕ
C
−
ϕ
F
d
C
F
−
∇
ϕ
f
1
⋅
T
f
1
-\nabla \phi_{f1}\cdot\boldsymbol S_{f1}=E_{f1}\frac{\phi_C-\phi_F}{d_{CF}}-\nabla \phi_{f1}\cdot \boldsymbol T_{f1}
−∇ϕf1⋅Sf1=Ef1dCFϕC−ϕF−∇ϕf1⋅Tf1
S
f
1
=
2.5
i
+
j
\boldsymbol S_{f1}=2.5\boldsymbol i+\boldsymbol j
Sf1=2.5i+j
e
1
=
d
C
F
d
C
F
=
0.8575
i
+
0.51445
j
\boldsymbol e_1=\frac{\boldsymbol d_{CF}}{d_{CF}}=0.8575\boldsymbol i+0.51445\boldsymbol j
e1=dCFdCF=0.8575i+0.51445j
(a) minimum correction approach
E
f
1
=
(
e
1
⋅
S
f
1
)
e
1
=
2.279
i
+
1.368
j
⇒
E
f
1
=
2.658
\boldsymbol E_{f1}=(\boldsymbol e_1\cdot\boldsymbol S_{f1})\boldsymbol e_1=2.279\boldsymbol i+1.368\boldsymbol j \Rightarrow \boldsymbol E_{f1}=2.658
Ef1=(e1⋅Sf1)e1=2.279i+1.368j⇒Ef1=2.658
T
f
1
=
S
f
1
−
E
f
1
=
0.221
i
−
0.368
j
⇒
∇
ϕ
f
1
⋅
T
f
1
=
(
66.628055
i
+
75.37602
j
)
⋅
(
0.221
i
−
0.368
j
)
=
−
13.014
\boldsymbol T_{f1}=\boldsymbol S_{f1}-\boldsymbol E_{f1}=0.221\boldsymbol i-0.368\boldsymbol j \Rightarrow \nabla \phi_{f1} \cdot \boldsymbol T_{f1}=(66.628055\boldsymbol i+75.37602\boldsymbol j)\cdot (0.221\boldsymbol i-0.368\boldsymbol j)=-13.014
Tf1=Sf1−Ef1=0.221i−0.368j⇒∇ϕf1⋅Tf1=(66.628055i+75.37602j)⋅(0.221i−0.368j)=−13.014
−
∇
ϕ
f
1
⋅
S
f
1
=
2.658
2.9155
(
ϕ
C
−
ϕ
F
)
+
13.014
=
0.912
(
ϕ
C
−
ϕ
F
)
+
13.014
-\nabla \phi_{f1}\cdot\boldsymbol S_{f1}=\frac{2.658}{2.9155}(\phi_C-\phi_F)+13.014=0.912(\phi_C-\phi_F)+13.014
−∇ϕf1⋅Sf1=2.91552.658(ϕC−ϕF)+13.014=0.912(ϕC−ϕF)+13.014
(b) orthogonal correction approach
E
f
1
=
e
1
⋅
S
f
1
=
2.309
i
+
1.385
j
⇒
E
f
1
=
2.693
\boldsymbol E_{f1}=\boldsymbol e_1\cdot\boldsymbol S_{f1}=2.309\boldsymbol i+1.385\boldsymbol j \Rightarrow \boldsymbol E_{f1}=2.693
Ef1=e1⋅Sf1=2.309i+1.385j⇒Ef1=2.693
T
f
1
=
S
f
1
−
E
f
1
=
0.191
i
−
0.385
j
⇒
∇
ϕ
f
1
⋅
T
f
1
=
(
66.628055
i
+
75.37602
j
)
⋅
(
0.191
i
−
0.385
j
)
=
−
16.294
\boldsymbol T_{f1}=\boldsymbol S_{f1}-\boldsymbol E_{f1}=0.191\boldsymbol i-0.385\boldsymbol j \Rightarrow \nabla \phi_{f1} \cdot \boldsymbol T_{f1}=(66.628055\boldsymbol i+75.37602\boldsymbol j)\cdot (0.191\boldsymbol i-0.385\boldsymbol j)=-16.294
Tf1=Sf1−Ef1=0.191i−0.385j⇒∇ϕf1⋅Tf1=(66.628055i+75.37602j)⋅(0.191i−0.385j)=−16.294
−
∇
ϕ
f
1
⋅
S
f
1
=
2.693
2.9155
(
ϕ
C
−
ϕ
F
)
+
16.294
=
0.924
(
ϕ
C
−
ϕ
F
)
+
16.294
-\nabla \phi_{f1}\cdot\boldsymbol S_{f1}=\frac{2.693}{2.9155}(\phi_C-\phi_F)+16.294=0.924(\phi_C-\phi_F)+16.294
−∇ϕf1⋅Sf1=2.91552.693(ϕC−ϕF)+16.294=0.924(ϕC−ϕF)+16.294
c) over-relaxed approach
E
f
1
=
S
1
⋅
S
1
e
1
⋅
S
f
1
e
1
=
2.339
i
+
1.403
j
⇒
E
f
1
=
2.728
\boldsymbol E_{f1}=\frac{\boldsymbol S_1\cdot\boldsymbol S_1}{\boldsymbol e_1\cdot\boldsymbol S_{f1}}\boldsymbol e_1=2.339\boldsymbol i+1.403\boldsymbol j \Rightarrow \boldsymbol E_{f1}=2.728
Ef1=e1⋅Sf1S1⋅S1e1=2.339i+1.403j⇒Ef1=2.728
T
f
1
=
S
f
1
−
E
f
1
=
0.161
i
−
0.403
j
⇒
∇
ϕ
f
1
⋅
T
f
1
=
(
66.628055
i
+
75.37602
j
)
⋅
(
0.161
i
−
0.403
j
)
=
−
19.649
\boldsymbol T_{f1}=\boldsymbol S_{f1}-\boldsymbol E_{f1}=0.161\boldsymbol i-0.403\boldsymbol j \Rightarrow \nabla \phi_{f1} \cdot \boldsymbol T_{f1}=(66.628055\boldsymbol i+75.37602\boldsymbol j)\cdot (0.161\boldsymbol i-0.403\boldsymbol j)=-19.649
Tf1=Sf1−Ef1=0.161i−0.403j⇒∇ϕf1⋅Tf1=(66.628055i+75.37602j)⋅(0.161i−0.403j)=−19.649
−
∇
ϕ
f
1
⋅
S
f
1
=
2.728
2.9155
(
ϕ
C
−
ϕ
F
)
+
16.294
=
0.936
(
ϕ
C
−
ϕ
F
)
+
19.649
-\nabla \phi_{f1}\cdot\boldsymbol S_{f1}=\frac{2.728}{2.9155}(\phi_C-\phi_F)+16.294=0.936(\phi_C-\phi_F)+19.649
−∇ϕf1⋅Sf1=2.91552.728(ϕC−ϕF)+16.294=0.936(ϕC−ϕF)+19.649
bondary conditions for non-orthogonal grids
dirichlet boundary condition
neumann boundary condition
mixed boundary condition
skewness
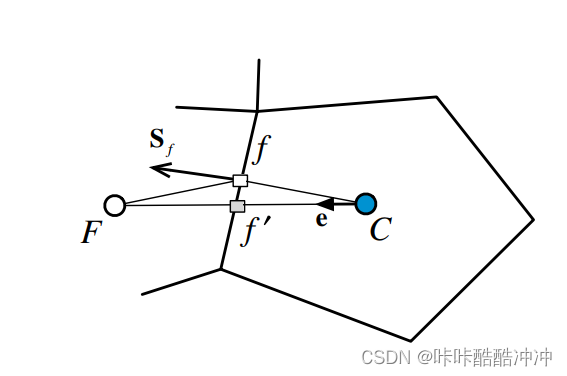
ϕ
f
=
ϕ
f
′
+
(
∇
ϕ
)
f
′
⋅
d
f
′
f
\phi_f=\phi_{f'}+(\nabla \phi)_{f'}\cdot \boldsymbol d_{f'f}
ϕf=ϕf′+(∇ϕ)f′⋅df′f
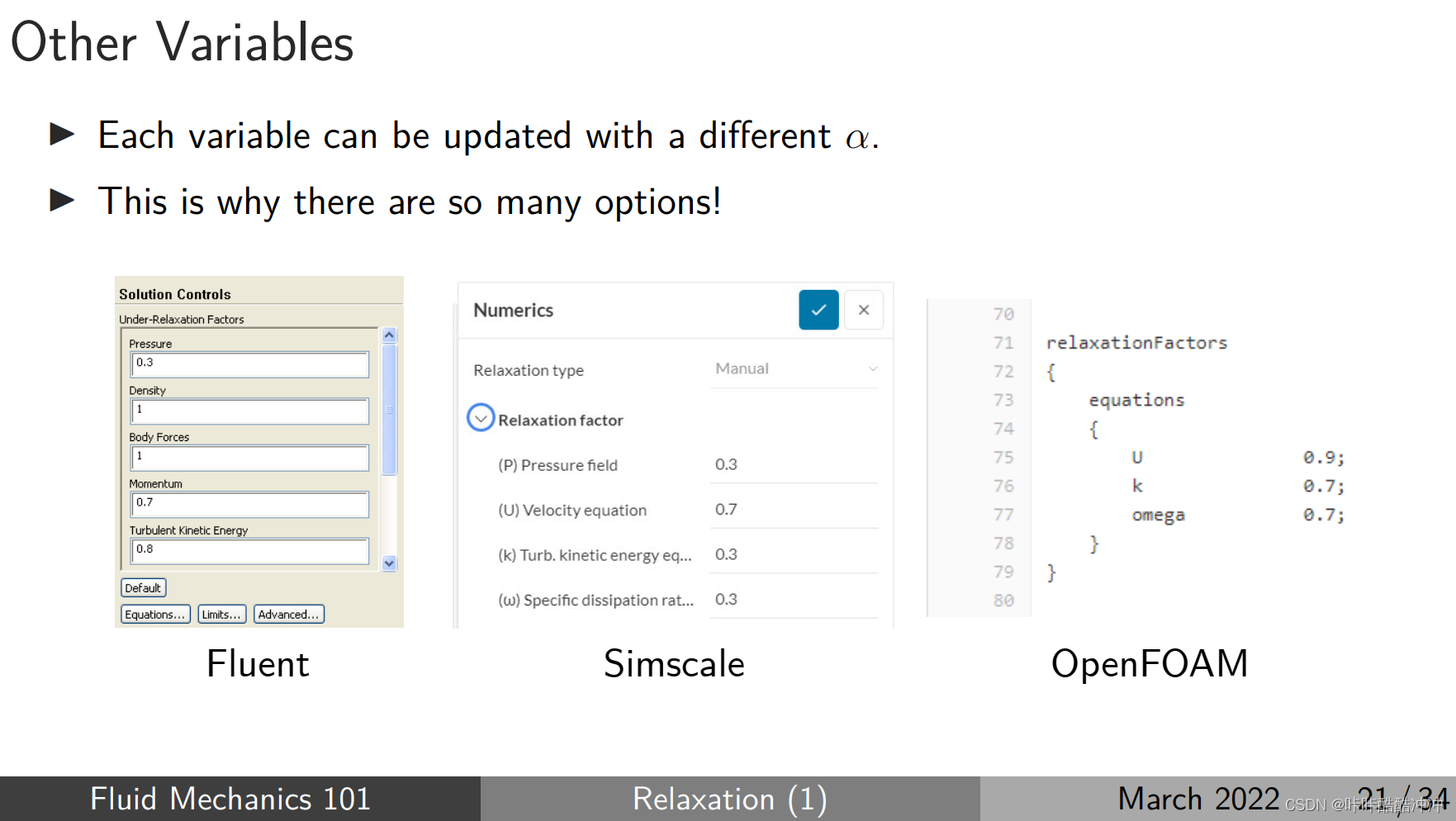
under relaxation
a
C
ϕ
C
+
∑
f
a
N
ϕ
N
=
b
P
a_C\phi_C+\sum_f a_N\phi_N=b_P
aCϕC+∑faNϕN=bP
ϕ
p
=
b
P
−
∑
f
a
N
ϕ
N
a
P
\phi_p=\frac{b_P-\sum_f a_N\phi_N}{a_P}
ϕp=aPbP−∑faNϕN
显式:
ϕ
P
=
ϕ
P
o
l
d
+
α
(
b
p
−
∑
f
a
N
ϕ
N
a
P
−
ϕ
P
o
l
d
)
\phi_P=\phi_P^{old}+\alpha(\frac{b_p-\sum_f a_N\phi_N}{a_P}-\phi_P^{old})
ϕP=ϕPold+α(aPbp−∑faNϕN−ϕPold)
fields p 0.3
隐式:
a
P
α
+
∑
f
a
N
ϕ
N
=
b
P
+
(
1
−
α
)
a
p
α
ϕ
p
o
l
d
\frac{a_P}{\alpha}+\sum_f a_N\phi_N=b_P+\frac{(1-\alpha)a_p}{\alpha}\phi_p^{old}
αaP+∑faNϕN=bP+α(1−α)apϕpold
equations U 0.9
[CFD] Relaxation in CFD (Part 1) - Explicit Relaxation, Under-Relaxation Factor






















 4539
4539











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








