基本对流格式
练习:
Divergence scheme example

Divergence schemes
∇ ⋅ Q \nabla \cdot Q ∇⋅Q
- 如果Q是矢量,等式可以写成:
∇ ⋅ Q = ∂ Q x ∂ x + ∂ Q y ∂ y + ∂ Q z ∂ z \nabla\cdot Q=\frac{\partial Q_x}{\partial x}+\frac{\partial Q_y}{\partial y}+\frac{\partial Q_z}{\partial z} ∇⋅Q=∂x∂Qx+∂y∂Qy+∂z∂Qz
divSchemes
{
default none;
div(Q) Gauss <interpolation scheme>;
}
- 对于对流项的典型使用,传输一个属性Q,在速度场的影响 ϕ \phi ϕ,特别的定义:
divSchemes
{
default none;
div(phi,Q) Gauss <interpolation scheme>;
}
ϕ \phi ϕ 这个关键词典型的用于代表通量(流)穿过cell面,例如
- 体积通量: ϕ = u f ⋅ S f \phi=\boldsymbol u_f \cdot \boldsymbol S_f ϕ=uf⋅Sf
- 质量通量: ϕ = ρ f ( u f ⋅ S f ) \phi=\rho_f(\boldsymbol u_f\cdot \boldsymbol S_f) ϕ=ρf(uf⋅Sf)
- 一阶
- 有界
- 面心值是根据上游值来确定
ϕ f = ϕ c \phi_f=\phi_c ϕf=ϕc
divSchemes
{
default none;
div(phi,U) Gauss upwind;
}
- 二阶
- 无界
- 对于LES计算是很好的选择,因为低耗散
ϕ f = 0.5 ( ϕ c + ϕ d ) \phi_f=0.5(\phi_c+\phi_d) ϕf=0.5(ϕc+ϕd)
divSchemes
{
default none;
div(phi,U) Gauss linear;
}
- 迎风插值权重,用一个显式的修正基于local cell gradient
- 二阶精度
- 无界
divSchemes
{
default none;
div(phi,U) Gauss linearUpwind grad(U);
}
- 守恒定律的单调上游中心方案
- 二阶
- 无界
divSchemes
{
default none;
div(phi,U) Gauss MUSCL;
}
- 一/二阶
- 无界
divSchemes
{
default none;
div(phi,U) Gauss limitedLinear <coeff>;
}
其他参考网址:
- 6.2 Numerical schemes
- 3.16 Gradient limiting
- book-2-An Introduction to Computational Fluid Dynamics, The Finite Volume Method (chapter 5)
一维定常对流扩散方程

解析解
方程:
d
(
ρ
u
ϕ
)
d
x
=
d
x
(
Γ
d
ϕ
d
x
)
\frac{d(\rho u \phi)}{dx}=\frac{d}{x}(\Gamma \frac{d\phi}{dx})
dxd(ρuϕ)=xd(Γdxdϕ)
解析解:
ρ
u
ϕ
−
(
Γ
d
ϕ
d
x
)
=
c
\rho u \phi - (\Gamma \frac{d\phi}{dx})=c
ρuϕ−(Γdxdϕ)=c
d
ϕ
d
x
=
ρ
u
Γ
ϕ
−
c
Γ
\frac{d\phi}{dx}=\frac{\rho u}{\Gamma}\phi-\frac{c}{\Gamma}
dxdϕ=Γρuϕ−Γc
w
h
e
r
e
ϕ
=
ρ
u
Γ
ϕ
−
c
Γ
where \ \phi=\frac{\rho u}{\Gamma}\phi-\frac{c}{\Gamma}
where ϕ=Γρuϕ−Γc
d
ϕ
ϕ
=
ρ
u
Γ
d
x
⇒
ρ
u
Γ
x
+
c
3
⇒
ϕ
=
C
λ
e
ρ
u
λ
x
+
c
ρ
u
\frac{d\phi}{\phi}=\frac{\rho u}{\Gamma}dx \Rightarrow \frac{\rho u}{\Gamma}x+c_3\Rightarrow\phi=\frac{C\lambda e^{\frac{\rho u}{\lambda}x}+c}{\rho u}
ϕdϕ=Γρudx⇒Γρux+c3⇒ϕ=ρuCλeλρux+c
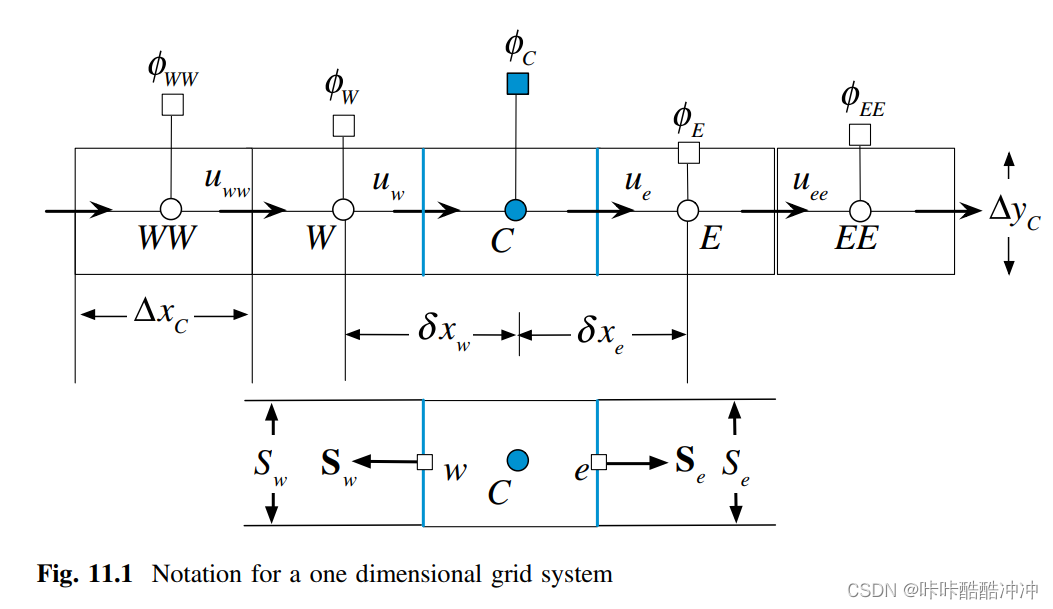
ϕ
−
ϕ
W
ϕ
E
−
ϕ
W
=
e
P
e
L
x
−
x
W
L
−
1
e
P
e
L
−
1
\frac{\phi-\phi_W}{\phi_E-\phi_W}=\frac{e^{Pe_L\frac{x-x_W}{L}}-1}{e^{Pe_L}-1}
ϕE−ϕWϕ−ϕW=ePeL−1ePeLLx−xW−1
佩克莱数 Peclet number,简称Pe数:
P
e
L
=
ρ
u
L
Γ
(
对流
/
扩散
)
,
L
=
x
E
−
x
W
Pe_L=\frac{\rho u L}{\Gamma}(对流/扩散),L=x_E-x_W
PeL=ΓρuL(对流/扩散),L=xE−xW

- 当 P e L = 0 Pe_L=0 PeL=0时,是纯扩散型
- 一般 P e L ≤ 2 Pe_L \leq 2 PeL≤2
数值解
三维 对流-扩散
∫
V
P
[
∇
⋅
(
ρ
U
ϕ
)
−
∇
⋅
(
Γ
∇
ϕ
)
]
d
V
=
0
\int_{V_P}[\nabla \cdot (\rho \boldsymbol U\phi)-\nabla\cdot(\Gamma\nabla\phi)]dV=0
∫VP[∇⋅(ρUϕ)−∇⋅(Γ∇ϕ)]dV=0
∫
V
P
[
∇
⋅
(
ρ
U
ϕ
)
−
∇
⋅
(
Γ
∇
ϕ
)
]
d
V
=
∫
∂
V
P
(
ρ
U
ϕ
−
Γ
∇
ϕ
)
⋅
d
S
=
∫
∂
V
P
[
ρ
U
ϕ
i
−
Γ
d
ϕ
d
x
i
]
⋅
d
S
=
0
\int_{V_P}[\nabla \cdot (\rho \boldsymbol U\phi)-\nabla\cdot(\Gamma\nabla\phi)]dV=\int_{\partial V_P}(\rho \boldsymbol U\phi-\Gamma \nabla \phi)\cdot d\boldsymbol S=\int_{\partial V_P}[\rho \boldsymbol U\phi \boldsymbol i-\Gamma\frac{d\phi}{dx}\boldsymbol i]\cdot d\boldsymbol S=0
∫VP[∇⋅(ρUϕ)−∇⋅(Γ∇ϕ)]dV=∫∂VP(ρUϕ−Γ∇ϕ)⋅dS=∫∂VP[ρUϕi−Γdxdϕi]⋅dS=0
- CD
- upwind
- second order upwind
Central Difference (CD) Scheme
中心差分格式

- 公式:
ϕ ( x ) = k 0 + k 1 ( x − x C ) \phi(x)=k_0+k_1(x-x_C) ϕ(x)=k0+k1(x−xC) - e处的插值格式:
ϕ e = ϕ C + ( ϕ E − ϕ C ) ( x E − x C ) ( x e − x C ) \phi_e=\phi_C+\frac{(\phi_E-\phi_C)}{(x_E-x_C)}(x_e-x_C) ϕe=ϕC+(xE−xC)(ϕE−ϕC)(xe−xC) - 均匀网格:
ϕ e = ϕ C + ϕ E 2 \phi_e=\frac{\phi_C+\phi_E}{2} ϕe=2ϕC+ϕE
数值解
对流-扩散e处插值方程
(
ρ
u
Δ
y
)
e
−
(
Γ
d
ϕ
d
x
Δ
y
)
e
=
(
ρ
u
Δ
y
)
e
ϕ
C
+
ϕ
E
2
−
(
Γ
Δ
y
δ
x
)
e
(
ϕ
E
−
ϕ
C
)
(\rho u \Delta y)_e-(\Gamma \frac{d \phi}{dx}\Delta y)_e=(\rho u \Delta y)_e\frac{\phi_C+\phi_E}{2}-(\Gamma \frac{\Delta y}{\delta x})_e(\phi_E-\phi_C)
(ρuΔy)e−(ΓdxdϕΔy)e=(ρuΔy)e2ϕC+ϕE−(ΓδxΔy)e(ϕE−ϕC)
对流-扩散w处插值方程
−
[
(
ρ
u
Δ
y
)
w
−
(
Γ
d
ϕ
d
x
Δ
y
)
w
]
=
−
[
(
ρ
u
Δ
y
)
w
ϕ
C
+
ϕ
E
2
−
(
Γ
Δ
y
δ
x
)
w
(
ϕ
C
−
ϕ
W
)
]
-[(\rho u \Delta y)_w-(\Gamma \frac{d \phi}{dx}\Delta y)_w]=-[(\rho u \Delta y)_w\frac{\phi_C+\phi_E}{2}-(\Gamma \frac{\Delta y}{\delta x})_w(\phi_C-\phi_W)]
−[(ρuΔy)w−(ΓdxdϕΔy)w]=−[(ρuΔy)w2ϕC+ϕE−(ΓδxΔy)w(ϕC−ϕW)]
∵
[
(
ρ
u
Δ
y
)
e
−
(
Γ
d
ϕ
d
x
Δ
y
)
e
]
−
[
(
ρ
u
Δ
y
)
w
−
(
Γ
d
ϕ
d
x
Δ
y
)
w
]
=
0
\because [(\rho u \Delta y)_e-(\Gamma \frac{d \phi}{dx}\Delta y)_e]-[(\rho u \Delta y)_w-(\Gamma \frac{d \phi}{dx}\Delta y)_w]=0
∵[(ρuΔy)e−(ΓdxdϕΔy)e]−[(ρuΔy)w−(ΓdxdϕΔy)w]=0
∴
[
(
ρ
u
Δ
y
)
e
−
(
Γ
d
ϕ
d
x
Δ
y
)
e
]
=
[
(
ρ
u
Δ
y
)
w
−
(
Γ
d
ϕ
d
x
Δ
y
)
w
]
(
(
ρ
u
Δ
y
)
e
2
+
Γ
e
Δ
y
e
δ
x
e
)
+
[
(
(
ρ
u
Δ
y
)
w
2
+
Γ
w
Δ
y
w
δ
x
w
)
]
ϕ
C
+
[
(
ρ
u
Δ
y
)
e
2
−
Γ
e
Δ
y
e
δ
x
e
]
ϕ
E
+
[
(
ρ
u
Δ
y
)
w
2
−
Γ
w
Δ
y
w
δ
x
w
]
ϕ
W
=
0
(
ρ
u
Δ
y
)
e
2
−
Γ
e
Δ
y
e
δ
x
e
>
0
⇒
P
e
=
(
ρ
u
)
e
δ
x
e
Γ
e
>
2
\therefore [(\rho u \Delta y)_e-(\Gamma \frac{d \phi}{dx}\Delta y)_e]=[(\rho u \Delta y)_w-(\Gamma \frac{d \phi}{dx}\Delta y)_w]\\ (\frac{(\rho u \Delta y)_e}{2}+\Gamma_e\frac{\Delta y_e}{\delta x_e})+[(\frac{(\rho u \Delta y)_w}{2}+\Gamma_w\frac{\Delta y_w}{\delta x_w})]\phi_C+[\frac{(\rho u \Delta y)_e}{2}-\Gamma_e\frac{\Delta y_e}{\delta x_e}]\phi_E+[\frac{(\rho u \Delta y)_w}{2}-\Gamma_w\frac{\Delta y_w}{\delta x_w}]\phi_W=0\\ \frac{(\rho u \Delta y)_e}{2}-\Gamma_e\frac{\Delta y_e}{\delta x_e}\gt0\\ \Rightarrow Pe=\frac{(\rho u)_e\delta x_e}{\Gamma_e}\gt2
∴[(ρuΔy)e−(ΓdxdϕΔy)e]=[(ρuΔy)w−(ΓdxdϕΔy)w](2(ρuΔy)e+ΓeδxeΔye)+[(2(ρuΔy)w+ΓwδxwΔyw)]ϕC+[2(ρuΔy)e−ΓeδxeΔye]ϕE+[2(ρuΔy)w−ΓwδxwΔyw]ϕW=02(ρuΔy)e−ΓeδxeΔye>0⇒Pe=Γe(ρu)eδxe>2
- 中心差分格式 → \rightarrow →容易振荡(发散)
- 为了减少邻值误差放大,通过减小网格尺寸,一般设置为 P e ≤ 2 Pe \leq 2 Pe≤2。
example 5.2


- table 5.2是绝对对角占优
- 纯扩散方程求解是对称矩阵,为什么对流-扩散方程不是对称矩阵?
- a W = D + F 2 , a E = D − F 2 a_W=D+\frac{F}{2},a_E=D-\frac{F}{2} aW=D+2F,aE=D−2F
























 5849
5849

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








