无监督学习
无监督学习算法只需要样本 x (无标签),这种算法可应用于细分市场、文本总结等应用。同时,无监督学习模块中引入了主成分分析(Principal components analysis, PCA),用于加速学习,它在可视化方面非常有效,帮助我们理解数据。
聚簇
无监督学习:引言
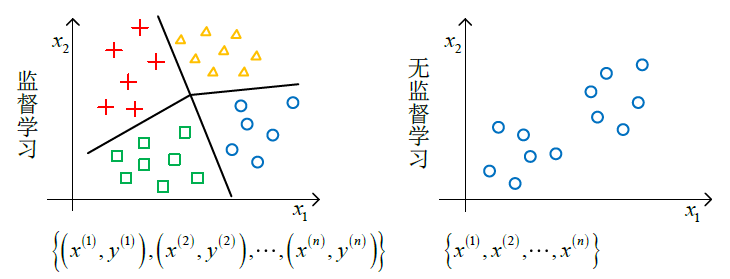
从无标签的数据中学习。
这里我们介绍一下监督学习与无监督学习的区别。
聚簇(Clustering algorithm)是无监督学习的一种方法。
聚簇的应用包含:
- 细分市场 Market segmentation
- 社会网络分析 Social network analysis
- 组织运算集群 Organize computing clusters
- 天文数据分析 Astronomical data analysis
K 均值算法
K 均值算法的目标是将有紧密关系的子集/簇聚集起来,该方法是一种迭代的方法,算法的输入是簇的个数
1 k-means 算法
x(i) 为样本点; c(i) 为 x(i) 的簇中心; μk 为簇中心
Randomly initialize
k
cluster centroids
Repeat {
for
i
= 1 to
c(i)
:= index (from 1 to
K
) of cluster centroid closest to
for
k
= 1 to
μk
:= average (mean) of points assigned to cluster
k
}
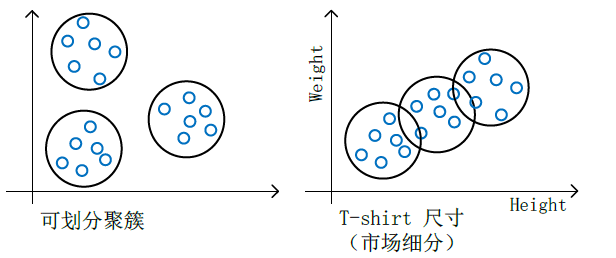
2 k-means 应对不可划分的簇
优化目标
k-means 的优化目标函数为
其中
k-meas 算法的实质是将 c(i) 与 μk 分开来求最优值,并迭代(代价递减)直至收敛。
K
均值算法的代价函数
随机初始化
一般来讲,当 K=[2,10] ,随机初始化会使得结果较好。其实质是反复地选择初始中心点,取最好的一次。随机的位置是从 x(i) 中去选,这些的效果较好。
簇数的选择
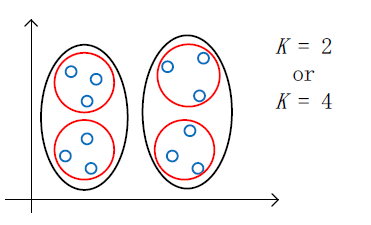
簇数的选择是一个问题,在一个目标中, K=2 or K=4 都很难说明哪个更合适,问题如下图所示。
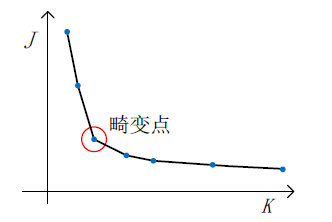
确定 K 的方法有“肘点法则”(Elbow method)、从应用出发:
- 1)“肘点法则”
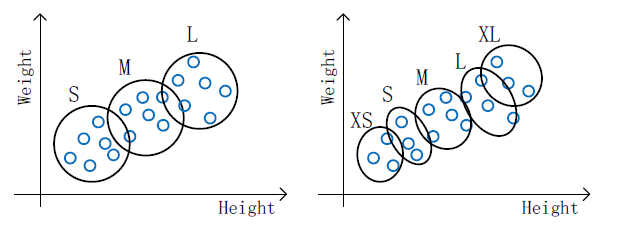
代价J 应采用“随机初始化”的方法求其最小值。 2) 从应用出发选择 K- 以 T-shirt 尺寸划分为目标,S/M/L 或 XS/S/M/L/XL 尺寸。
- 以 T-shirt 尺寸划分为目标,S/M/L 或 XS/S/M/L/XL 尺寸。
维度约减
在这一模块中,我们介绍主成分分析(Principal components analysis, PCA),应用于数据压缩(Data compression),以至于加速学习算法效率,适用于复杂数据的可视化。
维度约减是一种无监督学习,它的实质是去除冗余特征。
动机
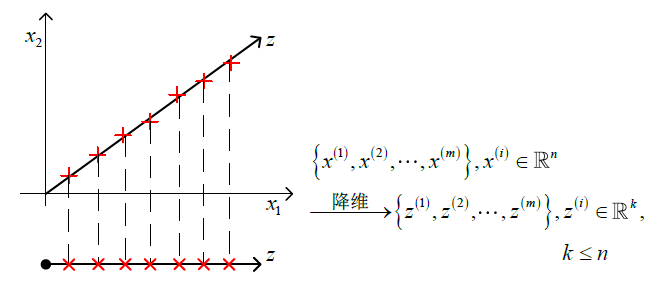
动机:数据压缩
动机:可视化
新的坐标轴与原数据有大致的对应关系。
主成分分析
主成分分析是常用的降维方法。
主成分分析的公式描述
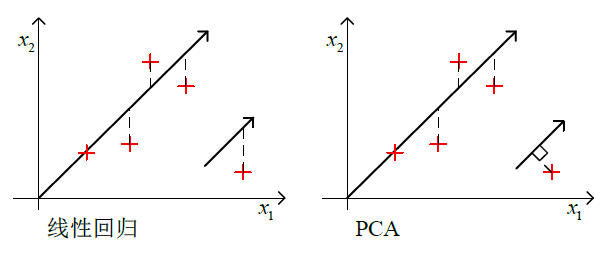
在主成分分析中,特征规范化与均值归一化是必需的。主成分分析目标的数据描述为最小化投影误差的平方,即点与投影后的对应点之间的距离的平方值最小化。
PCA 与线性回归的区别如下图所示。
主成分分析算法
PCA 执行前必须对数据集进行与处理,从而对数据进行有效地降维。
1 数据预处理
对数据做规范化处理,
当特征值的范围相差很大时,有必要做归一化处理,
2 PCA 算法
x(i)∈Rn→x(i)∈RK,K⩽n
-
1 计算
协方差矩阵
-
协方差矩阵记作Sigma(或
∑
)
Sigma=∑=1m∑i=1n(x(i))(x(i))T = 1mXTX
其中,
X=[x(1)⋯x(n)]T
2 计算协方差矩阵的
特征向量
-
通过
奇异值分解(Singular value decomposition, SVD)求
X
的特征向量。
[u, s, v] = svd(Sigma)
其中,u 为特征向量, u∈Rn×n ,
u=[u(1)⋯u(K)⋯u(n)]n×n
新的特征 z 为
z=[u(1)⋯u(K)]Tx
应用主成分分析
于压缩表达式中重构
重构是将压缩得到的特征 z ,近似重构出原来的高维特征。
同样的,
x′=[u(1)⋯u(K)]Tz
其中,
令
U=[u(1),⋯,u(n)]
,
U
为酉矩阵;记
主成分数量的选择
K
为主成分的数量,那么
- 与参数
K 相关的 2 个数值: 1 平均平方 映射误差 - 1m∑i=1m∥∥x(i)−x(i)approx∥∥2−→−目标min 2 总变差
- 1m∑i=1m∥∥x(i)∥∥2
-
降低数据存储量
加速学习算法
2) 可视化
- K=2 or K=3
- 主成分分析
http://blog.csdn.net/xiaoyu714543065/article/details/7832132 - 聚类
http://blog.csdn.net/jiang1st2010/article/details/7654120 - K 均值算法 / k-means
http://coolshell.cn/articles/7779.html - 数据降维
http://blog.csdn.net/abcjennifer/article/details/8002329 - 奇异值分解 / SVD
http://blog.csdn.net/ningyaliuhebei/article/details/7104951
使得平均平方映射误差与总变差之比小于阈值 α ,即
1m∑i=1m∣∣x(i)−x(i)approx∣∣21m∑i=1m∣∣x(i)∣∣2⩽α α=1%,5%,10%
这意味着 (1−α) 的差异被保留了。
因此,求解最优 K 值的模型为
其中, s 为奇异值分解得到的对称阵,即特征值矩阵。
应用 PCA 的建议
1 加速监督学习
经过降维处理之后,得到新的数据
(z(1),y(1)),(z(2),y(2)),⋯,(z(m),y(m))
2 PCA 的应用
-
1) 压缩
值得注意的是,PCA 不适合避免过拟合。当计算量过大,存储空间过大时,再考虑使用 PCA,PCA 不是一种提高预测准确度的方法。










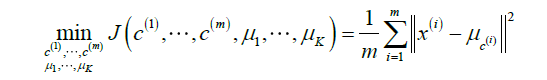














 13万+
13万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








